Comparer et optimiser les courbes ROC
Les courbes Receiver Operator Characteristic (ROC) permettent de comparer les modèles et de paramétrer le modèle sélectionné. Voyons comment et pourquoi elles sont faites.
Réglage d’un modèle
L’utilisation la plus évidente pour une courbe ROC consiste à choisir un seuil de décision qui offre les meilleures performances. Rappelez-vous que nos modèles nous fournissent des probabilités. Par exemple, il peut y avoir 65 % de chance que l’échantillon soit un randonneur. Le seuil de décision est le point au-dessus duquel un échantillon a la valeur True (randonneur) ou en dessous duquel il est assigné à la valeur false (arbre). Si notre seuil de décision était de 50 %, 65 % seraient attribués à « True » (randonneur). Toutefois, si notre seuil de décision était de 70 %, une probabilité de 65 % serait trop faible et sera attribuée à False (« arbre »).
Nous avons vu dans l’exercice précédent que lorsque nous créons une courbe ROC, nous modifions simplement le seuil de décision et évaluons le bon fonctionnement du modèle. Dans ce cas, nous pouvons trouver le seuil qui donne des résultats optimaux.
En règle générale, il n’existe pas de seuil unique qui donne le meilleur taux de vrais positifs (TPR) et un taux de faux positifs inférieur (FPR). Cela signifie que le seuil optimal dépend de ce que vous essayez d’atteindre. Par exemple, dans notre scénario, il est très important d’avoir un taux de vrais positifs élevé, car si un randonneur n’est pas identifié et qu’une avalanche se produit, l’équipe ne pourra pas le sauver. À l’inverse, si le taux de faux positifs est trop élevé, l’équipe de secours peut être envoyée à plusieurs reprises pour récupérer des personnes qui n’existent pas. Dans d’autres situations, le taux de faux positifs est considéré comme plus important. Par exemple, la science a une faible tolérance pour les résultats faux positifs. Si le taux de faux positifs des expériences scientifiques était plus élevé, il y aurait une infinité de contradictions et il serait impossible de comprendre ce qui est réel.
Comparaison des modèles avec AUC
Vous pouvez utiliser des courbes ROC pour comparer des modèles les uns aux autres, comme vous le pouvez avec les fonctions de coût. Une courbe ROC montre le bon fonctionnement d’un modèle pour différents seuils de décision. Au final, ce qui est le plus important dans un modèle est la manière dont il s’exécute dans le monde réel, où il n’y a qu’un seul seuil de décision. Alors, pourquoi comparer des modèles avec des seuils que nous n’utiliserons jamais ? Il y a deux raisons.
Tout d’abord, la comparaison des courbes ROC revient à effectuer un test statistique qui nous indique non seulement qu’un modèle était mieux adapté à cet ensemble de tests particulier, mais qu’il est susceptible de continuer à mieux fonctionner dans le futur. Cela ne fait pas partie du cadre de ce matériel d’apprentissage, mais il est important de le garder à l’esprit.
Puis, la courbe ROC indique, dans une certaine mesure, la façon dont le modèle dépend du seuil parfait. Par exemple, si notre modèle fonctionne bien uniquement lorsque nous avons un seuil de décision de 0,9, mais qu’il fonctionne très mal au-dessus ou en dessous de cette valeur, il ne s’agit pas d’une bonne conception. Nous préférerons probablement travailler avec un modèle qui fonctionne correctement pour différents seuils, sachant que si les données réelles sont légèrement différentes de notre ensemble de tests, les performances de nos modèles ne seront pas nécessairement réduites.
Comment comparer les ROC ?
La méthode la plus simple pour comparer de façon numérique les ROC est d’utiliser la zone sous la courbe (AUC). Il s’agit, littéralement, de la zone du graphique qui se trouve sous la courbe. Par exemple, notre modèle parfait du dernier exercice a une AUC de 1 :
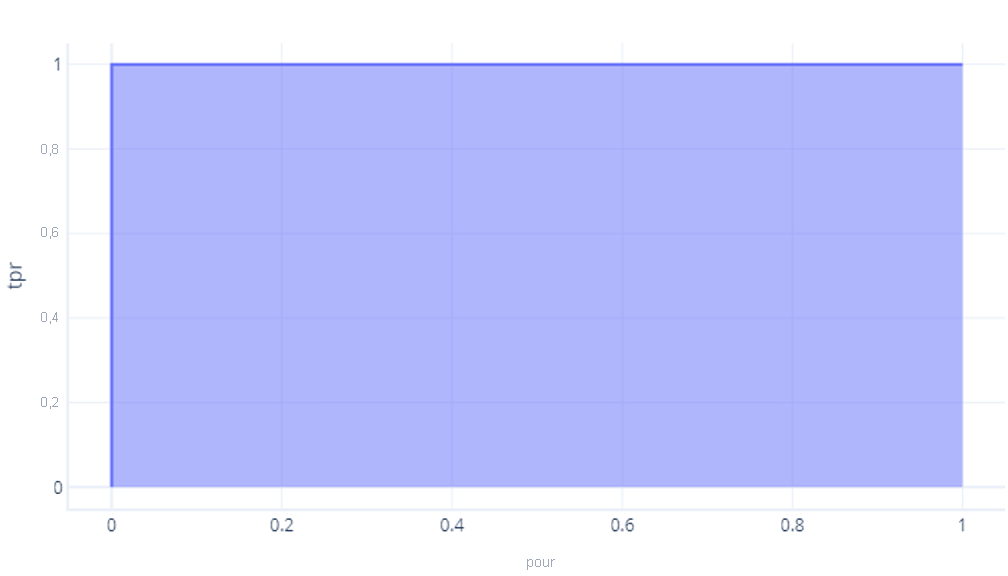
Notre modèle qui n’est pas mieux que le hasard a une zone d’environ 0,5 :
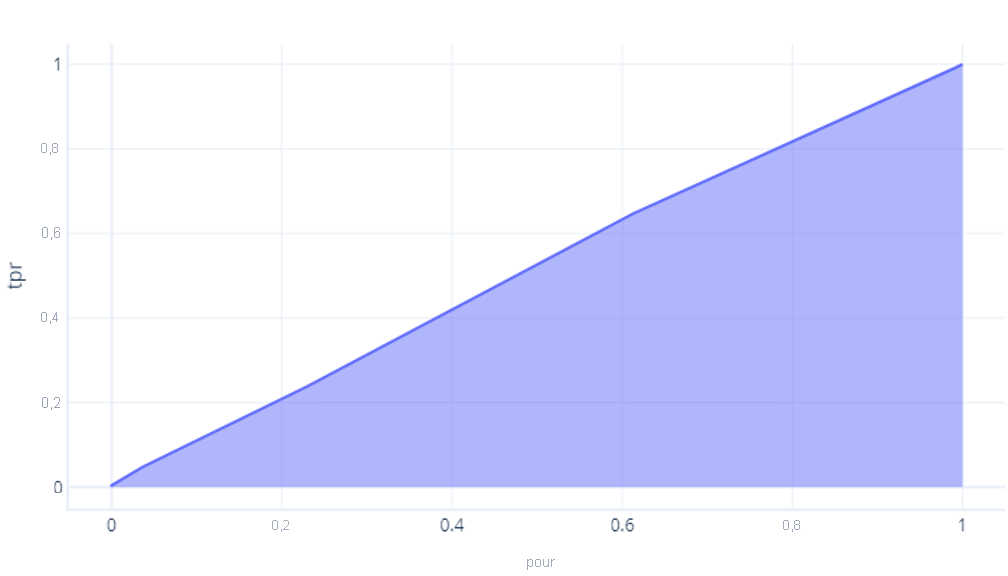
Plus le modèle est parfait, plus cette zone devient importante. Si nous avons un modèle avec une grande AUC, nous savons qu’il fonctionne bien pour divers seuils, qu’il a probablement une bonne architecture et a été formé correctement. En revanche, un modèle avec une petite AUC (plus proche de 0,5) ne fonctionne pas bien.