Déséquilibres des données

Effectué

Quand les étiquettes de nos données contiennent plus de catégories qu’une autre, on dit qu’il y a un déséquilibre des données. Par exemple, rappelez-vous que dans notre scénario, nous essayons d’identifier les objets trouvés par les capteurs des drones. Nos données sont déséquilibrées, car le nombre de randonneurs, d’animaux, d’arbres et de rochers varie considérablement dans nos données d’apprentissage. Pour ce faire, vous pouvez afficher les données en tableau :

Étiquette	Randonneur	Animal	Arborescence	Pierre
Count	400	200	800	800

Ou en le traçant :

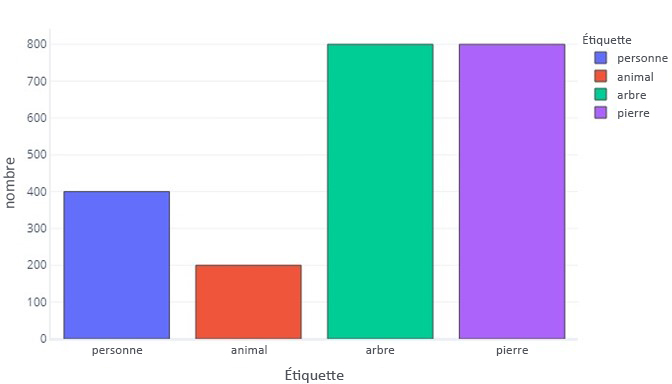
La plupart des données sont des arbres ou des roches. Un jeu de données équilibré n’a pas ce problème.

Par exemple, si nous tentions de prédire si un objet est un randonneur, un animal, un arbre ou une roche, nous voudrions un nombre égal de toutes les catégories, comme ceci :

Étiquette	Randonneur	Animal	Arborescence	Pierre
Count	550	550	550	550

Si nous tentions simplement de prédire si un objet était un randonneur, nous voudrions idéalement un nombre égal d’objets randonneur et non-randonneur :

Étiquette	Randonneur	Non randonneur
Count	1100	1100

Pourquoi le déséquilibre des données est-il important ?

Les données sont déséquilibrées, car les modèles peuvent apprendre à imiter ces déséquilibres lorsqu’ils ne sont pas souhaitables. Par exemple, imaginons que nous avons formé un modèle de régression logistique pour identifier les objets comme randonneur ou non-randonneur. Si les données d’entraînement étaient fortement dominées par des étiquettes « randonneur », l’entraînement aurait pour effet de biaiser le modèle qui retournerait presque toujours des étiquettes « randonneur ». Dans le monde réel, cependant, nous pouvons constater que la plupart des choses que les drones voient sont des arbres. Le modèle biaisé nommerait probablement un grand nombre de ces arbres comme randonneurs.

Ce phénomène a lieu car les fonctions de coût, par défaut, déterminent si la réponse correcte a été donnée. Cela signifie que pour un jeu de données biaisé, le moyen le plus simple pour un modèle d’atteindre des performances optimales peut être d’ignorer pratiquement les fonctionnalités fournies et toujours, ou presque toujours, renvoyer la même réponse. Cela peut avoir des conséquences dévastatrices. Par exemple, imaginez que notre modèle randonneur/non-randonneur est entraîné sur des données où seul un échantillon sur 1 000 contient un randonneur. Un modèle qui a appris à retourner « non-randonneur » à chaque fois a une justesse de 99,9% ! Ces statistiques sont exceptionnelles, mais le modèle est inutile, car elle ne vous indiquera jamais si une personne se trouve sur la montagne, et nous ne saurons pas qu’il faut les secourir en cas d’avalanche.

Écart dans une matrice de confusion

Les matrices de confusion sont la clé de l’identification des écarts de données ou du modèle. Dans un scénario idéal, les données de test ont un nombre pair d’étiquettes, et les prédictions effectuées par le modèle sont également approximativement réparties entre les étiquettes. Pour 1 000 échantillons, un modèle qui est non biaisé, mais qui a souvent des réponses erronées, peut ressembler à ceci :

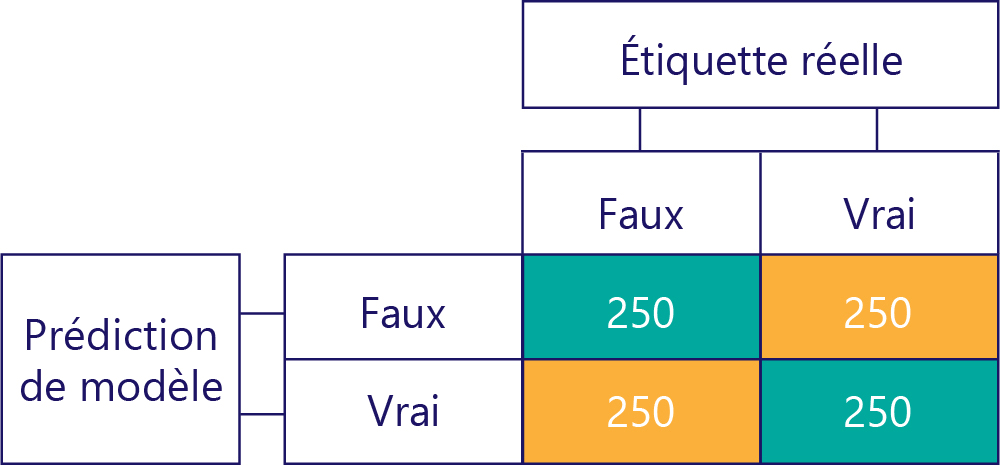
Nous pouvons dire que les données d’entrée sont non biaisées, car les sommes des lignes sont les mêmes (500 chacune), ce qui indique que la moitié des étiquettes a la valeur « True » et l’autre moitié la valeur « False ». De la même façon, nous pouvons voir que le modèle donne des réponses non biaisées, car il retourne la valeur True à 50 %.

En revanche, les données biaisées contiennent principalement un type d’étiquette, comme suit :

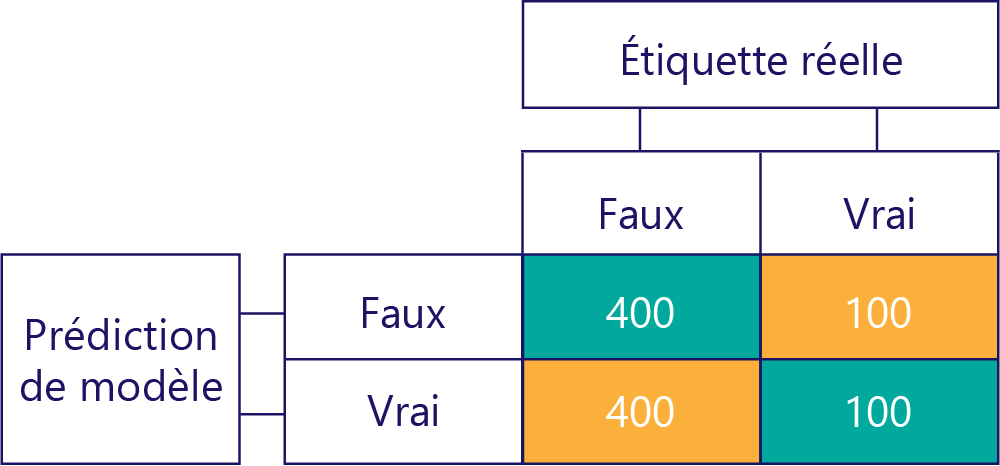
Un modèle biaisé produit essentiellement un type d’étiquette, comme suit :

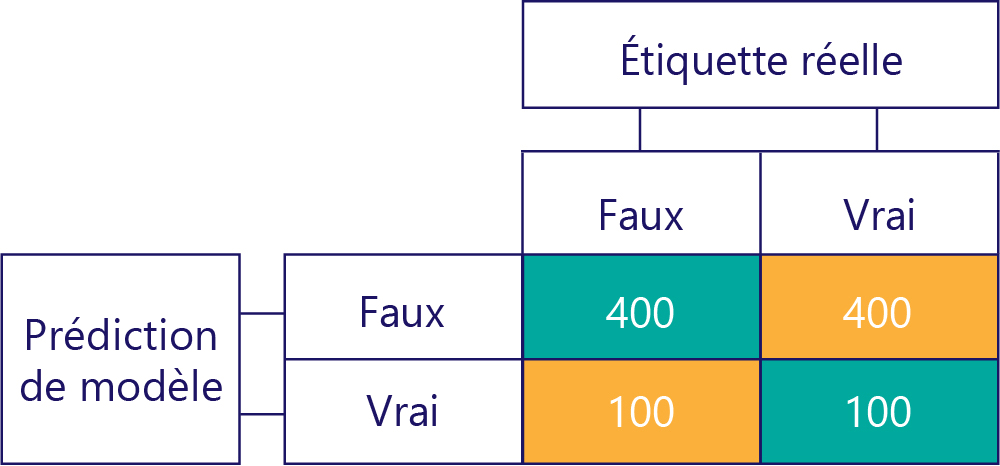
L’écart du modèle n’est pas exact

N’oubliez pas que l’écart n’est pas exact. Par exemple, certains des exemples précédents sont biaisés, tandis que d’autres ne le sont pas, mais ils montrent tous un modèle qui obtient la réponse correcte 50 % du temps. En guise d’exemple plus extrême, le tableau ci-dessous montre un modèle non biaisé qui est inexact :

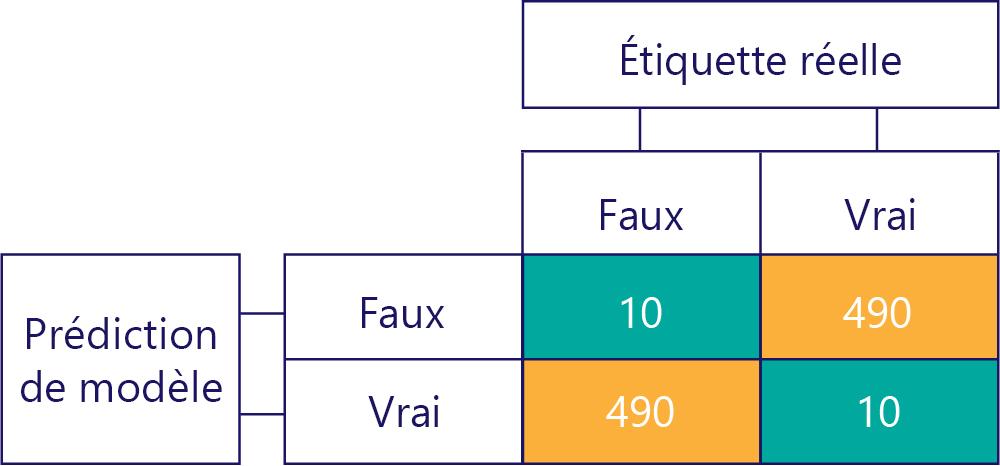
Notez que le nombre de lignes et de colonnes est 500, ce qui indique que les données sont équilibrées et que le modèle n’est pas biaisé. Toutefois, ce modèle obtient presque que des réponses incorrectes.

Bien entendu, notre objectif est de faire en sorte que les modèles soient exacts et non biaisés, par exemple :

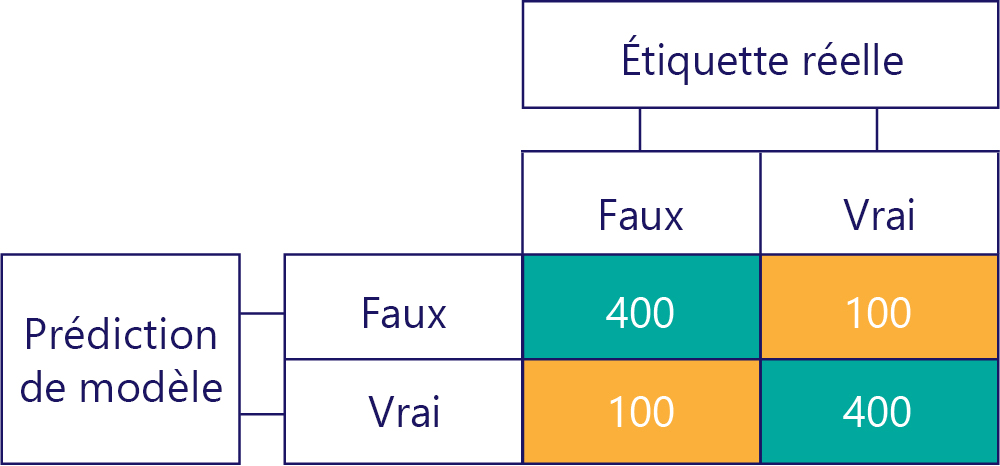
Nous devons nous assurer que nos modèles exacts ne sont pas biaisés, simplement parce que les données sont les suivantes :

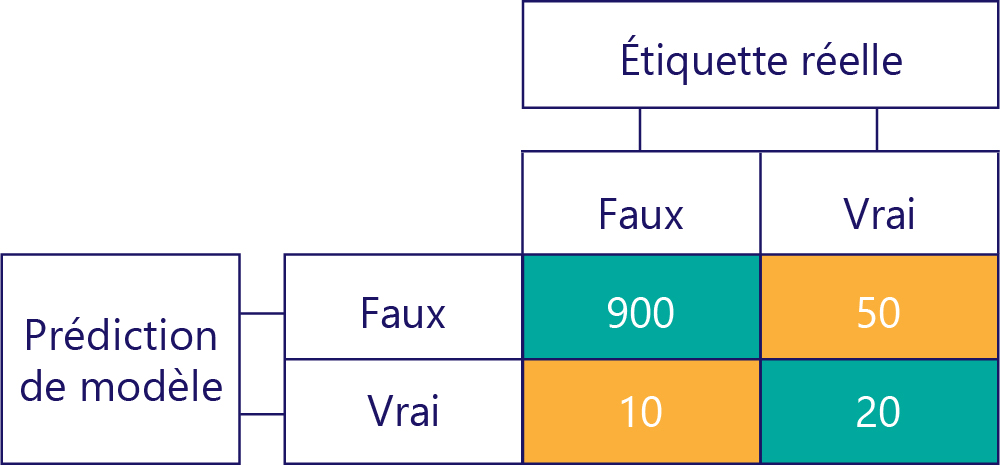
Dans cet exemple, les étiquettes réelles sont généralement fausses (colonne de gauche, avec un déséquilibre de données) et le modèle renvoie souvent False (ligne du haut, affichage du décalage du modèle). Ce modèle ne donne pas les réponses « True » correctement.

Éviter les conséquences des données déséquilibrées

Voici quelques-unes des manières les plus simples d’éviter les conséquences des données déséquilibrées :

• Évitez-les grâce à une meilleure sélection des données.
• « Rééchantillonnez » vos données afin qu’elles contiennent des doublons de la classe d’étiquettes minoritaires.
• Apportez des modifications à la fonction coût afin d’établir la priorité des étiquettes moins courantes. Par exemple, si une réponse incorrecte est donnée pour Arbre, la fonction de coût peut retourner 1, tandis que si la réponse incorrecte est faite pour Randonneur, elle peut retourner 10.

Nous allons explorer ces méthodes dans l’exercice suivant.