Matrices de confusion
Les données peuvent être considérées comme continues, en catégories ou ordinales (en catégories mais avec un certain ordre). Les matrices de confusion sont un moyen d’évaluer les performances d’un modèle en catégories. Pour connaître le contexte de ces opérations, nous allons tout d’abord actualiser nos connaissances sur les données continues. Nous pouvons ainsi voir comment les matrices de confusion sont simplement une extension des histogrammes que nous connaissons déjà.
Distributions de données en continu
Lorsque nous souhaitons comprendre les données en continu, la première étape est souvent de voir comment elles sont distribuées. Considérons l’histogramme suivant :
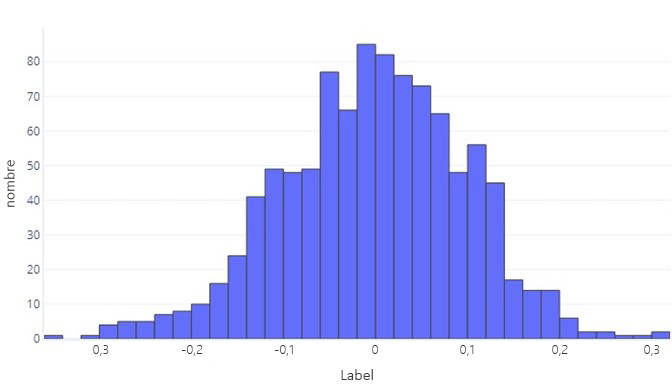
Nous pouvons voir que l’étiquette est, en moyenne, environ zéro, et que la plupart des points de contrôle sont compris entre -1 et 1. Il apparaît comme symétrique : il y a approximativement autant de nombres au-dessous qu’au-dessus de la moyenne. Si nous le souhaitions, nous pourrions utiliser une table plutôt qu’un histogramme, mais cela peut être moins pratique.
Distributions de données en catégorie
À certains égards, les données en catégorie ne sont pas si différentes des données en continu. Nous pouvons toujours produire des histogrammes pour évaluer la façon dont les valeurs sont généralement affichées pour chaque étiquette. Par exemple, une étiquette binaire (True/False) peut apparaître avec cette fréquence :
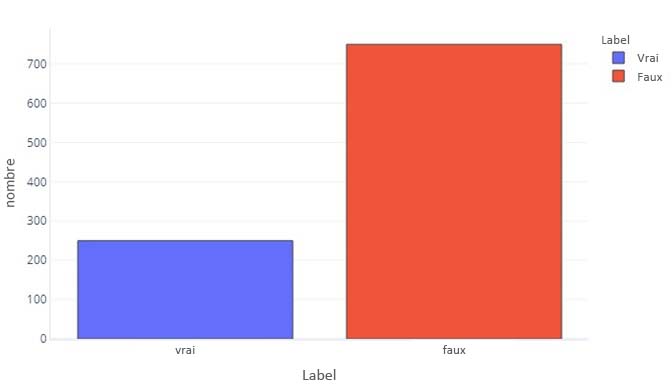
Cela nous indique qu’il existe 750 échantillons avec une étiquette « False », et 250 avec une étiquette « True ».
Une étiquette pour trois catégories est similaire :
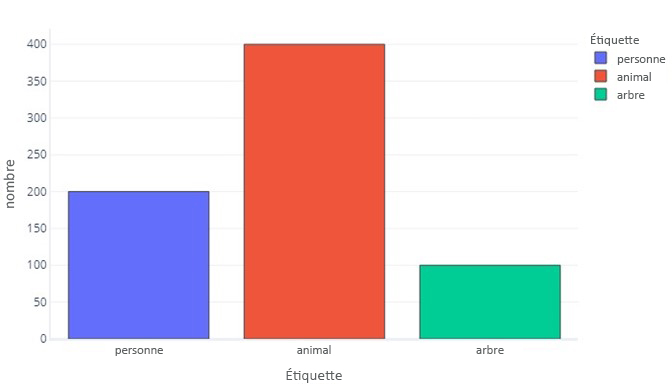
Ceci nous indique qu’il existe 200 échantillons qui sont « personne », 400 qui sont « animal » et 100 qui sont « arbre ».
Les étiquettes en catégories étant plus simples, nous pouvons souvent les afficher sous forme de tables simples. Les deux graphes précédents auraient l’apparence suivante :
| Étiquette | False | True |
|---|---|---|
| Count | 750 | 250 |
Et :
| Étiquette | Personne | Animal | Arborescence |
|---|---|---|---|
| Count | 200 | 400 | 100 |
Examen des prédictions
Nous pouvons examiner les prédictions que le modèle effectue de la même façon que nous observons les étiquettes réelles dans nos données. Par exemple, nous pouvons voir que dans notre jeu de test, notre modèle a prédit 700 « False » et 300 fois « True ».
| Prédiction de modèle | Count |
|---|---|
| False | 700 |
| True | 300 |
Cela fournit des informations concrètes sur les prédictions faites par notre modèle, mais ne nous dit pas quelles sont les prédictions correctes. Bien que nous puissions utiliser une fonction de coût pour comprendre la fréquence à laquelle les réponses correctes sont fournies, cette fonction ne nous indiquera pas quels types d’erreurs sont commises. Par exemple, le modèle peut deviner correctement toutes les valeurs « True », mais qu’il devine aussi « True » quand il aurait dû deviner « False ».
La matrice de confusion
Pour comprendre les performances du modèle, il est essentiel de combiner la table pour la prédiction de modèle avec la table pour les étiquettes de données réelles :
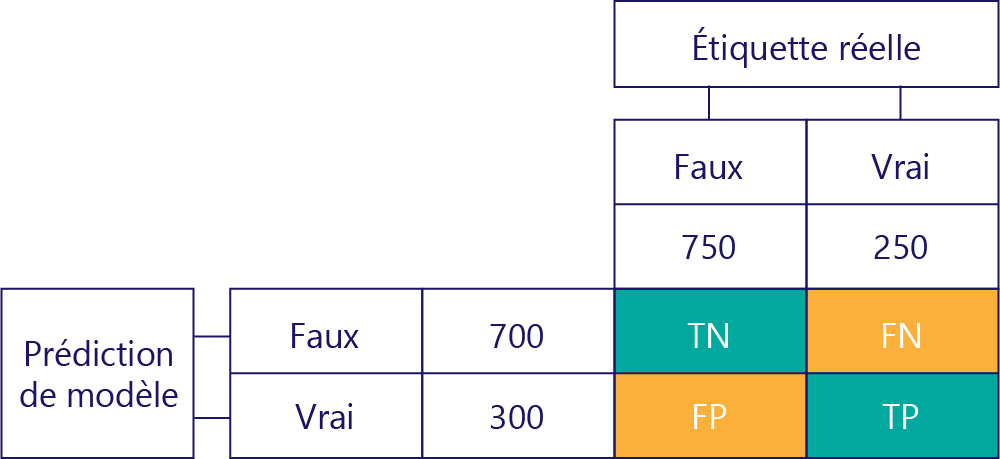
Le carré que nous n’avons pas rempli est appelé matrice de confusion.
Chaque cellule de la matrice de confusion nous dit quelque chose sur les performances du modèle. Il s’agit de vrais négatifs (TN), de faux négatifs (FN), de faux positifs (FP) et de vrais positifs (TP).
Nous allons les expliquer un par un, en remplaçant ces acronymes par des valeurs réelles. Les carrés bleu-vert signifient que le modèle a effectué une prédiction correcte, et les carrés orange signifient que le modèle a fait une prédiction incorrecte.
Vrais négatifs (TN)
La valeur en haut à gauche répertorie le nombre de fois où le modèle a prédit la valeur False et l’étiquette réelle a également la valeur False. En d’autres termes, cela indique le nombre de fois que le modèle a prédit correctement la valeur False. Supposons, pour notre exemple, que cela s’est produit 500 fois :

Faux négatifs (FN)
La valeur supérieure droite indique combien de fois le modèle a prédit la valeur False, mais l’étiquette réelle a la valeur True. Nous savons maintenant que la valeur est égale à 200. Comment faire ? Étant donné que le modèle a prédit la valeur False 700 fois, dont 500 fois correctement. Ainsi, il a prédit la valeur False 200 fois alors qu’il n’aurait pas dû.
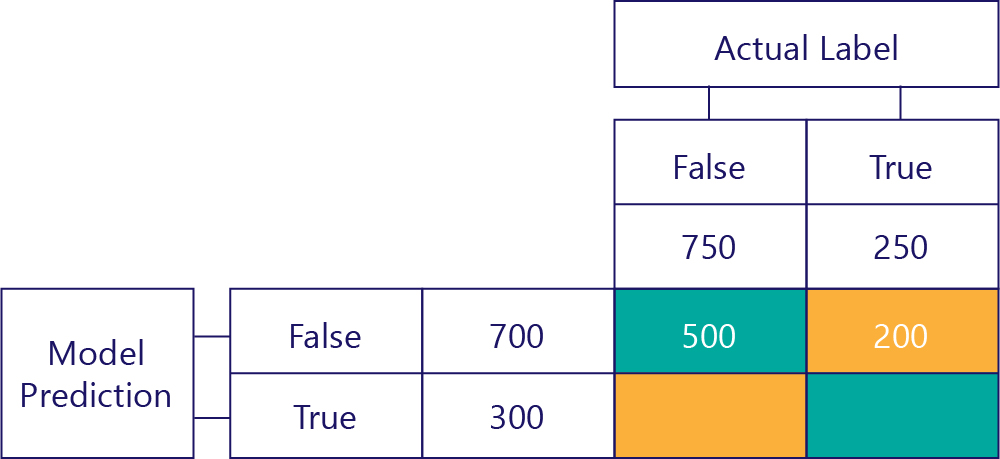
Faux positif (FP)
La valeur inférieure gauche contient des faux positifs. Cela nous indique combien de fois le modèle a prédit la valeur True, mais l’étiquette réelle a la valeur False. Nous savons maintenant qu’il s’agit de 250, car il y avait 750 fois où la réponse correcte était False. 500 de ces fois s’affichent dans la cellule supérieure gauche (TN) :
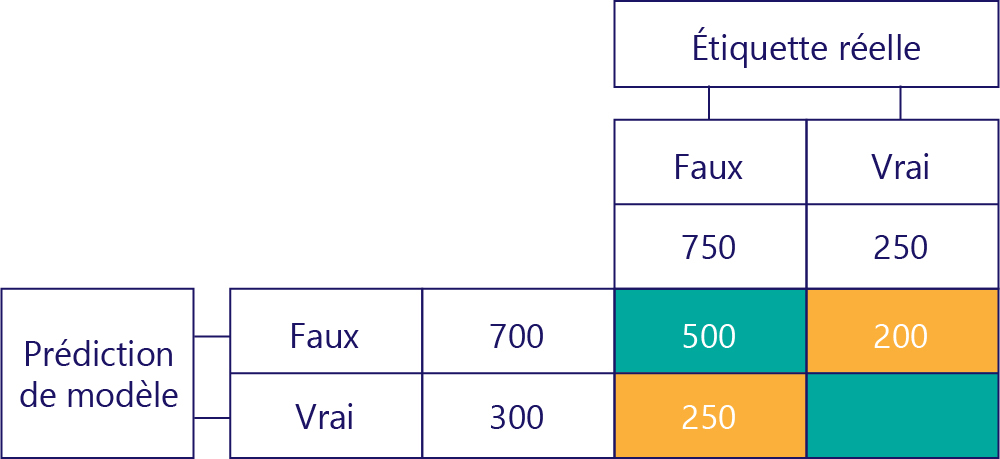
Vrais positifs (TP)
Enfin, nous avons les vrais positifs. Il s’agit du nombre de fois que le modèle prédit correctement la valeur True. Nous savons qu’il s’agit de la valeur 50 pour deux raisons. Tout d’abord, le modèle a prédit la valeur True 300 fois, mais 250 fois de fa_on incorrecte (cellule en bas à gauche). Deuxièmement, il y avait 250 fois la réponse True, mais le modèle a prédit 200 fois la valeur False.
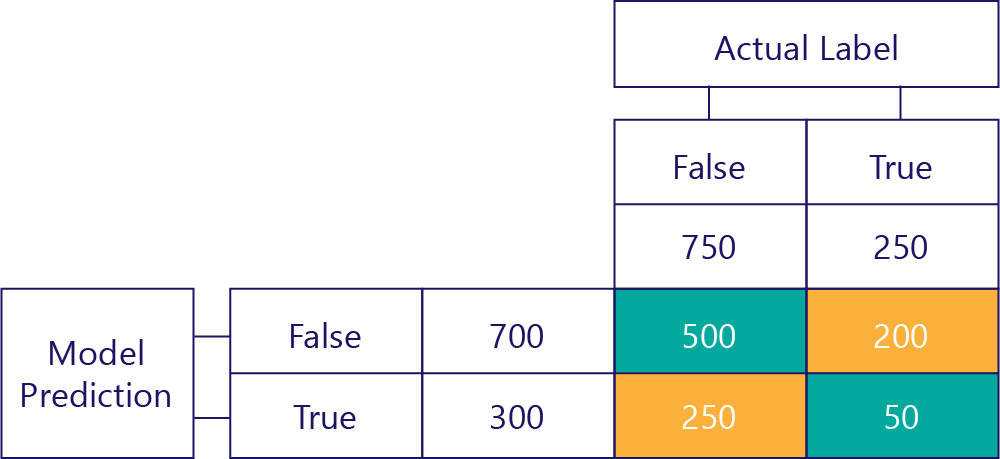
La matrice finale
Nous simplifions généralement légèrement notre matrice de confusion, comme suit :
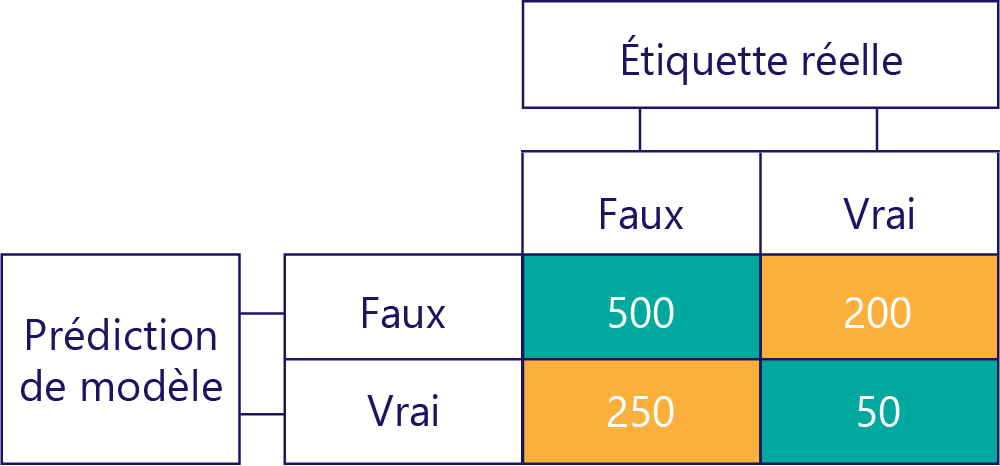
Nous avons coloré les cellules ici pour mettre en évidence le moment où le modèle a effectué des prédictions correctes. À partir de là, nous connaissons non seulement la fréquence à laquelle le modèle a fait certains types de prédictions, mais aussi la fréquence à laquelle ces prédictions étaient correctes ou incorrectes.
Les matrices de confusion peuvent également être construites lorsqu’il y a plus d’étiquettes. Par exemple, pour notre exemple de personne/animal/arbre, nous pouvons obtenir une matrice comme celle-ci :
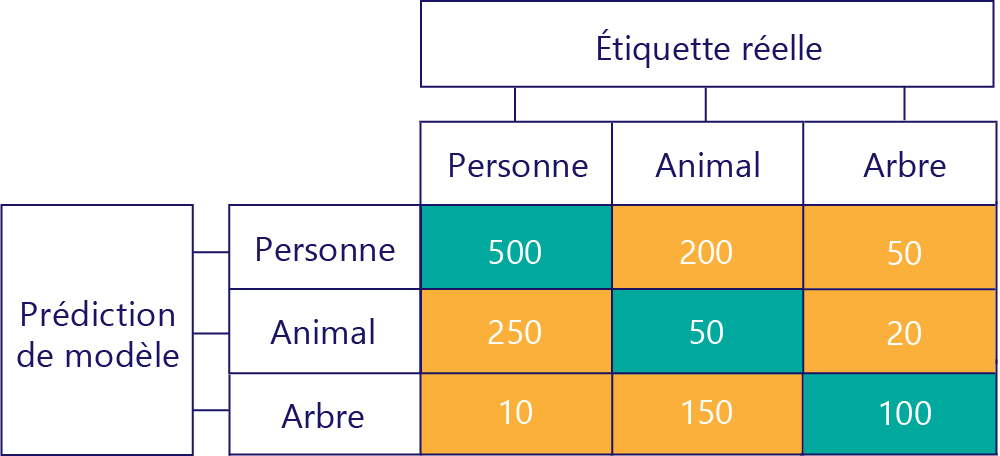
Lorsqu’il existe trois catégories, les mesures comme les vrais positifs ne s’appliquent plus, mais nous pouvons toujours voir exactement la fréquence à laquelle le modèle a commis certains genres d’erreurs. Par exemple, nous pouvons voir que le modèle a prédit « personne » 200 fois, alors que le résultat réel correct était « animal ».