Vecteurs 1 parmi n
Jusqu’à présent, nous avons abordé l’encodage des données continues (nombres à virgule flottante), des données ordinales (généralement des entiers) et des données catégorielles binaires (survivant/décédé, homme/femme etc.).
Nous allons maintenant apprendre à encoder des données et explorer les ressources de données catégorielles qui ont plus de deux classes. Nous allons également explorer les effets potentiellement nocifs de nos décisions d’amélioration du modèle sur le niveau de performance du modèle.
Les données catégorielles ne sont pas numériques
Les données catégorielles ne fonctionnent pas avec les nombres de la même façon que les autres types de données. Avec des données ordinales ou continues (numériques), les valeurs supérieures impliquent une augmentation de quantité. Par exemple, le prix d’un billet Titanic de 30 £ représente une somme plus élevée que le prix d’un billet de 12 £.
En revanche, les données catégorielles n’ont pas d’ordre logique. Nous aurons des problèmes si nous essayons d’encoder, sous forme de nombres, des caractéristiques catégorielles qui ont plus de deux classes.
Par exemple, le Port d’embarquement a trois valeurs : C (Cherbourg), Q (Queenstown) et S (Southampton). Nous ne pouvons pas remplacer ces symboles par des nombres. Si nous le faisons, cela impliquerait que l’un de ces ports est inférieur aux autres ports, tandis qu’un autre est supérieur aux autres ports. Ce remplacement n’a aucun sens.
Pour illustrer ce problème, prenons des précautions et modélisons la relation entre le Port d’embarquement et la Classe de billet, en traitant le Port d’embarquement comme un nombre. Tout d’abord, nous définissons C < S < Q :
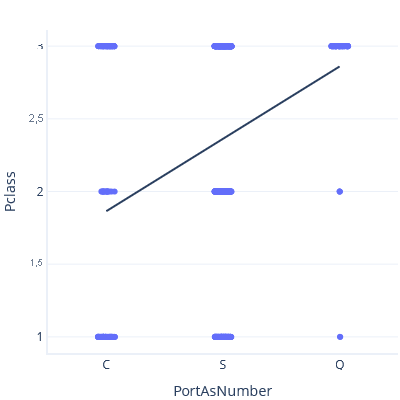
Dans ce tracé, la ligne prédit une Classe d’environ 3 pour le port Q.
À présent, si nous définissons S < C < Q, nous obtenons une courbe de tendance et une prédiction différentes :
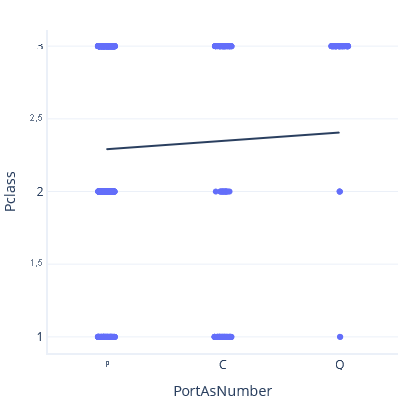
Aucune de ces courbes de tendance n’est correcte. Il est inutile de traiter les catégories comme des fonctionnalités continues. Donc, comment utiliser des catégories ?
Encodage à chaud
L’encodage one-hot peut encoder des données catégorielles d’une manière qui évite ce problème. Chaque catégorie disponible a sa propre colonne et une ligne donnée ne contient qu’une seule valeur 1 dans la catégorie à laquelle elle appartient.
Par exemple, nous pouvons encoder la valeur de port en trois colonnes : une pour Cherbourg, une pour Queenstown et une pour Southampton (l’ordre exact ici n’a aucune pertinence). Une personne ayant embarqué à Cherbourg aurait un 1 dans la colonne Port_Cherbourg, comme suit :
| Port_Cherbourg | Port_Queenstown | Port_Southampton |
|---|---|---|
| 1 | 0 | 0 |
Une personne ayant embarqué à Queenstown aurait un 1 dans la deuxième colonne :
| Port_Cherbourg | Port_Queenstown | Port_Southampton |
|---|---|---|
| 0 | 1 | 0 |
Une personne ayant embarqué à Southampton aurait un 1 dans la troisième colonne
| Port_Cherbourg | Port_Queenstown | Port_Southampton |
|---|---|---|
| 0 | 0 | 1 |
Encodage 1 parmi n, nettoyage des données et puissance statistique
Avant d’utiliser l’encodage one-hot, il est important de comprendre que son utilisation peut avoir un impact positif ou négatif sur le niveau de performance réel d’un modèle.
Qu’est-ce que la puissance statistique ?
La puissance statistique fait référence à la capacité d’un modèle à identifier de manière fiable les relations réelles entre les caractéristiques et les étiquettes. Par exemple, un modèle puissant peut signaler une relation entre le prix du billet et le taux de survie avec un degré élevé de certitude. En revanche, un modèle avec une faible puissance statistique peut signaler une relation avec un faible degré de certitude ou peut même ne pas trouver cette relation du tout.
Nous allons ici éviter les calculs, mais n’oubliez pas que les choix que nous faisons peuvent influencer la puissance de nos modèles.
La suppression de données réduit la puissance statistique
Nous avons mentionné plusieurs fois que le nettoyage des données implique, en partie, la suppression d’exemples de données incomplets. Malheureusement, le nettoyage des données peut réduire la puissance statistique. Par exemple, supposons que nous voulions prédire la survie lors du voyage sur le Titanic en fonction des données suivantes :
| Prix du billet | Survie |
|---|---|
| 4 £ | 0 |
| 8 £ | 0 |
| 10 £ | 1 |
| 25 £ | 1 |
Nous pourrions deviner qu’une personne ayant un billet d’une valeur de 15 £ survivrait, car les personnes ayant des billets d’une valeur supérieure ou égale à 10 £ ont toutes survécu. Si nous avions moins de données, cependant, cette estimation deviendrait plus difficile :
| Prix du billet | Survie |
|---|---|
| 4 £ | 0 |
| 8 £ | 0 |
| 25 £ | 1 |
Les colonnes sans valeur réduisent la puissance statistique
Les caractéristiques à faible valeur peuvent également endommager la puissance statistique, en particulier lorsque le nombre de caractéristiques (ou colonnes) commence à s’approcher du nombre d’échantillons (ou lignes).
Par exemple, disons que nous voulons être en mesure de prédire la survie en fonction des données suivantes :
| Prix du billet | Survie |
|---|---|
| 4 £ | 0 |
| 4 £ | 0 |
| 25 £ | 1 |
| 25 £ | 1 |
Nous pourrions prévoir, en toute confiance, qu’une personne avec un billet de Cabine A survivrait, car toutes les personnes ayant des billets de 25 £ ont survécu.
Toutefois, nous avons maintenant une autre caractéristique (Cabine) :
| Prix du billet | Cabin | Survie |
|---|---|---|
| 4 £ | A | 0 |
| 4 £ | A | 0 |
| 25 £ | B | 1 |
| 25 £ | B | 1 |
La caractéristique Cabine ne fournit pas d’informations utiles, car elle correspond simplement au prix du billet. Il n’est pas certain qu’une personne avec un billet de 25 £ pour la cabine A survivrait. Périssent-ils comme d’autres occupants de la cabine A ou survivent-ils comme ceux munis de billets de 25 £ ?
L’encodage 1 parmi n peut réduire la puissance statistique
L’encodage à chaud réduit davantage la puissance statistique que les données continues ou ordinales, car il nécessite plusieurs colonnes (une pour chaque valeur catégorielle possible). Par exemple, en procédant à l’encodage 1 parmi n du port d’embarquement, nous ajoutons trois entrées de modèle (C, S et Q).
Une variable catégorielle devient utile si le nombre de catégories est sensiblement inférieur au nombre d’échantillons (lignes de jeu de données). Une variable de catégorie devient également utile si elle fournit des informations qui ne sont pas déjà disponibles pour le modèle dans d’autres entrées.
Par exemple, nous avons vu que la probabilité de survie était différente pour les personnes ayant embarqué à des ports différents. Cette variation reflète vraisemblablement que la plupart des personnes au port de Queenstown avaient des billets de troisième classe. Par conséquent, l’embarquement réduit probablement légèrement la puissance statistique, sans ajouter d’informations pertinentes à notre modèle.
En revanche, la cabine est susceptible d’avoir une influence forte sur la survie. En effet, les cabines inférieures du navire auraient été submergées avant les cabines plus proches du pont du navire. Cela dit, le jeu de données Titanic contient 147 cabines différentes. Cela réduit la puissance statistique de notre modèle si nous les incluons. Il est possible que nous devions faire une expérience en incluant ou excluant les données Cabine dans notre modèle pour voir si ces données peuvent nous aider.
Dans notre prochain exercice, nous allons créer notre modèle de prédiction de survie lors du voyage sur le Titanic en expérimentant l’encodage one-hot.