Classification multiclasse
La classification multiclasse est utilisée pour prédire les possibles classes d’appartenance d’une observation. En tant que technique de Machine Learning supervisée, elle suit le même processus itératif d’apprentissage, de validation et d’évaluation que la régression et la classification binaire dans lesquelles un sous-ensemble des données d’entraînement est retenu pour valider le modèle entraîné.
Exemple – classification multiclasse
Les algorithmes de classification multiclasse servent à calculer des valeurs de probabilité pour plusieurs étiquettes de classe, ce qui permet à un modèle de prédire la classe la plus probable pour une observation donnée.
Examinons un exemple dans lequel nous avons quelques observations de manchots dans lequel la longueur de la nageoire (x) de chaque pingouin est enregistrée. Pour chaque observation, les données comprennent l’espèce de pingouin (y) qui est encodée comme suit :
- 0 : Adelie
- 1 : Manchot papou
- 2 : Manchot à jugulaire
Remarque
Comme dans les exemples précédents de ce module, un scénario réel contient plusieurs valeurs (x) de caractéristiques. Nous allons utiliser une seule fonctionnalité pour simplifier les choses.
 |
 |
|---|---|
| Longueur de la nageoire (x) | Espèces (y) |
| 167 | 0 |
| 172 | 0 |
| 225 | 2 |
| 197 | 1 |
| 189 | 1 |
| 232 | 2 |
| 158 | 0 |
Entraînement d’un modèle de classification multiclasse
Pour entraîner un modèle de classification multiclasse, nous devons nous servir d’un algorithme pour ajuster les données d’apprentissage à une fonction qui calcule une valeur de probabilité pour chaque classe possible. Pour y parvenir, vous pouvez utiliser deux types d’algorithmes :
- Algorithmes One-vs-Rest (OvR)
- Algorithmes multinomiaux
Algorithmes One-vs-Rest (OvR)
Les algorithmes One-vs-Rest entraînent une fonction de classification binaire pour chaque classe, chacun évaluant la probabilité que l’observation soit un exemple de classe cible. Chaque fonction calcule la probabilité que l’observation appartienne à une classe spécifique par rapport à toute autre classe. Pour notre modèle de classification des espèces de manchots, l’algorithme crée essentiellement trois fonctions de classification binaire :
- f0(x) = P(y=0 | x)
- f1(x) = P(y=1 | x)
- f2(x) = P(y=2 | x)
Chaque algorithme produit une fonction sigmoïde qui calcule une valeur de probabilité située entre 0,0 et 1,0. Un modèle entraîné avec ce type d’algorithme prédit la classe pour la fonction qui produit la sortie de probabilité la plus élevée.
Algorithmes multinomiaux
Une autre approche consiste à utiliser un algorithme multinomial qui crée une fonction unique, retournant une sortie à valeurs multiples. La sortie est un vecteur (tableau de valeurs) qui contient la distribution de probabilité pour toutes les classes possibles (avec un score de probabilité pour chaque classe qui, lorsqu’il est totalisé, ajoute jusqu’à 1,0) :
f(x) =[P(y=0|x), P(y=1|x), P(y=2|x)]
Un exemple de ce type de fonction est une fonction softmax qui peut produire une sortie proche de l’exemple suivant :
[0,2, 0,3, 0,5]
Les éléments du vecteur représentent les probabilités d’obtenir respectivement les classes 0, 1 et 2. Dans ce cas, la classe avec la probabilité la plus élevée est 2.
Quel que soit le type d’algorithme utilisé, le modèle prend la fonction résultante pour déterminer la classe la plus probable pour un ensemble donné de caractéristiques (x) et prédit en conséquence l’étiquette de classe (y).
Évaluation d’un modèle de classification multiclasse
Vous pouvez évaluer un classificateur multiclasse en calculant les métriques de classification binaire de chaque classe individuelle. Vous pouvez également calculer des métriques agrégées qui prennent en compte toutes les classes.
Supposons que nous ayons validé notre classificateur multiclasse et obtenu les résultats suivants :
| Longueur de la nageoire (x) | Espèces réelles (y) | Espèces prédites (ŷ) |
|---|---|---|
| 165 | 0 | 0 |
| 171 | 0 | 0 |
| 205 | 2 | 1 |
| 195 | 1 | 1 |
| 183 | 1 | 1 |
| 221 | 2 | 2 |
| 214 | 2 | 2 |
La matrice de confusion pour un classificateur de classeur multiclassement est semblable à celle d’un classificateur binaire, sauf qu’elle montre le nombre de prédictions pour chaque combinaison d’étiquettes de classe prédites (ŷ) et réelles (y) :
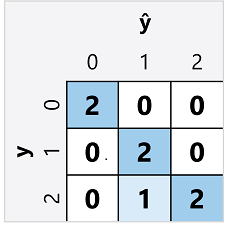
À partir de cette matrice de confusion, nous pouvons déterminer les métriques de chaque classe individuelle comme suit :
| Classe | TP | TN | FP | FN | Exactitude | Rappel | Precision | Score F1 |
|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 5 | 0 | 0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 1 | 2 | 4 | 1 | 0 | 0,86 | 1.0 | 0.67 | 0,8 |
| 2 | 2 | 4 | 0 | 1 | 0,86 | 0.67 | 1.0 | 0,8 |
Pour calculer les métriques globales d’exactitude, de rappel et de précision, vous utilisez l’ensemble des métriques TP, TN, FP et FN :
- Exactitude globale = (13+6)÷(13+6+1+1) = 0,90
- Rappel global = 6÷(6+1) = 0,86
- Précision globale = 6÷(6+1) = 0,86
Le score F1 global est calculé en utilisant des métriques globales de rappel et de précision :
- Score F1 global = (2x0,86x0,86)÷(0,86+0,86) = 0,86