Exercice - Effectuer une régression linéaire avec Numpy
Les nuages de points offrent un moyen pratique de visualiser les données, mais supposez que vous souhaitez superposer le nuage de points avec une courbe de tendance montrant comment les données évoluent au fil du temps. La régression linéaire est l’un des moyens de calculer ces courbes de tendance. Dans cet exercice, vous allez utiliser NumPy pour effectuer une régression linéaire et Matplotlib pour tracer une courbe de tendance à partir des données.
Placez le curseur dans la cellule vide en bas du notebook. Remplacez le type de cellule par Markdown et entrez « Effectuer une régression linéaire » comme texte.
Ajoutez une cellule Code et ajoutez-la dans le code suivant. Prenez un moment pour lire les commentaires (les lignes qui commencent par le signe #) pour comprendre ce que fait le code.
# Creates a linear regression from the data points m,b = np.polyfit(yearsBase, meanBase, 1) # This is a simple y = mx + b line function def f(x): return m*x + b # This generates the same scatter plot as before, but adds a line plot using the function above plt.scatter(yearsBase, meanBase) plt.plot(yearsBase, f(yearsBase)) plt.title('scatter plot of mean temp difference vs year') plt.xlabel('years', fontsize=12) plt.ylabel('mean temp difference', fontsize=12) plt.show() # Prints text to the screen showing the computed values of m and b print(' y = {0} * x + {1}'.format(m, b)) plt.show()Maintenant, exécutez la cellule pour afficher un nuage de points avec une ligne de régression.
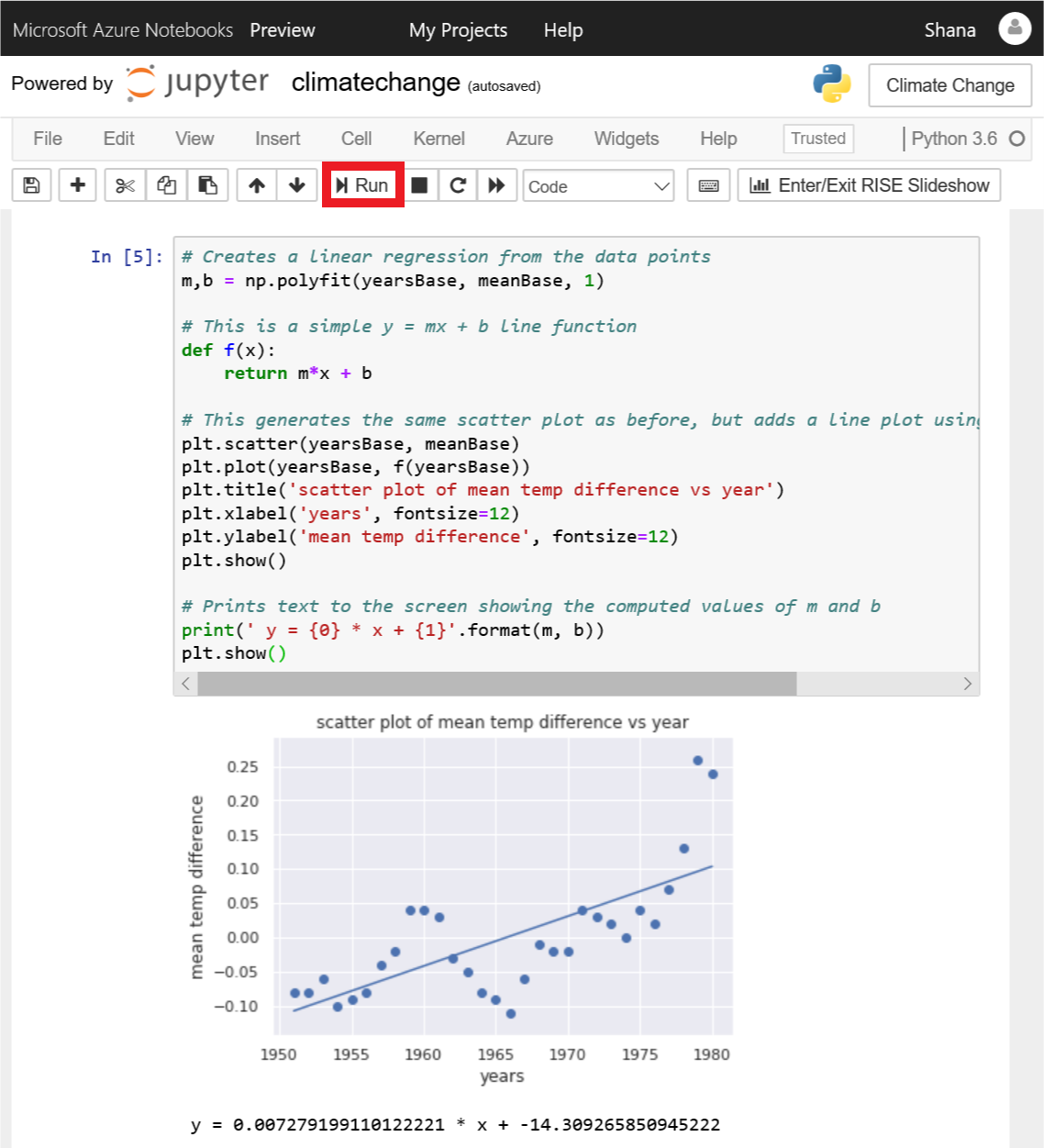
Nuage de points avec ligne de régression
Dans la ligne de régression, vous pouvez voir que la différence entre les températures moyennes sur 30 ans et les températures moyennes sur 5 ans augmente au fil du temps. L’essentiel du travail de calcul nécessaire pour générer la ligne de régression a été effectué par la fonction polyfit de NumPy, qui a calculé les valeurs de m et b dans l’équation y = mx + b.