Polylignes et équations paramétriques
Utilisez SkiaSharp pour afficher n’importe quelle ligne que vous pouvez définir avec des équations paramétriques
Dans la section Courbes et chemins skiaSharp de ce guide, vous verrez les différentes méthodes qui SKPath définissent pour afficher certains types de courbes. Toutefois, il est parfois nécessaire de dessiner un type de courbe qui n’est pas directement pris en charge par SKPath. Dans ce cas, vous pouvez utiliser une polyligne (collection de lignes connectées) pour dessiner n’importe quelle courbe que vous pouvez définir mathématiquement. Si vous faites les lignes assez petites et assez nombreuses, le résultat ressemblera à une courbe. Cette spirale est en fait 3 600 petites lignes :

En règle générale, il est préférable de définir une courbe en termes de paire d’équations paramétriques. Il s’agit d’équations pour les coordonnées X et Y qui dépendent d’une troisième variable, parfois appelée t pour le temps. Par exemple, les équations paramétriques suivantes définissent un cercle avec un rayon de 1 centré au point (0, 0) pour t de 0 à 1 :
x = cos(2πt)
y = sin(2πt)
Si vous souhaitez un rayon supérieur à 1, vous pouvez simplement multiplier les valeurs de sinus et de cosinus par ce rayon, et si vous devez déplacer le centre vers un autre emplacement, ajoutez ces valeurs :
x = xCenter + radius·cos(2πt)
y = yCenter + radius·sin(2πt)
Pour un ellipse avec les axes parallèles à l’horizontale et verticale, deux rayons sont impliqués :
x = xCenter + xRadius·cos(2πt)
y = yCenter + yRadius·sin(2πt)
Vous pouvez ensuite placer le code SkiaSharp équivalent dans une boucle qui calcule les différents points et les ajoute à un chemin d’accès. Le code SkiaSharp suivant crée un SKPath objet pour un ellipse qui remplit la surface d’affichage. La boucle passe directement à 360 degrés. Le centre est la moitié de la largeur et de la hauteur de la surface d’affichage, et ainsi sont les deux rayons :
SKPath path = new SKPath();
for (float angle = 0; angle < 360; angle += 1)
{
double radians = Math.PI * angle / 180;
float x = info.Width / 2 + (info.Width / 2) * (float)Math.Cos(radians);
float y = info.Height / 2 + (info.Height / 2) * (float)Math.Sin(radians);
if (angle == 0)
{
path.MoveTo(x, y);
}
else
{
path.LineTo(x, y);
}
}
path.Close();
Cela entraîne une ellipse définie par 360 petites lignes. Lorsqu’il est rendu, il apparaît lisse.
Bien sûr, vous n’avez pas besoin de créer un ellipse à l’aide d’une polyline, car SKPath inclut une AddOval méthode qui le fait pour vous. Mais vous souhaiterez peut-être dessiner un objet visuel qui n’est pas fourni par SKPath.
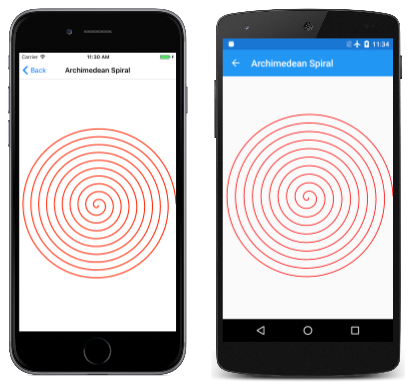
La page Spirale Archimedean a du code similaire au code ellipse, mais avec une différence cruciale. Il effectue une boucle autour des 360 degrés du cercle 10 fois, en ajustant en continu le rayon :
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
float radius = Math.Min(center.X, center.Y);
using (SKPath path = new SKPath())
{
for (float angle = 0; angle < 3600; angle += 1)
{
float scaledRadius = radius * angle / 3600;
double radians = Math.PI * angle / 180;
float x = center.X + scaledRadius * (float)Math.Cos(radians);
float y = center.Y + scaledRadius * (float)Math.Sin(radians);
SKPoint point = new SKPoint(x, y);
if (angle == 0)
{
path.MoveTo(point);
}
else
{
path.LineTo(point);
}
}
SKPaint paint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Red,
StrokeWidth = 5
};
canvas.DrawPath(path, paint);
}
}
Le résultat est également appelé spirale arithmétique , car le décalage entre chaque boucle est constant :
Notez que le fichier SKPath est créé dans un using bloc. Cela SKPath consomme plus de mémoire que les SKPath objets des programmes précédents, ce qui suggère qu’un using bloc est plus approprié pour supprimer les ressources non managées.