Trois façons de dessiner un arc

Découvrez comment utiliser SkiaSharp pour définir des arcs de trois façons différentes

Un arc est une courbe sur la circonférence d’un ellipse, comme les parties arrondies de ce signe infini :

Malgré la simplicité de cette définition, il n’existe aucun moyen de définir une fonction de dessin à arc qui répond à tous les besoins, et par conséquent, aucun consensus entre les systèmes graphiques de la meilleure façon de dessiner un arc. Pour cette raison, la SKPath classe ne se limite pas à une seule approche.

SKPath définit une AddArc méthode, cinq méthodes différentes ArcTo et deux méthodes relatives RArcTo . Ces méthodes appartiennent à trois catégories, représentant trois approches très différentes pour spécifier un arc. Celui que vous utilisez dépend des informations disponibles pour définir l’arc, et de la façon dont cet arc s’adapte aux autres graphiques que vous dessinez.

Arc d’angle

L’approche de l’arc d’angle pour dessiner des arcs nécessite que vous spécifiiez un rectangle qui limite un ellipse. L’arc sur la circonférence de cet ellipse est indiqué par des angles du centre de l’ellipse qui indiquent le début de l’arc et sa longueur. Deux méthodes différentes dessinent des arcs d’angle. Il s’agit de la AddArc méthode et de la ArcTo méthode :

public void AddArc (SKRect oval, Single startAngle, Single sweepAngle)

public void ArcTo (SKRect oval, Single startAngle, Single sweepAngle, Boolean forceMoveTo)

Ces méthodes sont identiques aux méthodes Android AddArc et [ArcTo]xref :Android.Graphics.Path.ArcTo*). La méthode iOS AddArc est similaire, mais elle est limitée aux arcs sur la circonférence d’un cercle plutôt que généralisée à un ellipse.

Les deux méthodes commencent par une SKRect valeur qui définit à la fois l’emplacement et la taille d’un ellipse :

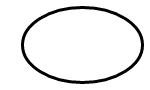
L’arc fait partie de la circonférence de cet ellipse.

L’argument startAngle est un angle au niveau des aiguilles d’une montre par rapport à une ligne horizontale dessinée du centre de l’ellipse à droite. L’argument sweepAngle est relatif au startAngle. Voici les startAngle sweepAngle valeurs de 60 degrés et 100 degrés, respectivement :

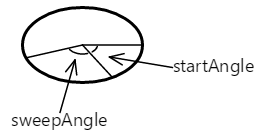
L’arc commence à l’angle de début. Sa longueur est régie par l’angle de balayage. L’arc est illustré ici en rouge :

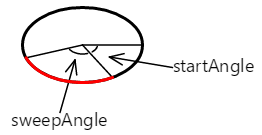
La courbe ajoutée au chemin d’accès avec la ou ArcTo la AddArc méthode est simplement cette partie de la circonférence de l’ellipse :

Les startAngle arguments sweepAngle ou les arguments peuvent être négatifs : l’arc est dans le sens des aiguilles d’une montre pour les valeurs positives et sweepAngle dans le sens inverse des aiguilles d’une montre pour les valeurs négatives.

Toutefois, AddArc ne définit pas de contour fermé. Si vous appelez LineTo après AddArc, une ligne est dessinée de la fin de l’arc au point de la LineTo méthode, et la même chose est vraie .ArcTo

AddArc démarre automatiquement un nouveau contour et est fonctionnellement équivalent à un appel avec ArcTo un argument final de true:

path.ArcTo (oval, startAngle, sweepAngle, true);

Ce dernier argument est appelé forceMoveTo, et il provoque efficacement un MoveTo appel au début de l’arc. Cela commence un nouveau contour. Ce n’est pas le cas avec un dernier argument de false:

path.ArcTo (oval, startAngle, sweepAngle, false);

Cette version de ArcTo dessine une ligne de la position actuelle au début de l’arc. Cela signifie que l’arc peut être quelque part au milieu d’un contour plus grand.

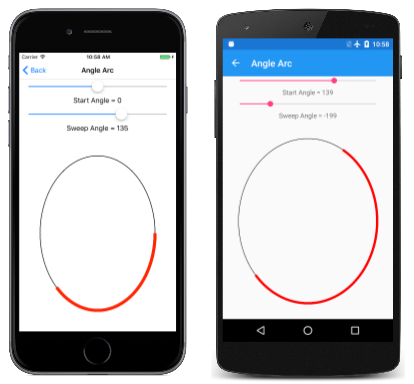
La page Angle Arc vous permet d’utiliser deux curseurs pour spécifier les angles de début et de balayage. Le fichier XAML instancie deux Slider éléments et un SKCanvasView. Le PaintCanvas gestionnaire dans le fichier AngleArcPage.xaml.cs dessine à la fois l’ovale et l’arc à l’aide de deux SKPaint objets définis en tant que champs :

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    SKRect rect = new SKRect(100, 100, info.Width - 100, info.Height - 100);
    float startAngle = (float)startAngleSlider.Value;
    float sweepAngle = (float)sweepAngleSlider.Value;

    canvas.DrawOval(rect, outlinePaint);

    using (SKPath path = new SKPath())
    {
        path.AddArc(rect, startAngle, sweepAngle);
        canvas.DrawPath(path, arcPaint);
    }
}

Comme vous pouvez le voir, l’angle de début et l’angle de balayage peuvent prendre des valeurs négatives :

Cette approche de la génération d’un arc est algorithmiquement la plus simple, et il est facile de dériver les équations paramétriques qui décrivent l’arc. Connaître la taille et l’emplacement de l’ellipse, ainsi que les angles de début et de balayage, les points de début et de fin de l’arc peuvent être calculés à l’aide de trigonométrie simple :

x = oval.MidX + (oval.Width / 2) * cos(angle)

y = oval.MidY + (oval.Height / 2) * sin(angle)

La angle valeur est soit startAngle .startAngle + sweepAngle

L’utilisation de deux angles pour définir un arc est optimale pour les cas où vous connaissez la longueur angulaire de l’arc que vous souhaitez dessiner, par exemple pour créer un graphique en secteurs. La page Graphique en secteurs explosé illustre cela. La ExplodedPieChartPage classe utilise une classe interne pour définir des données et des couleurs fabriquées :

class ChartData
{
    public ChartData(int value, SKColor color)
    {
        Value = value;
        Color = color;
    }

    public int Value { private set; get; }

    public SKColor Color { private set; get; }
}

ChartData[] chartData =
{
    new ChartData(45, SKColors.Red),
    new ChartData(13, SKColors.Green),
    new ChartData(27, SKColors.Blue),
    new ChartData(19, SKColors.Magenta),
    new ChartData(40, SKColors.Cyan),
    new ChartData(22, SKColors.Brown),
    new ChartData(29, SKColors.Gray)
};

Le PaintSurface gestionnaire effectue d’abord une boucle dans les éléments pour calculer un totalValues nombre. À partir de là, elle peut déterminer la taille de chaque élément comme fraction du total et la convertir en angle :

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    int totalValues = 0;

    foreach (ChartData item in chartData)
    {
        totalValues += item.Value;
    }

    SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
    float explodeOffset = 50;
    float radius = Math.Min(info.Width / 2, info.Height / 2) - 2 * explodeOffset;
    SKRect rect = new SKRect(center.X - radius, center.Y - radius,
                             center.X + radius, center.Y + radius);

    float startAngle = 0;

    foreach (ChartData item in chartData)
    {
        float sweepAngle = 360f * item.Value / totalValues;

        using (SKPath path = new SKPath())
        using (SKPaint fillPaint = new SKPaint())
        using (SKPaint outlinePaint = new SKPaint())
        {
            path.MoveTo(center);
            path.ArcTo(rect, startAngle, sweepAngle, false);
            path.Close();

            fillPaint.Style = SKPaintStyle.Fill;
            fillPaint.Color = item.Color;

            outlinePaint.Style = SKPaintStyle.Stroke;
            outlinePaint.StrokeWidth = 5;
            outlinePaint.Color = SKColors.Black;

            // Calculate "explode" transform
            float angle = startAngle + 0.5f * sweepAngle;
            float x = explodeOffset * (float)Math.Cos(Math.PI * angle / 180);
            float y = explodeOffset * (float)Math.Sin(Math.PI * angle / 180);

            canvas.Save();
            canvas.Translate(x, y);

            // Fill and stroke the path
            canvas.DrawPath(path, fillPaint);
            canvas.DrawPath(path, outlinePaint);
            canvas.Restore();
        }

        startAngle += sweepAngle;
    }
}

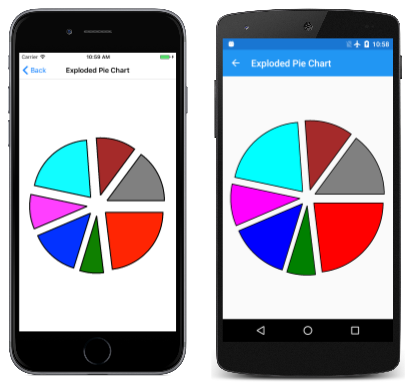
Un nouvel SKPath objet est créé pour chaque tranche de secteurs. Le chemin se compose d’une ligne du centre, puis d’une ArcTo ligne pour dessiner l’arc, et une autre ligne vers les résultats du centre à partir de l’appel Close . Ce programme affiche des tranches de secteurs « explosées » en les déplaçant toutes hors du centre de 50 pixels. Cette tâche nécessite un vecteur dans la direction du point intermédiaire de l’angle de balayage pour chaque tranche :

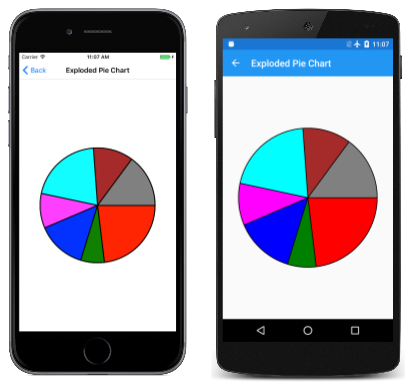
Pour voir ce qu’il semble sans l’explosion, il suffit de commenter l’appel Translate :

Arc tangente

Le deuxième type d’arc pris en charge par SKPath est l’arc tangent, appelé ainsi parce que l’arc est la circonférence d’un cercle qui est tangent à deux lignes connectées.

Un arc tangent est ajouté à un chemin d’accès avec un appel à la ArcTo méthode avec deux SKPoint paramètres, ou la ArcTo surcharge avec des paramètres distincts Single pour les points :

public void ArcTo (SKPoint point1, SKPoint point2, Single radius)

public void ArcTo (Single x1, Single y1, Single x2, Single y2, Single radius)

Cette ArcTo méthode est similaire à la fonction PostScript arct (page 532) et à la méthode iOS AddArcToPoint .

La ArcTo méthode implique trois points :

• Point actuel du contour ou point (0, 0) s’il MoveTo n’a pas été appelé
• Premier argument de point à la ArcTo méthode, appelé point d’angle
• Deuxième argument de point à ArcTo, appelé point de destination :

Ces trois points définissent deux lignes connectées :

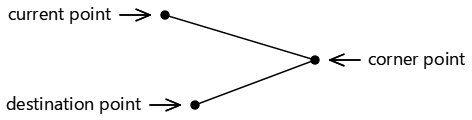
Si les trois points sont colignes, c’est-à-dire s’ils reposent sur la même ligne droite , aucun arc ne sera dessiné.

La ArcTo méthode inclut également un radius paramètre. Cela définit le rayon d’un cercle :

L’arc tangente n’est pas généralisé pour un ellipse.

Si les deux lignes se rencontrent à n’importe quel angle, ce cercle peut être inséré entre ces lignes afin qu’elle soit tangente aux deux lignes :

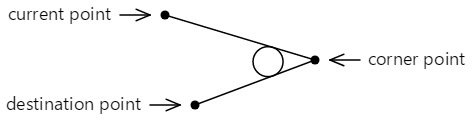
La courbe ajoutée au contour ne touche pas l’un des points spécifiés dans la ArcTo méthode. Il se compose d’une ligne droite du point actuel au premier point tangente et d’un arc qui se termine au deuxième point tangent, illustré ici en rouge :

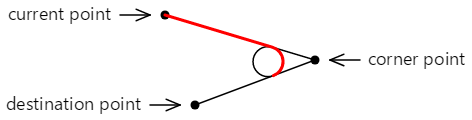
Voici la ligne droite finale et l’arc ajoutés au contour :

Le contour peut être continué à partir du deuxième point tangent.

La page Arc tangente vous permet d’expérimenter l’arc tangente. Il s’agit du premier de plusieurs pages qui dérivent de InteractivePage, qui définit quelques objets pratiques SKPaint et effectue le TouchPoint traitement :

public class InteractivePage : ContentPage
{
    protected SKCanvasView baseCanvasView;
    protected TouchPoint[] touchPoints;

    protected SKPaint strokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Black,
        StrokeWidth = 3
    };

    protected SKPaint redStrokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Red,
        StrokeWidth = 15
    };

    protected SKPaint dottedStrokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Black,
        StrokeWidth = 3,
        PathEffect = SKPathEffect.CreateDash(new float[] { 7, 7 }, 0)
    };

    protected void OnTouchEffectAction(object sender, TouchActionEventArgs args)
    {
        bool touchPointMoved = false;

        foreach (TouchPoint touchPoint in touchPoints)
        {
            float scale = baseCanvasView.CanvasSize.Width / (float)baseCanvasView.Width;
            SKPoint point = new SKPoint(scale * (float)args.Location.X,
                                        scale * (float)args.Location.Y);
            touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
        }

        if (touchPointMoved)
        {
            baseCanvasView.InvalidateSurface();
        }
    }
}

La classe TangentArcPage est dérivée de InteractivePage. Le constructeur du fichier TangentArcPage.xaml.cs est responsable de l’instanciation et de l’initialisation du touchPoints tableau, et de la définition baseCanvasView (inInteractivePage) de l’objet SKCanvasView instancié dans le fichier TangentArcPage.xaml :

public partial class TangentArcPage : InteractivePage
{
    public TangentArcPage()
    {
        touchPoints = new TouchPoint[3];

        for (int i = 0; i < 3; i++)
        {
            TouchPoint touchPoint = new TouchPoint
            {
                Center = new SKPoint(i == 0 ? 100 : 500,
                                     i != 2 ? 100 : 500)
            };
            touchPoints[i] = touchPoint;
        }

        InitializeComponent();

        baseCanvasView = canvasView;
        radiusSlider.Value = 100;
    }

    void sliderValueChanged(object sender, ValueChangedEventArgs args)
    {
        if (canvasView != null)
        {
            canvasView.InvalidateSurface();
        }
    }
    ...
}

Le PaintSurface gestionnaire utilise la méthode pour dessiner l’arc ArcTo en fonction des points tactiles et d’un Slider, mais calcule également le cercle sur lequel l’angle est basé :

public partial class TangentArcPage : InteractivePage
{
    ...
    void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
    {
        SKImageInfo info = args.Info;
        SKSurface surface = args.Surface;
        SKCanvas canvas = surface.Canvas;

        canvas.Clear();

        // Draw the two lines that meet at an angle
        using (SKPath path = new SKPath())
        {
            path.MoveTo(touchPoints[0].Center);
            path.LineTo(touchPoints[1].Center);
            path.LineTo(touchPoints[2].Center);
            canvas.DrawPath(path, dottedStrokePaint);
        }

        // Draw the circle that the arc wraps around
        float radius = (float)radiusSlider.Value;

        SKPoint v1 = Normalize(touchPoints[0].Center - touchPoints[1].Center);
        SKPoint v2 = Normalize(touchPoints[2].Center - touchPoints[1].Center);

        double dotProduct = v1.X * v2.X + v1.Y * v2.Y;
        double angleBetween = Math.Acos(dotProduct);
        float hypotenuse = radius / (float)Math.Sin(angleBetween / 2);
        SKPoint vMid = Normalize(new SKPoint((v1.X + v2.X) / 2, (v1.Y + v2.Y) / 2));
        SKPoint center = new SKPoint(touchPoints[1].Center.X + vMid.X * hypotenuse,
                                     touchPoints[1].Center.Y + vMid.Y * hypotenuse);

        canvas.DrawCircle(center.X, center.Y, radius, this.strokePaint);

        // Draw the tangent arc
        using (SKPath path = new SKPath())
        {
            path.MoveTo(touchPoints[0].Center);
            path.ArcTo(touchPoints[1].Center, touchPoints[2].Center, radius);
            canvas.DrawPath(path, redStrokePaint);
        }

        foreach (TouchPoint touchPoint in touchPoints)
        {
            touchPoint.Paint(canvas);
        }
    }

    // Vector methods
    SKPoint Normalize(SKPoint v)
    {
        float magnitude = Magnitude(v);
        return new SKPoint(v.X / magnitude, v.Y / magnitude);
    }

    float Magnitude(SKPoint v)
    {
        return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
    }
}

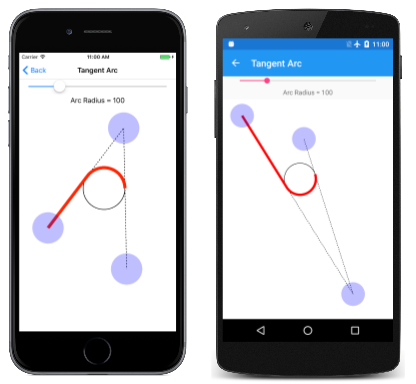
Voici la page Tangent Arc en cours d’exécution :

L’arc tangente est idéal pour créer des angles arrondis, tels qu’un rectangle arrondi. Étant donné qu’elle SKPath inclut déjà une AddRoundedRect méthode, la page Heptagon arrondie montre comment ArcTo arrondir les angles d’un polygone à sept côtés. (Le code est généralisé pour n’importe quel polygone normal.)

Le PaintSurface gestionnaire de la RoundedHeptagonPage classe contient une for boucle pour calculer les coordonnées des sept sommets du heptagon, et une seconde pour calculer les points intermédiaires des sept côtés de ces sommets. Ces points intermédiaires sont ensuite utilisés pour construire le chemin d’accès :

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    float cornerRadius = 100;
    int numVertices = 7;
    float radius = 0.45f * Math.Min(info.Width, info.Height);

    SKPoint[] vertices = new SKPoint[numVertices];
    SKPoint[] midPoints = new SKPoint[numVertices];

    double vertexAngle = -0.5f * Math.PI;       // straight up

    // Coordinates of the vertices of the polygon
    for (int vertex = 0; vertex < numVertices; vertex++)
    {
        vertices[vertex] = new SKPoint(radius * (float)Math.Cos(vertexAngle),
                                       radius * (float)Math.Sin(vertexAngle));
        vertexAngle += 2 * Math.PI / numVertices;
    }

    // Coordinates of the midpoints of the sides connecting the vertices
    for (int vertex = 0; vertex < numVertices; vertex++)
    {
        int prevVertex = (vertex + numVertices - 1) % numVertices;
        midPoints[vertex] = new SKPoint((vertices[prevVertex].X + vertices[vertex].X) / 2,
                                        (vertices[prevVertex].Y + vertices[vertex].Y) / 2);
    }

    // Create the path
    using (SKPath path = new SKPath())
    {
        // Begin at the first midpoint
        path.MoveTo(midPoints[0]);

        for (int vertex = 0; vertex < numVertices; vertex++)
        {
            SKPoint nextMidPoint = midPoints[(vertex + 1) % numVertices];

            // Draws a line from the current point, and then the arc
            path.ArcTo(vertices[vertex], nextMidPoint, cornerRadius);

            // Connect the arc with the next midpoint
            path.LineTo(nextMidPoint);
        }
        path.Close();

        // Render the path in the center of the screen
        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Blue;
            paint.StrokeWidth = 10;

            canvas.Translate(info.Width / 2, info.Height / 2);
            canvas.DrawPath(path, paint);
        }
    }
}

Voici le programme en cours d’exécution :

Arc elliptique

L’arc elliptique est ajouté à un chemin d’accès avec un appel à la ArcTo méthode qui a deux SKPoint paramètres, ou la ArcTo surcharge avec des coordonnées X et Y distinctes :

public void ArcTo (SKPoint r, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, SKPoint xy)

public void ArcTo (Single rx, Single ry, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, Single x, Single y)

L’arc elliptique est cohérent avec l’arc elliptique inclus dans Scalable Vector Graphics (SVG) et la classe plateforme Windows universelleArcSegment.

Ces ArcTo méthodes dessinent un arc entre deux points, qui sont le point actuel du contour et le dernier paramètre de la ArcTo méthode (le paramètre ou les xy paramètres distincts x et y les paramètres) :

Le premier paramètre de point de la ArcTo méthode (rou et ryrx ) n’est pas un point du tout, mais spécifie plutôt le rayon horizontal et vertical d’un ellipse ;

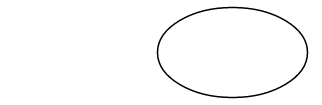
Le xAxisRotate paramètre est le nombre de degrés d’horloge à faire pivoter cette ellipse :

Si cette ellipse inclinée est alors positionnée de sorte qu’elle touche les deux points, les points sont connectés par deux arcs différents :

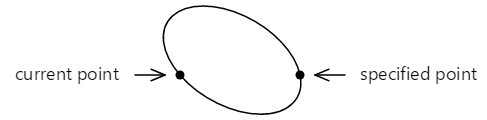
Ces deux arcs peuvent être distingués de deux manières : l’arc supérieur est supérieur à l’arc inférieur, et comme l’arc est dessiné de gauche à droite, l’arc supérieur est dessiné dans une direction dans le sens des aiguilles d’une montre tandis que l’arc inférieur est dessiné dans une direction à sens inverse.

Il est également possible d’ajuster l’ellipse entre les deux points d’une autre manière :

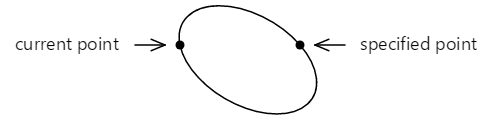
Maintenant, il y a un arc plus petit sur le dessus qui est dessiné dans le sens des aiguilles d’une montre, et un arc plus grand sur le bas qui est dessiné dans le sens inverse des aiguilles d’une montre.

Ces deux points peuvent donc être connectés par un arc défini par l’ellipse inclinée de quatre façons :

Ces quatre arcs sont distingués par les quatre combinaisons des arguments de type d’énumération et SKPathDirection de la SKPathArcSize ArcTo méthode :

• rouge : SKPathArcSize.Large et SKPathDirection.Clockwise
• vert : SKPathArcSize.Small et SKPathDirection.Clockwise
• blue : SKPathArcSize.Small et SKPathDirection.CounterClockwise
• magenta : SKPathArcSize.Large et SKPathDirection.CounterClockwise

Si l’ellipse inclinée n’est pas assez grande pour s’ajuster entre les deux points, elle est uniformément mise à l’échelle jusqu’à ce qu’elle soit assez grande. Seuls deux arcs uniques connectent les deux points dans ce cas. Ceux-ci peuvent être distingués par le SKPathDirection paramètre.

Bien que cette approche de la définition d’un arc sonne complexe lors de la première rencontre, il s’agit de la seule approche qui permet de définir un arc avec un ellipse pivoté, et c’est souvent l’approche la plus simple lorsque vous devez intégrer des arcs à d’autres parties du contour.

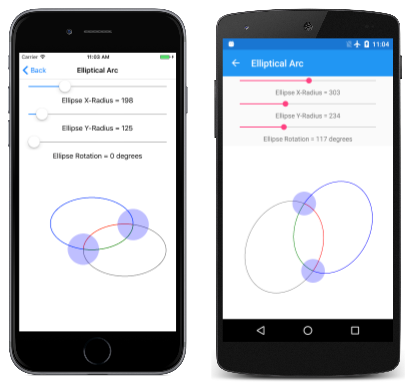
La page Arc Elliptical vous permet de définir de manière interactive les deux points, ainsi que la taille et la rotation de l’ellipse. La EllipticalArcPage classe dérive de InteractivePage, et le PaintSurface gestionnaire dans le fichier code-behind EllipticalArcPage.xaml.cs dessine les quatre arcs :

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    using (SKPath path = new SKPath())
    {
        int colorIndex = 0;
        SKPoint ellipseSize = new SKPoint((float)xRadiusSlider.Value,
                                          (float)yRadiusSlider.Value);
        float rotation = (float)rotationSlider.Value;

        foreach (SKPathArcSize arcSize in Enum.GetValues(typeof(SKPathArcSize)))
            foreach (SKPathDirection direction in Enum.GetValues(typeof(SKPathDirection)))
            {
                path.MoveTo(touchPoints[0].Center);
                path.ArcTo(ellipseSize, rotation,
                           arcSize, direction,
                           touchPoints[1].Center);

                strokePaint.Color = colors[colorIndex++];
                canvas.DrawPath(path, strokePaint);
                path.Reset();
            }
    }

    foreach (TouchPoint touchPoint in touchPoints)
    {
        touchPoint.Paint(canvas);
    }
}

Ici, il est en cours d’exécution :

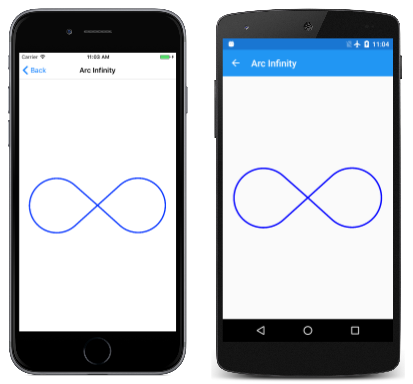
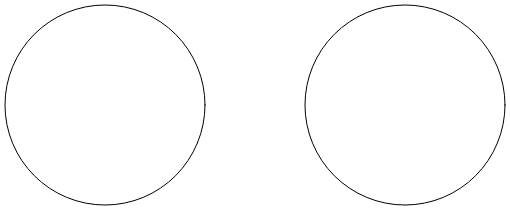
La page Arc Infinity utilise l’arc elliptique pour dessiner un signe infini. Le signe infini est basé sur deux cercles avec rayon de 100 unités séparées par 100 unités :

Deux lignes se croisant sont tangentes aux deux cercles :

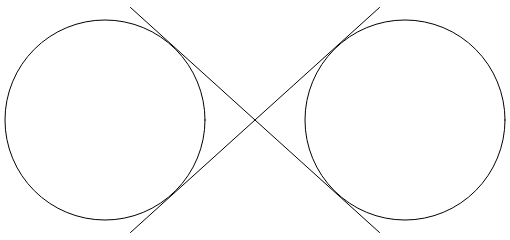
Le signe infini est une combinaison de parties de ces cercles et des deux lignes. Pour utiliser l’arc elliptique pour dessiner le signe infini, les coordonnées où les deux lignes sont tangentes aux cercles doivent être déterminées.

Construisez un rectangle droit dans l’un des cercles :

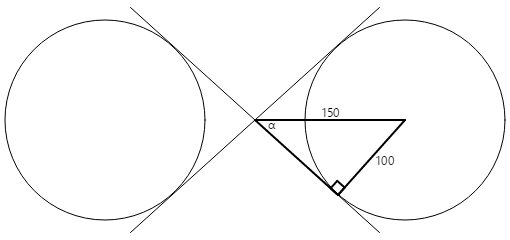
Le rayon du cercle est de 100 unités et l’hypotenuse du triangle est de 150 unités, de sorte que l’angle α est l’arcsine (sinus inverse) de 100 divisé par 150 ou 41,8 degrés. La longueur de l’autre côté du triangle est de 150 fois le cosinus de 41,8 degrés, ou 112, qui peut également être calculé par le théorème pythagorean.

Les coordonnées du point tangent peuvent ensuite être calculées à l’aide de ces informations :

x = 112·cos(41.8) = 83

y = 112·sin(41.8) = 75

Les quatre points tangentes sont tout ce qui est nécessaire pour dessiner un signe infini centré sur le point (0, 0) avec rayon du cercle de 100 :

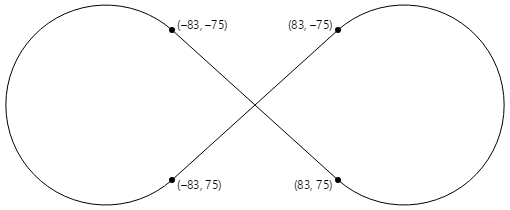
Le PaintSurface gestionnaire de la ArcInfinityPage classe positionne le signe infini afin que le point (0, 0) soit positionné au centre de la page et met à l’échelle le chemin d’accès à la taille de l’écran :

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    using (SKPath path = new SKPath())
    {
        path.LineTo(83, 75);
        path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.CounterClockwise, 83, -75);
        path.LineTo(-83, 75);
        path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.Clockwise, -83, -75);
        path.Close();

        // Use path.TightBounds for coordinates without control points
        SKRect pathBounds = path.Bounds;

        canvas.Translate(info.Width / 2, info.Height / 2);
        canvas.Scale(Math.Min(info.Width / pathBounds.Width,
                              info.Height / pathBounds.Height));

        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Blue;
            paint.StrokeWidth = 5;

            canvas.DrawPath(path, paint);
        }
    }
}

Le code utilise la Bounds propriété de SKPath déterminer les dimensions du sinus infini pour l’adapter à la taille du canevas :

Le résultat semble un peu petit, ce qui suggère que la Bounds propriété d’est SKPath signaler une taille supérieure au chemin d’accès.

En interne, Skia se rapproche de l’arc à l’aide de plusieurs courbes quadratiques de Bézier. Ces courbes (comme vous le verrez dans la section suivante) contiennent des points de contrôle qui régissent la façon dont la courbe est dessinée, mais qui ne font pas partie de la courbe rendue. La Bounds propriété inclut ces points de contrôle.

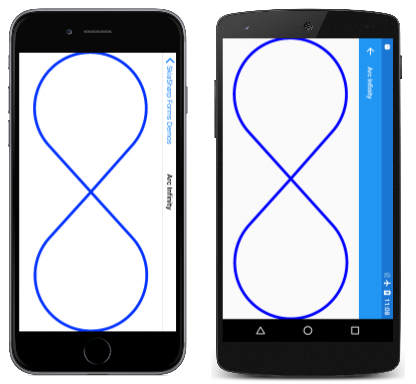
Pour obtenir un ajustement plus serré, utilisez la TightBounds propriété, qui exclut les points de contrôle. Voici le programme s’exécutant en mode paysage et en utilisant la TightBounds propriété pour obtenir les limites de chemin d’accès :

Bien que les connexions entre les arcs et les lignes droites soient mathématiquement lisses, le passage de l’arc à la ligne droite peut sembler un peu abrupt. Un meilleur signe infini est présenté dans l’article suivant sur trois types de courbes de Bézier.

Liens associés

• API SkiaSharp