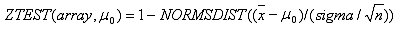Méthode WorksheetFunction.ZTest (Excel)
Renvoie la valeur de probabilité à un point d’un test z. Pour une moyenne de population hypothétique donnée, ZTest renvoie la probabilité que la moyenne de l’échantillon soit supérieure à la moyenne des observations dans le jeu de données (tableau) ; autrement dit, la moyenne de l’échantillon observé.
Importante
Cette fonction a été remplacée par de nouvelles fonctions qui peuvent fournir une meilleure précision et dont les noms reflètent mieux leur utilisation. Cette fonction est toujours disponible pour assurer la compatibilité avec les versions antérieures d’Excel. Toutefois, si la compatibilité descendante n'est pas requise, vous devriez envisager d'utiliser les nouvelles fonctions à partir de maintenant, car elles décrivent plus précisément leur usage.
Pour plus d’informations sur la nouvelle fonction, consultez la méthode Z_Test .
Syntaxe
expression. ZTest (Arg1, Arg2, Arg3)
Expression Variable qui représente un objet WorksheetFunction .
Parameters
| Nom | Requis/Facultatif | Type de données | Description |
|---|---|---|---|
| Arg1 | Obligatoire | Variant | Array est la matrice ou la plage de données par rapport à laquelle tester la moyenne de population hypothétique. |
| Arg2 | Obligatoire | Double | Valeur à tester. |
| Arg3 | Facultatif | Variant | Sigma est l’écart type de population (connu). Si cette valeur est omise, l’écart-type de l’échantillon est utilisé. |
Valeur renvoyée
Double
Remarques
Si array est vide, ZTest renvoie la valeur d’erreur #N/A.
ZTest est calculé comme suit lorsque sigma n’est pas omis :
ZTest est calculé comme suit lorsque sigma est omis, où x est la moyenne moyenne de l’échantillon(tableau), s est l’écart type STDEV(tableau) et n est le nombre d’observations dans l’échantillon COUNT(array) :
ZTest représente la probabilité que la moyenne de l’échantillon soit supérieure à la valeur observée AVERAGE(matrice), lorsque la moyenne de population sous-jacente est μ0. À partir de la symétrie de la distribution normale, si AVERAGE(array) < μ0, ZTest retourne une valeur supérieure à 0,5.
La formule Excel suivante peut être utilisée pour calculer la probabilité à deux extrémités que la moyenne de l’échantillon soit plus éloignée de μ0 (dans les deux sens) que MOYENNE (tableau), lorsque la moyenne de population sous-jacente est de μ0 :
=2 * MIN(ZTEST(_array_,μ0,_sigma_), 1 - ZTEST(_array_,μ0,_sigma_)).
Assistance et commentaires
Avez-vous des questions ou des commentaires sur Office VBA ou sur cette documentation ? Consultez la rubrique concernant l’assistance pour Office VBA et l’envoi de commentaires afin d’obtenir des instructions pour recevoir une assistance et envoyer vos commentaires.