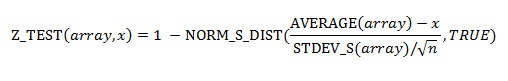méthode WorksheetFunction.Z_Test (Excel)
Renvoie la valeur de probabilité à un point d’un test z. Pour une moyenne de population hypothétique donnée, Z_Test renvoie la probabilité que la moyenne de l’échantillon soit supérieure à la moyenne des observations dans le jeu de données (tableau); autrement dit, la moyenne de l’échantillon observé.
Syntaxe
expression. Z_Test (Arg1, Arg2, Arg3)
Expression Variable qui représente un objet WorksheetFunction .
Parameters
| Nom | Requis/Facultatif | Type de données | Description |
|---|---|---|---|
| Arg1 | Obligatoire | Variant | Array est la matrice ou la plage de données par rapport à laquelle tester la moyenne de population hypothétique. |
| Arg2 | Obligatoire | Double | Valeur à tester. |
| Arg3 | Facultatif | Variant | Sigma est l’écart type de population (connu). Si cette valeur est omise, l’écart-type de l’échantillon est utilisé. |
Valeur renvoyée
Double
Remarques
Si array est vide, Z_Test retourne la valeur d’erreur #N/A.
Z_Test est calculé comme suit lorsque sigma n’est pas omis :
Z_Test est calculé comme suit lorsque sigma est omis, où x est l’exemple moyen moyen(tableau) ; s est l’exemple d’écart type STDEV_S(tableau); et n est le nombre d’observations dans l’exemple COUNT(array) :
Z_Test représente la probabilité que la moyenne de l’échantillon soit supérieure à la valeur observée AVERAGE(matrice), lorsque la moyenne de population sous-jacente est μ0. À partir de la symétrie de la distribution normale, si MOYENNE(matrice) < μ0, Z_Test retournera une valeur supérieure à 0,5.
La formule Excel suivante peut être utilisée pour calculer la probabilité à deux extrémités que la moyenne de l’échantillon soit plus éloignée de μ0 (dans les deux sens) que MOYENNE (tableau), lorsque la moyenne de population sous-jacente est de μ0 :
=2 * MIN(Z_TEST(_array_,μ0,_sigma_), 1 - Z_TEST(_array_,μ0,_sigma_))
Assistance et commentaires
Avez-vous des questions ou des commentaires sur Office VBA ou sur cette documentation ? Consultez la rubrique concernant l’assistance pour Office VBA et l’envoi de commentaires afin d’obtenir des instructions pour recevoir une assistance et envoyer vos commentaires.