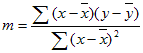Méthode WorksheetFunction.LinEst (Excel)

Calcule les statistiques d’une ligne à l’aide de la méthode des moindres carrés pour calculer une ligne droite qui correspond le mieux à vos données et retourne un tableau qui décrit la ligne. Comme cette fonction renvoie une matrice de valeurs, elle doit être entrée sous forme de formule matricielle.

Syntaxe

expression. LinEst (Arg1, Arg2, Arg3, Arg4)

Expression Variable qui représente un objet WorksheetFunction .

Parameters

Nom	Requis/Facultatif	Type de données	Description
Arg1	Obligatoire	Variant	Known_y : ensemble de valeurs y que vous connaissez déjà dans la relation y = mx + b.
Arg2	Facultatif	Variante	x_connus - ensemble de valeurs x facultatives que vous connaissez peut-être déjà dans la relation y = mx + b.
Arg3	Facultatif	Variante	Const - valeur logique indiquant si la constante b doit être forcée pour être égale à 0.
Arg4	Facultatif	Variante	Stats - valeur logique qui spécifie si des statistiques de régression supplémentaires doivent être renvoyées.

Valeur renvoyée

Variant

Remarques

L’équation de la ligne est y = mx + b ou y = m1x1 + m2x2 + ... + b (s’il existe plusieurs plages de valeurs x), où la valeur y dépendante est une fonction des valeurs x indépendantes. Les valeurs_m sont des coefficients correspondant à chaque valeur x et b est une valeur constante. Notez que x, y et m peuvent être des vecteurs. Le tableau retourné par LinEst est {mn,mn-1,...,m1,b}. LinEst peut également retourner des statistiques de régression supplémentaires.

Si le tableau de known_y se trouve dans une seule colonne, chaque colonne de known_x est interprétée comme une variable distincte.

Si le tableau de known_y se trouve dans une seule ligne, chaque ligne de known_x est interprétée comme une variable distincte.

La matrice x_connus peut inclure un ou plusieurs ensembles de variables. Si une seule variable est utilisée, les matrices y_connus et x_connus peuvent être des plages de valeurs de toute forme, tant que leurs dimensions sont égales. Si plusieurs variables sont utilisées, la matrice y_connus doit être un vecteur (c'est-à-dire, une plage de valeurs avec une hauteur d'une ligne ou une largeur d'une colonne).

Si known_x est omis, il est supposé qu’il s’agit du tableau {1,2,3,...} de la même taille que known_y.

• Si const a la valeur True ou omise, b est calculé normalement.

• Si const a la valeur False, b est défini sur 0 et les valeurs m sont ajustées pour s’adapter y = mxà .

• Si les statistiques ont la valeur True, LinEst retourne les statistiques de régression supplémentaires, de sorte que le tableau retourné est {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}.

• Si les statistiques ont la valeur False ou sont omises, LinEst retourne uniquement les coefficients m et la constante b.

Les statistiques de régression supplémentaires sont les suivantes :

Statistique de régression	Description
se1,se2,...,sen	Les valeurs d'erreur type pour les coefficients m1,m2,...,mn.
seb	Valeur d’erreur standard pour la constante b (seb = #N/A quand const a la valeur False).
R2	Coefficient de détermination. Compare les valeurs y estimées et réelles, et les plages de valeur comprises entre 0 et 1. S’il est 1, il existe une corrélation parfaite dans l’échantillon : il n’y a aucune différence entre la valeur y estimée et la valeur y réelle. À l’autre extrême, si le coefficient de détermination est 0, l’équation de régression n’est pas utile pour prédire une valeur y.
sey	L'erreur type pour l'estimation de y.
F	La statistique F ou valeur F observée. Utilisez la statistique F pour déterminer si la relation observée entre les variables dépendantes et les variables indépendantes est le fruit du hasard.
df	Les degrés de liberté. Utilisez les degrés de liberté pour vous aider à trouver les valeurs critiques F dans un tableau de statistiques. Comparez les valeurs que vous trouvez dans la table à la statistique F retournée par LinEst pour déterminer un niveau de confiance pour le modèle.
ssreg	La somme des carrés de régression.
ssresid	La somme des carrés résiduelle.

L'illustration ci-dessous indique l'ordre dans lequel les statistiques de régression supplémentaires sont renvoyées.

Vous pouvez décrire n’importe quelle ligne droite avec la pente et l’intercept y : Slope (m). Pour trouver la pente d’une ligne, souvent écrite sous la forme m, prenez deux points sur la ligne, (x1,y1) et (x2,y2); la pente est égale à (y2 - y1)/(x2 - x1). Intercepte Y (b) : l’interception y d’une ligne, souvent écrite sous la forme b, est la valeur de y au point où la ligne traverse l’axe y. L'équation d'une droite est y = mx + b. Une fois que vous connaissez les valeurs de m et b, vous pouvez calculer n’importe quel point sur la ligne en branchant la valeur y ou x dans cette équation. Vous pouvez également utiliser la fonction TREND.

Lorsque vous n’avez qu’une seule variable x indépendante, vous pouvez obtenir les valeurs de pente et d’interception y directement à l’aide des formules suivantes :

• Pente: =INDEX(LINEST(known_y's,known_x's),1)
• Interception Y : =INDEX(LINEST(known_y's,known_x's),2)

La précision de la ligne calculée par LinEst dépend du degré de nuage de points dans vos données. Plus les données sont linéaires, plus le modèle LinEst est précis. LinEst utilise la méthode des moindres carrés pour déterminer le meilleur ajustement pour les données. Lorsque vous ne disposez qu'une variable x indépendante, le calcul de m et de b se base sur les formules suivantes :

où x et y sont des moyennes d’échantillon, c’est-à-dire x = MOYENNE(x connus) et y = MOYENNE(known_y).

Les fonctions d’ajustement de courbe et de courbe LinEst et LogEst peuvent calculer la meilleure courbe droite ou exponentielle qui correspond à vos données. Cependant, vous devez déterminer le résultat qui est le plus ajusté à vos données. Vous pouvez calculer TREND(known_y's,known_x's) pour une ligne droite ou GROWTH(known_y's, known_x's) pour une courbe exponentielle. Ces fonctions, sans l'argument nouvel x, renvoient une matrice de valeurs y prévues sur cette droite ou cette courbe à vos points de données réels. Vous pouvez comparer les valeurs prévues avec les valeurs réelles. Vous pouvez les représenter graphiquement pour effectuer une comparaison visuelle.

Dans l’analyse de régression, Microsoft Excel calcule pour chaque point la différence quadratique entre la valeur y estimée pour ce point et sa valeur y réelle. La somme de ces différences carrées est appelée somme résiduelle de carrés, ssresid. Excel calcule ensuite la somme totale des carrés, sstotal. Lorsque const = TRUE, ou omis, la somme totale des carrés est la somme des différences au carré entre les valeurs y réelles et la moyenne des valeurs y. Lorsque const = FALSE, la somme totale des carrés est la somme des carrés des valeurs y réelles (sans soustraire la valeur y moyenne de chaque valeur y individuelle). Ensuite, la somme de régression des carrés, ssreg, est disponible à partir de ssreg = sstotal - ssresid. Plus la somme résiduelle des carrés est petite par rapport à la somme totale des carrés, plus la valeur du coefficient de détermination, r2, est grande, ce qui est un indicateur de la façon dont l’équation résultant de l’analyse de régression explique la relation entre les variables; r2 est égal à ssreg/sstotal.

Dans certains cas, une ou plusieurs colonnes X (supposons que Y et X se trouvent dans des colonnes) peuvent n’avoir aucune valeur prédictive supplémentaire en présence des autres colonnes X. En d'autres termes, la suppression d'une ou de plusieurs colonnes X peut permettre d'obtenir des valeurs Y avec une précision égale. Dans ce cas, ces colonnes X redondantes doivent être omises du modèle de régression. Ce phénomène est appelé collinearité , car toute colonne X redondante peut être exprimée sous la forme d’une somme de multiples des colonnes X non redondantes. LinEst vérifie la collinearité et supprime toutes les colonnes X redondantes du modèle de régression lorsqu’il les identifie. Les colonnes X supprimées peuvent être reconnues dans la sortie LinEst comme ayant 0 coefficients, ainsi que 0 se.

• Si une ou plusieurs colonnes sont supprimées comme redondantes, df est affecté, car df dépend du nombre de colonnes X réellement utilisées à des fins prédictives. Si df est modifié parce que des colonnes X sont supprimées, la valeur de sey et de F est également affectée.
• Dans la pratique, la colinéarité est relativement rare. Toutefois, un cas où cela est le plus probable est lorsque certaines colonnes X contiennent uniquement 0 et 1 comme indicateurs indiquant si un sujet d’une expérience est ou non membre d’un groupe particulier. Si const = TRUE ou omis, LinEst insère effectivement une colonne X supplémentaire des 1 pour modéliser l’intercept. Si vous avez une colonne avec un 1 pour chaque sujet s’il est masculin, ou 0 si ce n’est pas le cas, et que vous avez également une colonne avec un 1 pour chaque sujet si une femme, ou 0 si ce n’est pas le cas, cette dernière colonne est redondante, car les entrées qu’elle contient peuvent être obtenues en soustrayant l’entrée dans la colonne d’indicateur masculin de l’entrée dans la colonne supplémentaire de tous les 1 ajoutés par LinEst.
• df est calculé comme suit quand aucune colonne X n’est supprimée du modèle en raison de la collinearité : s’il existe k colonnes de known_x et const = TRUE ou omis, df = n - k - 1. Si const = FALSE, df = n - k. Dans les deux cas, chaque colonne X supprimée en raison de la collinearité augmente df de 1.

Les formules qui renvoient des matrices doivent être saisies sous forme de formules matricielles.

• Lorsque vous entrez une constante matricielle comme x_connus comme argument, utilisez des virgules pour séparer les valeurs sur la même ligne et des points-virgules pour séparer les lignes. Les caractères de séparation peuvent être différents en fonction des paramètres régionaux et linguistiques définis dans Options régionales et linguistiques, dans le Panneau de configuration.
• Notez que les valeurs y prévues par l'équation de régression peuvent être incorrectes si elles se trouvent en dehors de la plage de valeurs y utilisées pour déterminer l'équation.

L’algorithme sous-jacent utilisé dans la fonction LinEst est différent de l’algorithme sous-jacent utilisé dans les fonctions Pente et Intercept . La différence entre ces algorithmes peut conduire à des résultats différents lorsque les données ne sont pas déterminées et qu'elles sont colinéaires. Par exemple, si les points de données de l'argument y_connus prennent la valeur 0 et que ceux de l'argument y_connus prennent la valeur 1 :

• LinEst retourne la valeur 0. L’algorithme LinEst est conçu pour retourner des résultats raisonnables pour les données collineaires, et dans ce cas, au moins une réponse peut être trouvée.
• Pente et Interception renvoient un #DIV/0! Erreur. L’algorithme Slope and Intercept est conçu pour rechercher une seule réponse, et dans ce cas, il peut y avoir plusieurs réponses.

Assistance et commentaires

Avez-vous des questions ou des commentaires sur Office VBA ou sur cette documentation ? Consultez la rubrique concernant l’assistance pour Office VBA et l’envoi de commentaires afin d’obtenir des instructions pour recevoir une assistance et envoyer vos commentaires.