series_fit_poly()
S’applique à : ✅Microsoft Fabric✅Azure Data Explorer✅Azure Monitor✅Microsoft Sentinel
Applique une régression polynomiale d’une variable indépendante (x_series) à une variable dépendante (y_series). Cette fonction prend une table contenant plusieurs séries (tableaux numériques dynamiques) et génère le meilleur polynomial d’ordre élevé pour chaque série à l’aide de la régression polynomiale.
Conseil
- Pour la régression linéaire d’une série uniformément espaquée, telle qu’elle est créée par l’opérateur make-series, utilisez la fonction plus simple series_fit_line(). Voir l’exemple 2.
- Si x_series est fourni et que la régression est effectuée pour un degré élevé, envisagez de normaliser la plage [0-1]. Voir l’exemple 3.
- Si x_series est de type datetime, il doit être converti en double et normalisé. Voir l’exemple 3.
- Pour obtenir une implémentation de référence de régression polynomiale à l’aide de Python inline, consultez series_fit_poly_fl().
Syntaxe
T | extend series_fit_poly( y_series [ , x_series , degré ])
En savoir plus sur les conventions de syntaxe.
Paramètres
| Nom | Type | Requise | Description |
|---|---|---|---|
| y_series | dynamic |
✔️ | Tableau de valeurs numériques contenant la variable dépendante. |
| x_series | dynamic |
Tableau de valeurs numériques contenant la variable indépendante. Obligatoire uniquement pour les séries espaquées de manière inégale. S’il n’est pas spécifié, il est défini sur une valeur par défaut de [1, 2, ..., length(y_series)]. | |
| degré | Ordre requis de la polynomiale à ajuster. Par exemple, 1 pour la régression linéaire, 2 pour la régression quadratique, et ainsi de suite. La valeur par défaut est 1, ce qui indique la régression linéaire. |
Retours
La series_fit_poly() fonction retourne les colonnes suivantes :
rsquare: r-square est une mesure standard de la qualité de l’ajustement. La valeur est un nombre dans la plage [0-1], où 1 - est le meilleur ajustement possible, et 0 signifie que les données sont non ordonnées et ne correspondent à aucune ligne.coefficients: tableau numérique contenant les coefficients du polynomial le mieux adapté avec le degré donné, classé du coefficient de puissance le plus élevé au plus bas.variance: variance de la variable dépendante (y_series).rvariance: variance résiduelle qui correspond à la variance entre les valeurs de données d’entrée les valeurs approximatives.poly_fit: tableau numérique contenant une série de valeurs du polynomial le mieux adapté. La longueur de la série est égale à la longueur de la variable dépendante (y_series). Valeur utilisée pour le graphique.
Exemples
Exemple 1
Polynomial de cinquième ordre avec bruit sur les axes x &y :
range x from 1 to 200 step 1
| project x = rand()*5 - 2.3
| extend y = pow(x, 5)-8*pow(x, 3)+10*x+6
| extend y = y + (rand() - 0.5)*0.5*y
| summarize x=make_list(x), y=make_list(y)
| extend series_fit_poly(y, x, 5)
| project-rename fy=series_fit_poly_y_poly_fit, coeff=series_fit_poly_y_coefficients
|fork (project x, y, fy) (project-away x, y, fy)
| render linechart
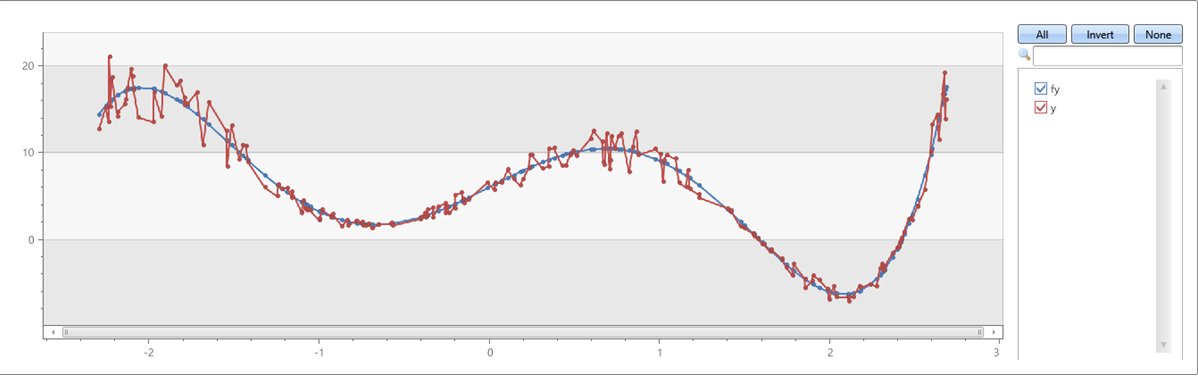
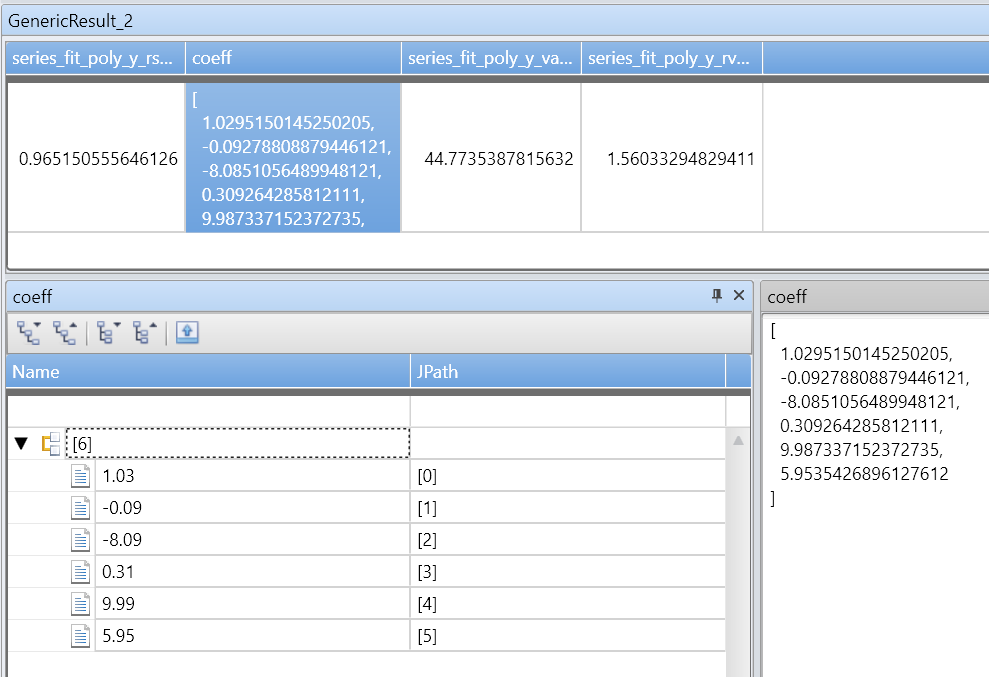
Exemple 2
Vérifiez qu’avec series_fit_poly degree=1 correspond series_fit_lineà :
demo_series1
| extend series_fit_line(y)
| extend series_fit_poly(y)
| project-rename y_line = series_fit_line_y_line_fit, y_poly = series_fit_poly_y_poly_fit
| fork (project x, y, y_line, y_poly) (project-away id, x, y, y_line, y_poly)
| render linechart with(xcolumn=x, ycolumns=y, y_line, y_poly)
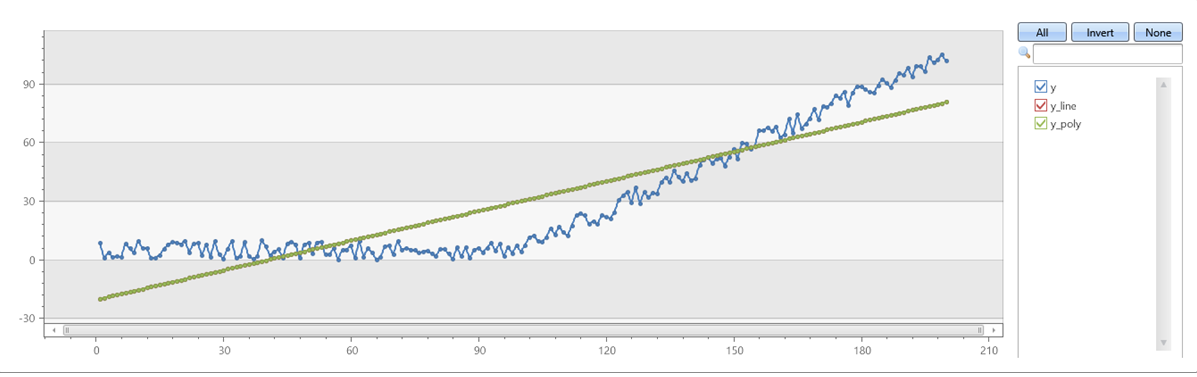

Exemple 3
Série chronologique irrégulière (inégalement espaquée) :
//
// x-axis must be normalized to the range [0-1] if either degree is relatively big (>= 5) or original x range is big.
// so if x is a time axis it must be normalized as conversion of timestamp to long generate huge numbers (number of 100 nano-sec ticks from 1/1/1970)
//
// Normalization: x_norm = (x - min(x))/(max(x) - min(x))
//
irregular_ts
| extend series_stats(series_add(TimeStamp, 0)) // extract min/max of time axis as doubles
| extend x = series_divide(series_subtract(TimeStamp, series_stats__min), series_stats__max-series_stats__min) // normalize time axis to [0-1] range
| extend series_fit_poly(num, x, 8)
| project-rename fnum=series_fit_poly_num_poly_fit
| render timechart with(ycolumns=num, fnum)