Small Basic: Centres de Rotation pour les Formes Triangle et Ligne (fr-FR)
Dans le langage de programmation Small Basic, l'objet Shapes possède l'opération Rotate. Les centres de Rotation pour les Rectangles et les Ellipses sont les centres des formes. Toutefois pour les Triangles et les Lignes, les centres de rotation ne sont pas toujours les centres des formes. Cet article traite des centres de rotation pour les Triangles et les Lignes. A savoir que cet article n'est valable que pour les programmes locaux (compilés dans l'EDI Small Basic).
Définition des coordonnées pour les Triangles et les Lignes
Les Rectangles et les Ellipses n'ont pas de positions mais ont une taille. Les Triangles et les Lignes sont définis comme ci-dessous avec les coordonnées de leur points.
- Shapes.AddTriangle(x1, y1, x2, y2, x3, y3)
- Shapes.AddLine(x1, y1, x2, y2)
Ces coordonnées détermine le centre de rotation. La règle typique pour un centre de rotation ne peut pas être négatif dans la définition des cordonnées. Il est toujours positif ou zéro.
Modèles avec des Porgrammes d'Exemple
Les programmes qui suivent calculent les centres de rotation et les affichent par une croix rouge. L'utilisation de ces programme est de cliquer pour définir les sommets pour les triangles ou les points de terminaison pour les lignes.
- Rotate Triangle 0.1 (CNM748) - exemple de programme pour la rotation de forme triangle
- Rotate Line 0.1 (KSL776) - exemple de programme pour la rotation de forme ligne
Centre du Rectangle Circonscrit d'une Forme
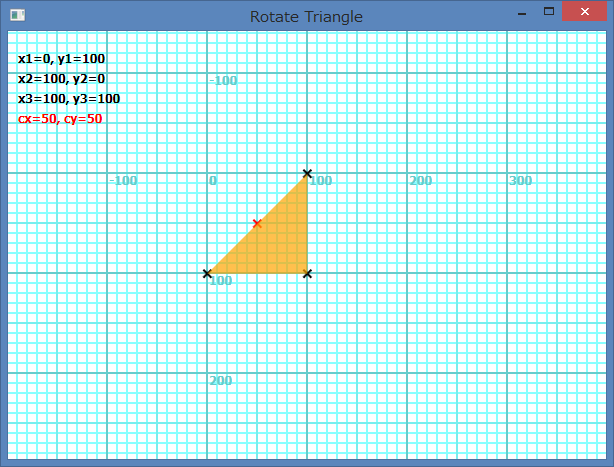
Si tous les sommets ne sont pas négatifs (inclus les zéros) pour chaque x et y dans la définition des coordonnées, le centre de rootation de la forme et le centre du rectangle circonscrit de la forme. L'image suivante montre le cas de Shapes.AddTriangle(0, 100, 100, 0, 100, 100). Son centre de rotation devient (50, 50).
Centre du Rectangle Circonscrit d'une Forme ou de l'Origine
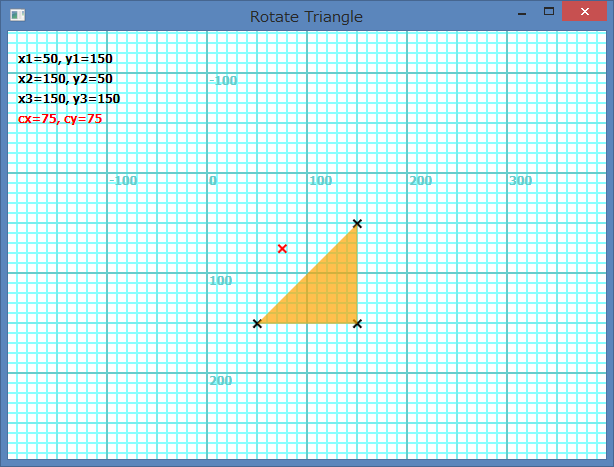
Si tous les sommets ne sont pas négatifs (inclus aucun ou un seul zéro) pour x ou y dans la définition des coordonnées, le centre de rotation de la forme est le centre du rectangle circonscrit de la forme et de l'origine de la définition des coordonnées. L'image suivante monte le cas de Shapes.AddTriangle(50, 150, 150, 50, 150, 150). Le centre de rotation devient (75, 75).
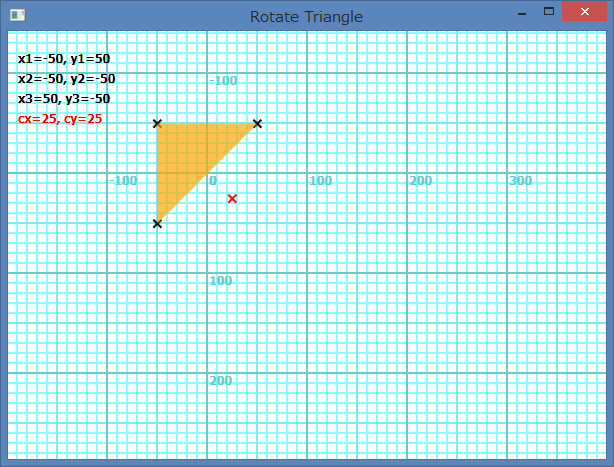
Si les sommets sont négatifs et négatifs dans la définition des coordonnées, le centre de rotation est le centre du rectangle de la partie positive du rectangle circonscrit de la forme. L'image suivante montre le cas de Shapes.AddTriangle(-50, 50, -50, -50, 50, -50). Le centre de rotation devient (25, 25).
Origine de la Forme Définie
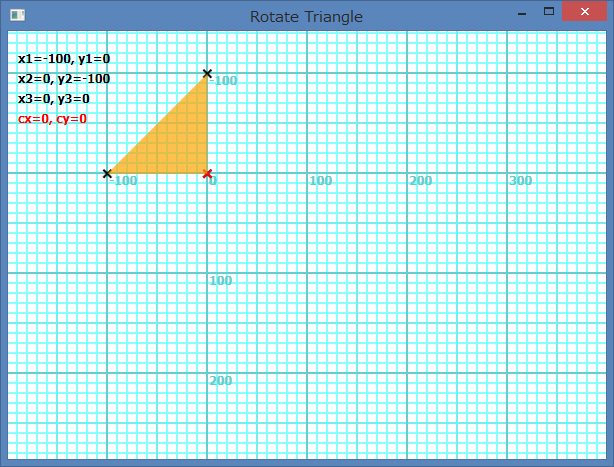
Si tous les sommets sont négatigs ou zéros dans la définition des coordonnées, le centre de rotation de la forme et l'origine de la définition des coordonnées. L'image suivante montre le cas de Shapes.AddTriangle(100, 0, 0, 100, 0, 0). Le centre de rotation devient (0, 0).
Sur l'Axe X ou l'Axe Y
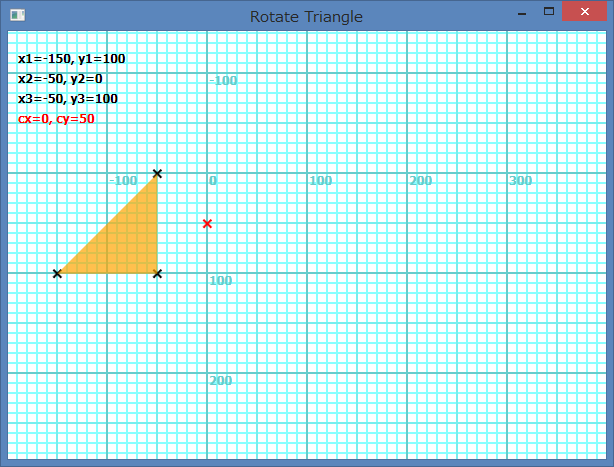
Si tous les sommets ne sont pas négatifs dans la définition des coordonnées, le centre de rotation de la forme est sur l'axe X ou l'axe Y. L'image suivante montre le cas de Shapes.AddTriangle(-150, 100, -50, 0, -50, 100). Le centre de rotation devient (0, 50).
Voir Aussi
- Small Basic: How to Rotate a Shape Not from the Center (a propos des Rectangles et des Ellipses) (en-US)
- Small Basic Known Issue: 27122 - Shapes.Rotate() Rotates Triangle and Line at Center in Local But at Corner in Remote (en-US)
Autres Langues
- Article original : Small Basic: Rotation Centers for Shapes of Triangle and Line