À la découverte de DAG

Article
11/17/2011

Article d’origine publié le vendredi 16 septembre 2011

Définitions

Nous savons tous que dans l’univers de Microsoft Exchange, l’acronyme DAG correspond à « Database Availability Group », à savoir « Groupe de disponibilité de base de données ».

Base de données – Sur un serveur de boîte aux lettres Exchange 2010 hautement disponible, la base de données (et non le serveur) est l’unité de disponibilité et peut faire l’objet d’un basculement entre plusieurs serveurs d’un groupe de disponibilité de base de données. Ce concept est connu sous le nom de mobilité des bases de données.

Groupe – L’étendue de la disponibilité est déterminée par les serveurs de boîtes aux lettres d’un groupe de disponibilité de base de données, réunis au sein d’un cluster de basculement et fonctionnant conjointement sous forme de groupe.

Disponibilité – Ce terme semble le moins évident et le plus flou (alors qu’il est lié aux deux autres termes). Ironie de l’histoire, il a une définition mathématique simple et joue un rôle important dans la compréhension des principes globaux de conception d’Exchange.

Wikipédia définit la « disponibilité » comme suit :

Stade auquel se trouve un système, un sous-système ou un équipement dans le cadre d’un état opérationnel spécifique au début d’une mission, lorsque la mission est mise en œuvre à un moment inconnu, c’est-à-dire aléatoire. Autrement dit, la disponibilité est le ratio de temps pendant lequel un système se trouve en état de fonctionnement. On parle également de taux de disponibilité. Mathématiquement, cela s’exprime sous la forme 1 moins indisponibilité.
Division du (a) temps total pendant lequel une unité fonctionnelle est susceptible d’être utilisée pendant un intervalle donné par (b) la longueur de l’intervalle.

En théorie des probabilités, ces deux définitions signifient la même chose : probabilité qu’un système ou composant donné soit « opérationnel » ou « capable d’être utilisé » (en d’autres termes disponible) à tout moment (où il est testé).

En mathématiques, il est possible de mesurer cette notion en calculant la durée de disponibilité (« temps de fonctionnement ») pendant une période suffisamment significative d’un point de vue statistique (généralement une année), puis en la divisant par la durée totale de la période. À l’aide des acronymes MTBF (temps moyen entre les défaillances) et MTTR (temps moyen de réparation), le premier représente la disponibilité / le temps de fonctionnement entre les défaillances alors que le second représente le temps d’arrêt du système au cours d’une défaillance, il est possible d’exprimer la disponibilité sous forme de fraction :

La caractéristique mathématique opposée est une probabilité de défaillance (« indisponibilité ») :

La disponibilité est souvent exprimée en « nombre de chiffres neuf », comme le montre le tableau suivant :

Niveau de disponibilité	Valeur de disponibilité	Probabilité de défaillance	Temps d’arrêt accepté par année
Deux neuf	99 %	1 %	5 256 minutes = 3,65 jours
Trois neuf	99,9 %	0,1 %	525,6 minutes = 8,76 heures
Quatre neuf	99,99 %	0,01 %	52,56 minutes
Cinq neuf	99,999 %	0,001 %	5,26 minutes

Naturellement, la valeur de disponibilité diffère selon que l’on prend en compte le temps d’arrêt planifié (prévu) et non planifié (non prévu) ou seulement le temps d’arrêt non planifié. Le contrat SLA (Service Level Agreement) qui représente les exigences de disponibilité du point de vue de l’entreprise doit être très précis sur la question. Dans tous les cas, la disponibilité d’un système ou d’un composant donné dépend de nombreux facteurs. Par conséquent, il est très important d’identifier et de comprendre ces dépendances, ainsi que leur impact sur la disponibilité.

Impact des dépendances de service sur la disponibilité

La disponibilité d’une base de données de boîtes aux lettres Exchange dépend de la disponibilité de nombreux autres services et composants (par exemple le sous-système de stockage qui héberge la base de données, le serveur qui gère cette base de données, la connectivité réseau au serveur, etc.). Tous ces éléments sont des composants critiques, la défaillance d’un seul d’entre eux entraîne une perte de service, même si l’intégrité de la base de données elle-même est garantie. Cela signifie que pour que la base de données soit disponible en tant que service, chaque dépendance de la base de données doit être disponible également. Si nous identifions et isolons correctement les composants de dépendance, nous pouvons calculer mathématiquement la façon dont ils déterminent la disponibilité résultante de la base de données de boîtes aux lettres Exchange.

Pour une base de données de boîtes aux lettres Exchange donnée, les éléments suivants peuvent être considérés comme des dépendances critiques :

disque de base de données / sous-système de stockage – Disons que sa disponibilité est de niveau A₁ ;
serveur de boîtes aux lettres (composants matériels et logiciels) – Disons que sa disponibilité est de niveau A₂ ;
serveur d’accès au client (composants matériels et logiciels) – N’oubliez pas que dans Exchange 2010, tous les clients se connectent à une base de données de boîtes aux lettres uniquement via un serveur d’accès au client. En outre, supposons que le serveur d’accès au client est installé à l’écart du serveur de boîtes aux lettres dans le cas présent. Disons que sa disponibilité est de niveau A₃ ;
connectivité réseau entre les clients et le serveur d’accès au client, ainsi qu’entre le serveur d’accès au client et le serveur de boîtes aux lettres – Disons que sa disponibilité est de niveau A₄ ;
alimentation du centre de données où sont situés les serveurs et le stockage – Disons que sa disponibilité est de niveau A₅.

La liste est longue... Par exemple, Active Directory et DNS représentent également des dépendances critiques pour Exchange. Par ailleurs, outre les dépendances technologiques pures, la disponibilité est impactée par les dépendances de processus telles que la maturité opérationnelle, etc. : les erreurs humaines, les opérations définies de façon incorrecte, le manque de coordination au niveau de l’équipe peuvent entraîner des interruptions de service. Nous n’allons pas essayer de compiler une liste exhaustive des dépendances mais nous concentrer plutôt sur la façon dont elles affectent la disponibilité de l’ensemble du service.

Étant donné que ces composants sont indépendants les uns des autres, la disponibilité de chaque composant représente un événement indépendant. La disponibilité résultante d’une base de données de boîtes aux lettres Exchange représente une combinaison de tous ces événements (en d’autres termes, pour qu’une base de données de boîtes aux lettres soit disponible pour les clients, tous ces composants doivent être disponibles). En théorie des probabilités, la probabilité d’une combinaison d’événements indépendants est le produit des probabilités individuelles de chaque événement :

Par exemple, si vous jouez à pile ou face avec trois pièces, la probabilité d’obtenir le côté pile avec les trois pièces est de (1/2)*(1/2)*(1/2) = 1/8.

Il est important de comprendre que dans la mesure où chaque valeur de disponibilité ne peut pas être supérieure à 1 (ou 100 %) et que la disponibilité de service résultante est simplement un produit des disponibilités des composants individuels, la valeur de disponibilité résultante ne peut pas être supérieure à la valeur de disponibilité la plus faible des composants dépendants.

Cela peut être illustré par l’exemple présenté dans le tableau suivant (les nombres ici sont des échantillons suffisamment réalistes) :

Composant de dépendance critique	Probabilité de défaillance	Valeur de disponibilité
Serveur de boîtes aux lettres et stockage de boîtes aux lettres	5 %	95 %
Serveur d’accès au client	1 %	99 %
Réseau	0,5 %	99,5 %
Alimentation	0,1 %	99,9 %
Ensemble du service (dépend de tous les composants ci-dessus)	6,51383 %	95 % x 99 % x 99,5 % x 99,9 % = 93,48617 %

Cet exemple vous permet de voir à quel point les dépendances de service sont d’une importance capitale. Même pour une base de données de boîtes aux lettres qui ne rencontre aucune défaillance (aucune altération, aucune infection virale, etc.), la disponibilité reste encore inférieure à 93,5 %.

Conclusion : un grand nombre de dépendances de service fait baisser la disponibilité.

Tout ce que vous pouvez faire pour diminuer l’impact des dépendances de service a une conséquence positive en matière de disponibilité de l’ensemble du service. Par exemple, vous pouvez améliorer la maturité opérationnelle en simplifiant et en sécurisant la gestion des serveurs et en optimisant les procédures opérationnelles. Sur le plan technique, vous pouvez essayer de réduire le nombre des dépendances de service en simplifiant leur conception : par exemple, en éliminant les dispositifs de stockage SAN complexes, notamment les cartes HBA, les commutateurs à fibre, les contrôleurs de groupes et même les contrôleurs RAID afin de les remplacer par une solution DAS simple avec un minimum de changements de composants.

La réduction des dépendances de service peut s’avérer insuffisante pour atteindre le niveau souhaité de disponibilité. Il existe un autre moyen très efficace d’augmenter la disponibilité résultante et de minimiser l’impact des dépendances de service critiques : pour ce faire, il faut tirer parti des diverses méthodes de redondance telles que la duplication de l’alimentation, l’association de deux cartes réseau, la connexion des serveurs à plusieurs commutateurs réseau, l’utilisation d’une protection RAID pour le système d’exploitation, le déploiement de solutions d’équilibrage de charge pour les serveurs d’accès au client et de plusieurs copies de base de données de boîtes aux lettres. Mais comment la redondance peut-elle accroître la disponibilité ? Examinons de plus près des exemples significatifs en matière d’équilibrage de charge et de copies de base de données multiples.

Impact de la redondance sur la disponibilité

Du point de vue conceptuel, toutes les méthodes de redondance ont la même visée : plusieurs instances du composant sont disponibles et peuvent être utilisées soit conjointement avec d’autres instances (comme dans l’équilibrage de charge), soit en tant que solutions de substitution (comme dans les copies de base de données multiples). Supposons que nous ayons n instances d’un composant donné (n serveurs dans un groupe de serveurs d’accès au client ou n copies de base de données dans un groupe de disponibilité de base de données). Même en cas de défaillance de l’une des instances, les autres instances peuvent toujours être utilisées de manière à préserver la disponibilité. La défaillance de l’ensemble des instances est la seule situation où nous devons faire face à un temps d’arrêt effectif.

Tel que cela a été défini précédemment, la probabilité de défaillance d’une instance donnée est P = 1 – A. Toutes les instances sont statistiquement indépendantes les unes des autres, ce qui signifie que la disponibilité ou la défaillance de l’une d’entre elles n’affecte pas la disponibilité des autres instances. Par exemple, la défaillance d’une copie de base de données spécifique n’affecte pas la probabilité de défaillance d’une autre copie de cette base de données. Il convient de rappeler qu’une altération de la base de données logique peut néanmoins se propager de la première copie de base de données endommagée à l’ensemble des autres copies, mais ignorons ce facteur hautement improbable pour l’instant. Après tout, vous pouvez toujours mettre en œuvre une copie de base de données décalée ou une sauvegarde classique avec récupération jusqu’à une date et heure pour éluder cet aspect.

Une fois de plus, si nous utilisons le même théorème de la théorie des probabilités, la probabilité de défaillance d’un ensemble de n composants indépendants est le produit des probabilités de chaque composant. Comme tous les composants sont identiques ici (différentes instances du même objet), le produit devient une puissance :

Apparemment, comme P < 1, Pⁿ est inférieur à P, ce qui signifie que la probabilité de défaillance diminue, et qu’en conséquence la disponibilité augmente :

Prenons un exemple concret pour plus de clarté. Nous déployons plusieurs copies de base de données de boîtes aux lettres ; chaque copie est hébergée sur un lecteur SATA unique. Statistiquement, le taux de défaillance des lecteurs SATA est d’environ 5 % par an[1], ce qui nous donne une probabilité de défaillance de 5 % : P = 0,05 (ce qui signifie une disponibilité de 95 % : A = 0,95). Comment évolue la disponibilité lorsque nous ajoutons des copies de base de données supplémentaires ? Examinez le tableau suivant dont le contenu est explicite :

Nombre de copies de base de données	Probabilité de défaillance	Valeur de disponibilité
1	P₁ = P = 5 %	A₁ = 1 – P₁ = 95 %
2	P₂ = P² = 0,25 %	A₂ = 1 – P₂ = 99,75 %
3	P₃ = P³ = 0,0125 %	A₃ = 1 – P₃ = 99,9875 %
4	P₄ = P⁴ = 0,000625 %	A₄ = 1 – P₄ = 99,9994 %

Impressionnant, n’est-ce pas ? Concrètement, chaque copie de base de données supplémentaire sur le lecteur SATA introduit le facteur de multiplication de 5 % ou 1/20 ; par conséquent, la probabilité de défaillance devient 20 fois plus faible avec chaque copie (et, parallèlement, la disponibilité augmente). Vous pouvez constater que même avec la plupart des lecteurs SATA les moins fiables, le déploiement de 4 copies de base de données suffit à élever le niveau de disponibilité de la base de données à cinq neuf.

Bien que ce résultat soit très bon, pouvez-vous faire encore mieux ? Pouvez-vous augmenter davantage la disponibilité sans apporter de modifications à l’architecture (par exemple, dans l’hypothèse où l’ajout d’une nouvelle copie de base de données ne serait pas possible) ?

Absolument. Si vous améliorez la disponibilité individuelle d’un composant de dépendance, celui-ci devient un facteur d’augmentation de la disponibilité de l’ensemble du service et produit un impact beaucoup plus important que l’ajout de composants redondants. Par exemple, l’une des manières d’y parvenir sans se ruiner consiste à utiliser des lecteurs Nearline SAS au lieu de lecteurs SATA. Les lecteurs Nearline SAS ont un taux de défaillance annuel d’environ 2,75 % contre environ 5 % pour les lecteurs SATA. Cela réduit la probabilité de défaillance du composant de stockage dans le calcul ci-dessus et augmente, par conséquent, la disponibilité de l’ensemble du service. Il suffit de comparer cette observation à l’impact de l’ajout de plusieurs copies de base de données :

Taux de défaillance annuel de 5 % = facteur de multiplication de 1/20 = chaque nouvelle copie rend la défaillance de base de données 20 fois moins probable.
Taux de défaillance annuel de 2,75% = facteur de multiplication de 1/36 = chaque nouvelle copie rend la défaillance de base de données 36 fois moins probable.

Cet impact significatif des copies de base de données supplémentaires sur la disponibilité d’une base de données est également évoqué dans nos conseils en matière de protection des données natives Exchange (Exchange Native Data Protection). En effet, il est indiqué que plusieurs copies de base de données peuvent remplacer les sauvegardes traditionnelles si suffisamment de copies de base de données (trois ou plus) sont déployées.

La même logique s’applique au déploiement de plusieurs serveurs d’accès au client dans un groupe de serveurs d’accès au client, de plusieurs commutateurs réseau, etc. Par exemple, nous avons déployé 4 copies de base de données et 4 serveurs d’accès au client. Revenons à présent au tableau de disponibilité des composants analysé plus haut :

Composant de dépendance critique	Probabilité de défaillance	Valeur de disponibilité
Serveur de boîtes aux lettres et stockage de boîtes aux lettres (4 copies)	5 % ^ 4 = 0,000625 %	99,999375 %
Serveur d’accès au client (4 serveurs installés séparément)	1 % ^ 4 = 0,000001 %	99,999999 %
Réseau	0,5 %	99,5 %
Alimentation	0,1 %	99,9 %
Ensemble du service (dépend de tous les composants ci-dessus)	0,6 %	99,399878 %

Comme vous pouvez le constater, le simple fait de déployer 4 serveurs d’accès au client et 4 copies de base de données divise par 10 la probabilité de défaillance de l’ensemble du service (de 6,5 % à 0,6 %) et augmente, par conséquent, la disponibilité du service de 93,5 % à 99,4 %, ce qui représente une valeur plus qu’intéressante.

Conclusion : l’ajout d’une redondance aux dépendances de service augmente la disponibilité.

Réunion des éléments

Une question intéressante se pose à partir des conclusions précédentes. Nous avons analysé deux facteurs différents ayant deux types d’impacts sur la disponibilité de l’ensemble du service et nous sommes parvenus à deux conclusions claires :

L’ajout de dépendances système supplémentaires réduit la disponibilité.
L’ajout d’une redondance aux dépendances système augmente la disponibilité.

Que se passe-t-il si les deux situations sont des facteurs de solution ? Quelle tendance est la plus forte ?

Examinez le scénario suivant :

Nous déployons deux serveurs de boîtes aux lettres dans un groupe de disponibilité de base de données avec deux copies de base de données de boîtes aux lettres (une copie sur chaque serveur) et nous déployons deux serveurs d’accès au client dans un groupe à charge équilibrée. (Pour plus de simplicité, nous allons seulement examiner la disponibilité d’une base de données de boîte aux lettres pour des connexions clientes, en laissant de côté pour l’instant le transport Hub et la messagerie unifiée). En partant du principe que chaque serveur a une probabilité de défaillance individuelle P, la disponibilité d’un tel système est-elle meilleure ou moins bonne que la disponibilité d’un serveur Exchange autonome unique dont le rôle serveur de boîte aux lettres et le rôle serveur d’accès au client sont déployés ?

Dans le premier scénario, les serveurs de boîtes aux lettres sont indépendants. Ils ne sont indisponibles qu’en cas de défaillance des deux serveurs. La probabilité de défaillance de l’ensemble constitué des deux serveurs de boîtes aux lettres équivaut à : P × P = P². Par conséquent, sa disponibilité équivaut à : A_MBX = 1 – P². Selon la même logique, les services du serveur d’accès au client sont indisponibles uniquement en cas de défaillance des deux serveurs d’accès au client ; par conséquent, la probabilité de défaillance de l’ensemble constitué des deux serveurs d’accès au client équivaut à nouveau à : P × P = P² et, parallèlement, sa disponibilité équivaut à : A_CAS = 1 – P².

Dans le cas présent, comme vous l’aurez peut-être compris, deux serveurs de boîtes aux lettres ou deux serveurs d’accès au client sont des exemples de composants système redondants.

Toujours selon le même scénario... Pour permettre à la totalité du système d’être disponible, les deux ensembles de serveurs (ensemble constitué des serveurs de boîtes aux lettres et ensemble constitué des serveurs d’accès au client) doivent être disponibles simultanément. Ils ne doivent pas rencontrer de défaillance simultanément mais doivent être disponibles simultanément, car ils représentent désormais des dépendances système et non des composants redondants. Cela signifie que la disponibilité de la totalité du service est le produit des disponibilités de chaque ensemble :

Naturellement, le second scénario est bien plus commode, car il n’y a qu’un seul serveur à prendre en considération et sa disponibilité se traduit simplement par A = 1 – P.

Maintenant que nous avons calculé les valeurs de disponibilité des deux scénarios, quelle est la valeur la plus élevée (1-P²)² ou 1-P ?

Si nous traçons les graphiques des deux fonctions, nous constatons le comportement suivant :

(J’ai utilisé le moteur de calcul gratuit Wolfram Alpha Mathematica Online pour réaliser le tracé rapidement et facilement).

Nous pouvons voir que pour les valeurs faibles de P, la disponibilité du système complexe à 4 serveurs est supérieure à la disponibilité du serveur unique. Cela n’est pas surprenant, c’est ce que nous attendions, n’est-ce pas ? Toutefois, lorsque la valeur de P est égale à environ 0,618 (plus précisément, 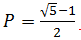) les deux tracés se croisent, et pour les valeurs plus importantes de P le système basé sur un serveur unique offre en fait une disponibilité plus importante. Naturellement, en situation réelle, vous souhaitez que la valeur de P soit très proche de zéro ; cependant, si vous envisagez de créer votre solution à partir de composants très incertains en matière de fiabilité, il est préférable de choisir un serveur unique.

Impact des domaines de défaillance

Malheureusement, dans la réalité, les scénarios de déploiement sont rarement aussi simples que les situations décrites ci-dessus. Par exemple, comment évolue la disponibilité du service si vous déployez des serveurs à rôles multiples ? Nous avons remarqué dans le scénario ci-dessus que la combinaison des rôles serveur permet de réduire efficacement le nombre de dépendances de service, ce qui est probablement une bonne chose, n’est-ce pas ? Que se passe-t-il si vous placez deux copies de la même base de données dans le même groupe SAN ou le même boîtier DAS ? Que se passe-t-il si tous vos serveurs de boîtes aux lettres sont connectés au même commutateur réseau ? Que se passe-t-il si votre situation correspond à tout ce qui a été évoqué précédemment et à bien d’autres choses encore ?

Toutes ces situations sont liées au concept des domaines de défaillance. Dans les exemples ci-dessus, le matériel serveur, le groupe SAN ou le commutateur réseau représentent un domaine de défaillance. Un domaine de défaillance rompt l’indépendance ou la redondance des composants qu’il combine (par exemple, la défaillance du matériel serveur dans un serveur à rôles multiples signifie que tous les rôles Exchange de ce serveur deviennent indisponibles) ; par conséquent, la défaillance d’un boîtier de disque ou d’un groupe SAN signifie que toutes les copies de base de données hébergées dans ce boîtier ou ce groupe deviennent indisponibles.

Les domaines de défaillance ne sont pas nécessairement une mauvaise chose. La différence importante réside dans les types de composants qui constituent un domaine de défaillance : s’agit-il de dépendances système distinctes ou de composants système redondants ? Prenons deux des exemples ci-dessus pour saisir cette différence.

Scénario de serveur à rôles multiples

Comparons la disponibilité de deux systèmes distincts :

deux rôles serveur (rôle serveur de boîte aux lettres et rôle serveur d’accès au client) hébergés sur le même serveur dont la probabilité de défaillance matérielle est P ;
rôles identiques hébergés sur deux serveurs distincts, chacun ayant la même probabilité de défaillance matérielle.

Dans le premier cas, le matériel d’un serveur unique représente un domaine de défaillance. Cela signifie que tous les rôles hébergés sont soit disponibles, soit indisponibles. C’est simple, la disponibilité globale d’un tel système se traduit par A = 1 – P.

Dans le second cas, l’ensemble du service n’est disponible que lorsque les deux serveurs sont disponibles de manière indépendante (car chaque rôle représente une dépendance critique). Par conséquent, d’après la théorie des probabilités, la disponibilité se traduit par A × A = A².

À nouveau, comme A < 1, cela signifie que A² < A ; par conséquent, dans le second cas, la disponibilité est plus faible.

Apparemment, nous pouvons ajouter d’autres rôles serveur Exchange (transport Hub et messagerie unifiée, si nécessaire) au même scénario sans briser cette logique.

Conclusion : la colocation des rôles serveur Exchange sur un serveur à rôles multiples augmente la disponibilité de l’ensemble du service.

Scénario de stockage partagé

Considérons à présent un autre scénario de domaine de défaillance (deux copies de base de données partageant le même groupe de stockage) et comparons la disponibilité de la base de données dans les deux cas suivants :

deux copies de base de données hébergées dans le même espace de stockage partagé (groupe SAN ou boîtier DAS), dont la probabilité de défaillance est P ;
copies de base de données identiques hébergées sur deux systèmes de stockage distincts, chacun ayant la même probabilité de défaillance.

Dans le premier cas, le stockage partagé représente un domaine de défaillance. Comme dans le scénario précédent, cela signifie que les deux copies de base de données sont disponibles ou indisponibles simultanément ; par conséquent, la disponibilité globale se traduit à nouveau par A = 1 – P.

Dans le second cas, l’ensemble du service est disponible si au moins un système est disponible et est indisponible uniquement en cas de défaillance des deux systèmes. Les systèmes de stockage en question sont indépendants ; par conséquent, la probabilité de défaillance de l’ensemble du service équivaut à P × P = P² et la disponibilité correspondante de l’ensemble du service équivaut à A = 1 – P².

À nouveau, comme P < 1, cela signifie que P² < P et par conséquent que 1 – P² > 1 – P. En d’autres termes, la disponibilité est plus élevée dans le second cas.

Conclusion : la colocation de copies de base de données sur le même système de stockage réduit la disponibilité de l’ensemble du service.

Quelle est la différence entre ces deux scénarios ? Pourquoi est-ce que l’introduction d’un domaine de défaillance augmente la disponibilité dans le premier cas et réduit la disponibilité dans le second ?

Cela est dû au fait que dans le premier cas, le domaine de défaillance combine des dépendances de service, ce qui réduit leur nombre de manière effective et améliore par conséquent la disponibilité, alors que dans le second cas, le domaine de défaillance combine des composants redondants, ce qui réduit la redondance de manière effective et compromet par conséquent la disponibilité.

Il est possible de visualiser l’ensemble de ces concepts et conclusions comme suit :

(Non, nous n’avons pas utilisé Wolfram Alpha pour dessiner ce graphique.)

Résumé

L’architecture d’Exchange 2010 offre de puissantes possibilités pour ajouter de la redondance au niveau d’Exchange (par exemple en déployant plusieurs copies de base de données ou plusieurs serveurs d’accès au client dans un groupe de serveurs d’accès au client) et réduire le nombre de dépendances système (en combinant les rôles serveur Exchange dans un serveur à rôles multiples ou en utilisant une architecture de stockage plus simple sans excès de composants critiques). Les règles et formules simples présentées dans cet article vous permettent de calculer l’effet de la valeur de disponibilité à partir du déploiement de copies de base de données supplémentaires ou de la combinaison de rôles serveur Exchange ; vous pouvez également calculer l’impact des domaines de défaillance. Il est important de noter que nous avons essayé d’utiliser ces modèles mathématiques simples pour illustrer les concepts, et non pour prétendre obtenir des valeurs de disponibilité précises. La réalité correspond rarement à la simplicité des scénarios de base, vous devez effectuer bien plus de calculs complexes pour obtenir des estimations raisonnables de la disponibilité de vos systèmes réels ; il peut s’avérer plus facile de mesurer simplement la disponibilité de manière statistique et de vérifier si elle répond aux exigences du contrat SLA. Toutefois, la compréhension des facteurs qui affectent la disponibilité et la conscience de leur interaction dans une solution d’ingénierie complexe doivent vous permettre de concevoir cette solution de manière appropriée et d’atteindre une augmentation significative de la disponibilité de l’ensemble du service afin de répondre aux exigences professionnelles les plus avancées.

Boris Lokhvitsky
Architecte informatique

[1] Les études suivantes menées par l’Université Carnegie Mellon, Google et Microsoft Research montrent un taux de défaillance annuel de 5 % pour les lecteurs SATA :

https://www.usenix.org/events/fast07/tech/schroeder/schroeder.pdf

https://labs.google.com/papers/disk_failures.pdf

https://research.microsoft.com/research/pubs/view.aspx?msr_tr_id=MSR-TR-2005-166