Déterminer la combinaison optimale de chevauchement de remises
Cet article explique comment déterminer la combinaison optimale de remises qui se chevauchent dans Microsoft Dynamics 365 Commerce.
Lorsque les remises se chevauchent, vous devez déterminer la combinaison de chevauchement des remises qui produit le plus petit total de transaction ou la remise totale la plus élevée. Lorsque le montant de la remise varie en fonction du prix des produits achetés, comme dans le cas de la remise sur la vente au détail commune « Acheter 1, obtenir 1 X pour cent de remise » (BOGO), ce processus devient un problème d’optimisation combinatoire.
Cet article s’applique à Microsoft Dynamics AX 2012 R3 avec la Base de connaissances 3105973 (publiée le 2 novembre 2015) ou ultérieure, et Dynamics 365 Commerce. Pour déterminer la combinaison chevauchant les remises à appliquer en temps voulu, nous avons introduit une méthode pour appliquer des remises se chevauchant Nous appelons cette nouvelle méthode classement de valeur marginale. Dans la méthode de classement de valeur marginale, une valeur est calculée pour chaque remise se chevauchant à l’aide de la valeur de la remise sur les produits partagés. Les remises chevauchées sont ensuite appliquées de la valeur relative la plus élevée à la valeur relative la plus faible. Pour plus d’informations sur la nouvelle méthode, voir la section Méthode de classement de la valeur marginale, plus loin dans cet article. Le classement de valeur marginale n’est pas utilisé lorsque les montants de remise pour un produit ne sont pas affectés par un autre produit dans la transaction. Par exemple, cette méthode n’est pas utilisée pour deux remises simples, ou pour une remise simple et une remise unique de la quantité de produits.
Exemples de remise
Vous pouvez créer un nombre illimité de remises sur un ensemble courant de produits. Toutefois, car il n’y a aucune limite, les problèmes de performances peuvent survenir lorsque vous essayez de calculer les remises qui doivent être utilisées sur les différents produits. Les exemples suivants illustrent ce problème plus en détail. Dans l’exemple 1, nous commençons par deux produits et deux remises se chevauchant. Puis, dans l’exemple 2, nous indiquons la manière dont le problème évolue au fur et à mesure que des produits sont ajoutés.
Exemple 1 : Deux produits et deux remises
Dans cet exemple, deux produits sont nécessaires afin de pouvoir bénéficier de chaque remise, et les remises ne peuvent pas être combinées. Les remises dans cet exemple sont des remises Meilleur prix. Les deux produits qualifiés pour les deux remises. Voici les deux remises.

Pour deux produits, la meilleure de ces deux remises dépend des prix des deux produits. Lorsque le prix des deux produits est égal ou quasiment identiques, la remise 1 est préférable. Lorsque le prix d’un produit est considérablement inférieur au prix de l’autre produit, la remise 2 est préférable. Voici la règle mathématique pour évaluer ces deux remises, l’une en fonction de l’autre.
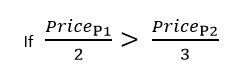
Note
Lorsque le prix du produit 1 est égal à deux-tiers du prix du produit 2, les deux remises sont égales. Dans cet exemple, le pourcentage de remise effective pour la remise 1 varie d’un faible pourcentage (lorsque les prix des deux produits sont distants) à un maximum de 25 % (lorsque les deux produits ont le même prix). Le pourcentage de remise effective pour la remise 2 est fixe. Elle est toujours de 20 %. Comme le pourcentage de remise effective pour la remise 1 a une plage qui peut être supérieure ou inférieure à la remise 2, la meilleure remise dépendra des prix des deux produits qui doivent être remisés. Dans cet exemple, le calcul est réalisé rapidement, car seules deux remises sont appliquées sur uniquement deux produits. Il existe uniquement deux combinaisons possibles : une application de la remise 1 ou une application de la remise 2. Il n’existe aucune permutation à calculer. La valeur de chaque remise est calculée à l’aide des deux produits, et la meilleure remise est utilisée.
Exemple 2 : Quatre produits et deux remises
Ensuite, nous utiliserons quatre produits et les deux mêmes remises. Les quatre produits qualifiés pour les deux remises. Il existe douze combinaisons possibles. En fin de compte, deux réductions seront appliquées à la transaction dans l’une des trois combinaisons : deux applications de réduction 1, deux applications de réduction 2 ou une application de réduction 1 et une application de réduction 2. Pour illustrer les combinaisons possibles, nous regarderons deux ensembles différents de quatre produits avec des prix différents :
- Les quatre produits ont le même prix de $15. Dans ce cas, la meilleure combinaison de remises est deux applications de la remise 1. Deux produits seront à plein tarif et deux bénéficieront d’une remise de 50 %. Le total remisé de la transaction est $45 (15 + 15 + 7,50 + 7,50), qui est $15 (25 %) déduit du total non remisé de $60. La remise 2 n’est que de $12 (20 %).
- Deux produits sont à $20 chacun, un produit est à $15 et un autre produit est à $5. Dans ce cas, la meilleure combinaison de remise est une application de la remise 2 et une application de la remise 1. Les tableaux ci-dessous illustrent les remises.
Pour lire les tableaux, utilisez un produit d’une ligne et un produit d’une colonne. Par exemple, dans le tableau pour la remise 1, lorsque vous combinez les deux produits à $20, vous obtenez une remise de $10. Dans le tableau pour la remise 2, lorsque vous combinez le produit de $15 et le produit de $5, vous obtenez une remise de $4.
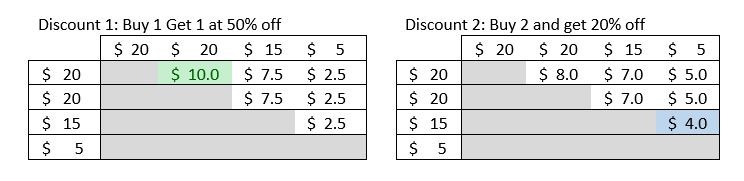
En premier, nous trouvons la plus grande remise qui est disponible à partir de deux produits à l’aide de l’une ou l’autre des remises. Les deux tableaux montrent la quantité de remise pour toutes les combinaisons des deux produits. Les parties ombrées des tableaux représentent soit les cas où un produit est associé à lui-même, ce que nous ne pouvons pas faire, soit un couplage en sens inverse de deux produits qui produit le même montant de remise et peut être ignoré. En examinant les tableaux, vous pouvez voir que la remise 1 pour les deux articles à $20 est la plus grande remise disponible pour l’une ou l’autre des remises sur chacun des quatre produits. (Cette remise est mise en surbrillance en vert dans le premier tableau.) Cela laisse uniquement le produit à $15 et le produit à $5. En examinant les deux tableaux de nouveau, vous pouvez voir que, pour ces deux produits, la remise 1 donne une remise de $2,50, alors que la remise 2 donne une remise de $4. Par conséquent, nous sélectionnons la remise 2. La remise totale est de $14. Pour faciliter la visualisation de cette discussion, voici deux tableaux supplémentaires qui affichent le pourcentage de remise effective pour toutes les combinaisons possibles pour les remise 1 et remise 2. Seule la moitié de la liste des combinaisons est incluse, car, pour ces deux remises, l’ordre dans lequel les deux produits sont ajoutés dans la remise n’importe pas. La remise effective la plus élevée (25 %) est mise en surbrillance en vert, et la plus faible remise effective (10 %) est mise en surbrillance en rouge.
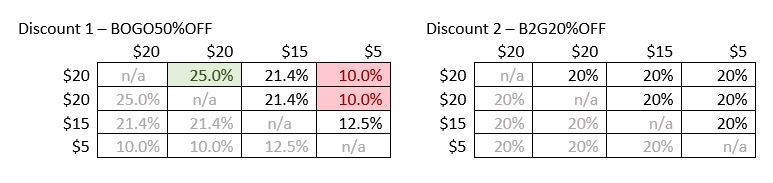
Note
Lorsque les prix varient, et qu’au moins deux remises se concurrencent, la seule façon de garantir la meilleure combinaison de remises est d’évaluer les deux remises et de les comparer.
Combinaisons possibles totales
Cette section continue l’exemple de la section précédente. Nous ajouterons plus de produits et une remise différente, puis nous verrons le nombre de combinaisons devant être calculées et comparées. Le tableau suivant indique le nombre de combinaisons de remises possibles au fur et à mesure que la quantité de produits augmente. Le tableau montre ce qui se produit à la fois lorsqu’il y a deux remises se chevauchant, comme dans l’exemple précédent, et lorsqu’il y a trois remises se chevauchant. Le nombre de combinaisons de rabais possibles qui doivent être évaluées dépasse rapidement ce que même un ordinateur rapide peut calculer et comparer assez rapidement pour être acceptable pour les transactions de détail.
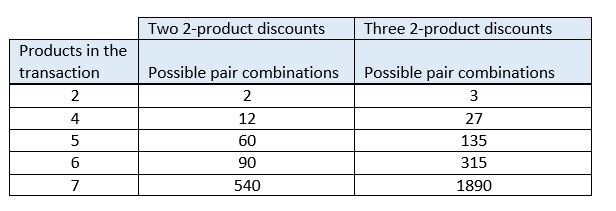
Lorsque des quantités encore plus importantes ou plus de remises se chevauchant sont appliquées, le nombre total de combinaisons de remises possibles se traduit rapidement en millions, et le temps requis pour évaluer et sélectionner la meilleure combinaison possible devient rapidement perceptible. Certaines optimisations ont été effectuées dans le moteur de prix afin de réduire le nombre total de combinaisons à évaluer. Toutefois, comme le nombre de remises se chevauchant et les quantités dans une transaction ne sont pas limitées, un grand nombre de combinaisons doivent toujours être évaluées dès qu’il y a des remises qui se chevauchent. Ce problème est le problème auquel la méthode de classement de valeur marginale s’adresse.
Méthode de classement de la valeur marginale
Pour résoudre le problème d’un nombre exponentiel de combinaisons qui doivent être évaluées, il existe une optimisation qui calcule la valeur par produit partagé de chaque remise sur l’ensemble des produits auxquels on peut appliquer deux remises ou plus. Nous nous référons à cette valeur comme valeur marginale de la remise pour les produits partagés. La valeur marginale est la moyenne par augmentation de produit dans le montant de remise totale lorsque les produits partagés sont inclus dans chaque remise. La valeur marginale est calculée en prenant le montant de remise totale (DTotal), soustrayant le montant de remise sans produits partagés (DMinus Shared), et divisant cette différence par le nombre de produits partagés (ItemsShared).
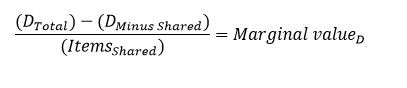
Après calcul de la valeur marginale de chaque remise sur un ensemble de produits partagés, les réductions s’appliquent aux produits partagés dans l’ordre, de manière exhaustive, de la valeur marginale la plus élevée à la valeur marginale la plus faible. Pour cette méthode, toutes les possibilités restantes de remise ne sont pas comparées à chaque fois qu’une seule instance d’une remise est appliquée. Au lieu de cela, les remises se chevauchant sont comparées une fois et ensuite appliquées dans l’ordre. Aucune comparaison supplémentaire n’est effectuée. Le calcul du classement par valeur marginale est déclenché automatiquement lorsque le nombre total de combinaisons possibles dépasse un seuil prédéfini. La durée acceptable pour calculer la remise totale varie entre différents secteurs au détail. Toutefois, la durée correspondante est en général une plage comprise entre des dizaines de millisecondes et une seconde.