Path Information and Enumeration
Get information about paths and enumerate the contents
The SKPath class defines several properties and methods that allow you to obtain information about the path. The Bounds and TightBounds properties (and related methods) obtain the metrical dimensions of a path. The Contains method lets you determine if a particular point is within a path.
It is sometimes useful to determine the total length of all the lines and curves that make up a path. Calculating this length is not an algorithmically simple task, so an entire class named PathMeasure is devoted to it.
It is also sometimes useful to obtain all the drawing operations and points that make up a path. At first, this facility might seem unnecessary: If your program has created the path, the program already knows the contents. However, you've seen that paths can also be created by path effects and by converting text strings into paths. You can also obtain all the drawing operations and points that make up these paths. One possibility is to apply an algorithmic transform to all the points, for example, to wrap text around a hemisphere:

Getting the Path Length
In the article Paths and Text you saw how to use the DrawTextOnPath method to draw a text string whose baseline follows the course of a path. But what if you want to size the text so that it fits the path precisely? Drawing text around a circle is easy because the circumference of a circle is simple to calculate. But the circumference of an ellipse or the length of a Bézier curve is not so simple.
The SKPathMeasure class can help. The constructor accepts an SKPath argument, and the Length property reveals its length.
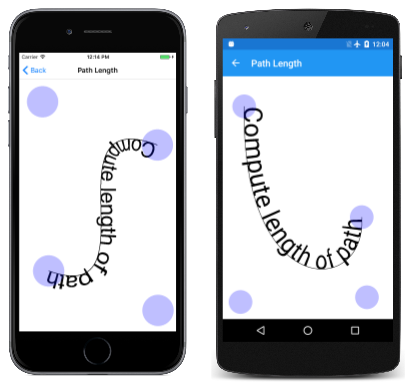
This class is demonstrated in the Path Length sample, which is based on the Bezier Curve page. The PathLengthPage.xaml file derives from InteractivePage and includes a touch interface:
<local:InteractivePage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:local="clr-namespace:SkiaSharpFormsDemos"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
xmlns:tt="clr-namespace:TouchTracking"
x:Class="SkiaSharpFormsDemos.Curves.PathLengthPage"
Title="Path Length">
<Grid BackgroundColor="White">
<skia:SKCanvasView x:Name="canvasView"
PaintSurface="OnCanvasViewPaintSurface" />
<Grid.Effects>
<tt:TouchEffect Capture="True"
TouchAction="OnTouchEffectAction" />
</Grid.Effects>
</Grid>
</local:InteractivePage>
The PathLengthPage.xaml.cs code-behind file allows you to move four touch points to define the end points and control points of a cubic Bézier curve. Three fields define a text string, an SKPaint object, and a calculated width of the text:
public partial class PathLengthPage : InteractivePage
{
const string text = "Compute length of path";
static SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Fill,
Color = SKColors.Black,
TextSize = 10,
};
static readonly float baseTextWidth = textPaint.MeasureText(text);
...
}
The baseTextWidth field is the width of the text based on a TextSize setting of 10.
The PaintSurface handler draws the Bézier curve and then sizes the text to fit along its full length:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with cubic Bezier curve
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.CubicTo(touchPoints[1].Center,
touchPoints[2].Center,
touchPoints[3].Center);
canvas.DrawPath(path, strokePaint);
// Get path length
SKPathMeasure pathMeasure = new SKPathMeasure(path, false, 1);
// Find new text size
textPaint.TextSize = pathMeasure.Length / baseTextWidth * 10;
// Draw text on path
canvas.DrawTextOnPath(text, path, 0, 0, textPaint);
}
...
}
The Length property of the newly created SKPathMeasure object obtains the length of the path. The path length is divided by the baseTextWidth value (which is the width of the text based on a text size of 10) and then multiplied by the base text size of 10. The result is a new text size for displaying the text along that path:
As the Bézier curve gets longer or shorter, you can see the text size change.
Traversing the Path
SKPathMeasure can do more than just measure the length of the path. For any value between zero and the path length, an SKPathMeasure object can obtain the position on the path, and the tangent to the path curve at that point. The tangent is available as a vector in the form of an SKPoint object, or as a rotation encapsulated in an SKMatrix object. Here are the methods of SKPathMeasure that obtain this information in varied and flexible ways:
Boolean GetPosition (Single distance, out SKPoint position)
Boolean GetTangent (Single distance, out SKPoint tangent)
Boolean GetPositionAndTangent (Single distance, out SKPoint position, out SKPoint tangent)
Boolean GetMatrix (Single distance, out SKMatrix matrix, SKPathMeasureMatrixFlags flag)
The members of the SKPathMeasureMatrixFlags enumeration are:
GetPositionGetTangentGetPositionAndTangent
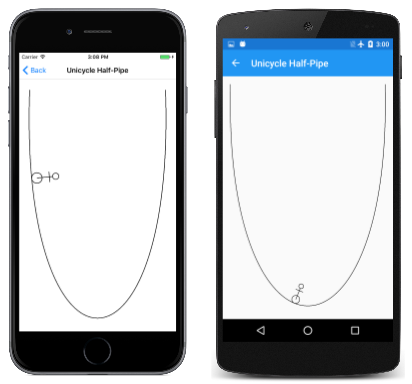
The Unicycle Half-Pipe page animates a stick figure on a unicycle that seems to ride back and forth along a cubic Bézier curve:
The SKPaint object used for stroking both the half-pipe and the unicycle is defined as a field in the UnicycleHalfPipePage class. Also defined is the SKPath object for the unicycle:
public class UnicycleHalfPipePage : ContentPage
{
...
SKPaint strokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
StrokeWidth = 3,
Color = SKColors.Black
};
SKPath unicyclePath = SKPath.ParseSvgPathData(
"M 0 0" +
"A 25 25 0 0 0 0 -50" +
"A 25 25 0 0 0 0 0 Z" +
"M 0 -25 L 0 -100" +
"A 15 15 0 0 0 0 -130" +
"A 15 15 0 0 0 0 -100 Z" +
"M -25 -85 L 25 -85");
...
}
The class contains the standard overrides of the OnAppearing and OnDisappearing methods for animation. The PaintSurface handler creates the path for the half-pipe and then draws it. An SKPathMeasure object is then created based on this path:
public class UnicycleHalfPipePage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPath pipePath = new SKPath())
{
pipePath.MoveTo(50, 50);
pipePath.CubicTo(0, 1.25f * info.Height,
info.Width - 0, 1.25f * info.Height,
info.Width - 50, 50);
canvas.DrawPath(pipePath, strokePaint);
using (SKPathMeasure pathMeasure = new SKPathMeasure(pipePath))
{
float length = pathMeasure.Length;
// Animate t from 0 to 1 every three seconds
TimeSpan timeSpan = new TimeSpan(DateTime.Now.Ticks);
float t = (float)(timeSpan.TotalSeconds % 5 / 5);
// t from 0 to 1 to 0 but slower at beginning and end
t = (float)((1 - Math.Cos(t * 2 * Math.PI)) / 2);
SKMatrix matrix;
pathMeasure.GetMatrix(t * length, out matrix,
SKPathMeasureMatrixFlags.GetPositionAndTangent);
canvas.SetMatrix(matrix);
canvas.DrawPath(unicyclePath, strokePaint);
}
}
}
}
The PaintSurface handler calculates a value of t that goes from 0 to 1 every five seconds. It then uses the Math.Cos function to convert that to a value of t that ranges from 0 to 1 and back to 0, where 0 corresponds to the unicycle at the beginning on the top left, while 1 corresponds to the unicycle at the top right. The cosine function causes the speed to be slowest at the top of the pipe and fastest at the bottom.
Notice that this value of t must be multiplied by the path length for the first argument to GetMatrix. The matrix is then applied to the SKCanvas object for drawing the unicycle path.
Enumerating the Path
Two embedded classes of SKPath allow you to enumerate the contents of path. These classes are SKPath.Iterator and SKPath.RawIterator. The two classes are very similar, but SKPath.Iterator can eliminate elements in the path with a zero length, or close to a zero length. The RawIterator is used in the example below.
You can obtain an object of type SKPath.RawIterator by calling the CreateRawIterator method of SKPath. Enumerating through the path is accomplished by repeatedly calling the Next method. Pass to it an array of four SKPoint values:
SKPoint[] points = new SKPoint[4];
...
SKPathVerb pathVerb = rawIterator.Next(points);
The Next method returns a member of the SKPathVerb enumeration type. These values indicate the particular drawing command in the path. The number of valid points inserted in the array depends on this verb:
Movewith a single pointLinewith two pointsCubicwith four pointsQuadwith three pointsConicwith three points (and also call theConicWeightmethod for the weight)Closewith one pointDone
The Done verb indicates that the path enumeration is complete.
Notice that there are no Arc verbs. This indicates that all arcs are converted into Bézier curves when added to the path.
Some of the information in the SKPoint array is redundant. For example, if a Move verb is followed by a Line verb, then the first of the two points that accompany the Line is the same as the Move point. In practice, this redundancy is very helpful. When you get a Cubic verb, it is accompanied by all four points that define the cubic Bézier curve. You don't need to retain the current position established by the previous verb.
The problematic verb, however, is Close. This command draws a straight line from the current position to the beginning of the contour established earlier by the Move command. Ideally, the Close verb should provide these two points rather than just one point. What's worse is that the point accompanying the Close verb is always (0, 0). When you enumerate through a path, you'll probably need to retain the Move point and the current position.
Enumerating, Flattening, and Malforming
It is sometimes desirable to apply an algorithmic transform to a path to malform it in some way:

Most of these letters consist of straight lines, yet these straight lines have apparently been twisted into curves. How is this possible?
The key is that the original straight lines are broken into a series of smaller straight lines. These individual smaller straight lines can then be manipulated in different ways to form a curve.
To help with this process, the sample contains a static PathExtensions class with an Interpolate method that breaks down a straight line into numerous short lines that are only one unit in length. In addition, the class contains several methods that convert the three types of Bézier curves into a series of tiny straight lines that approximate the curve. (The parametric formulas were presented in the article Three Types of Bézier Curves.) This process is called flattening the curve:
static class PathExtensions
{
...
static SKPoint[] Interpolate(SKPoint pt0, SKPoint pt1)
{
int count = (int)Math.Max(1, Length(pt0, pt1));
SKPoint[] points = new SKPoint[count];
for (int i = 0; i < count; i++)
{
float t = (i + 1f) / count;
float x = (1 - t) * pt0.X + t * pt1.X;
float y = (1 - t) * pt0.Y + t * pt1.Y;
points[i] = new SKPoint(x, y);
}
return points;
}
static SKPoint[] FlattenCubic(SKPoint pt0, SKPoint pt1, SKPoint pt2, SKPoint pt3)
{
int count = (int)Math.Max(1, Length(pt0, pt1) + Length(pt1, pt2) + Length(pt2, pt3));
SKPoint[] points = new SKPoint[count];
for (int i = 0; i < count; i++)
{
float t = (i + 1f) / count;
float x = (1 - t) * (1 - t) * (1 - t) * pt0.X +
3 * t * (1 - t) * (1 - t) * pt1.X +
3 * t * t * (1 - t) * pt2.X +
t * t * t * pt3.X;
float y = (1 - t) * (1 - t) * (1 - t) * pt0.Y +
3 * t * (1 - t) * (1 - t) * pt1.Y +
3 * t * t * (1 - t) * pt2.Y +
t * t * t * pt3.Y;
points[i] = new SKPoint(x, y);
}
return points;
}
static SKPoint[] FlattenQuadratic(SKPoint pt0, SKPoint pt1, SKPoint pt2)
{
int count = (int)Math.Max(1, Length(pt0, pt1) + Length(pt1, pt2));
SKPoint[] points = new SKPoint[count];
for (int i = 0; i < count; i++)
{
float t = (i + 1f) / count;
float x = (1 - t) * (1 - t) * pt0.X + 2 * t * (1 - t) * pt1.X + t * t * pt2.X;
float y = (1 - t) * (1 - t) * pt0.Y + 2 * t * (1 - t) * pt1.Y + t * t * pt2.Y;
points[i] = new SKPoint(x, y);
}
return points;
}
static SKPoint[] FlattenConic(SKPoint pt0, SKPoint pt1, SKPoint pt2, float weight)
{
int count = (int)Math.Max(1, Length(pt0, pt1) + Length(pt1, pt2));
SKPoint[] points = new SKPoint[count];
for (int i = 0; i < count; i++)
{
float t = (i + 1f) / count;
float denominator = (1 - t) * (1 - t) + 2 * weight * t * (1 - t) + t * t;
float x = (1 - t) * (1 - t) * pt0.X + 2 * weight * t * (1 - t) * pt1.X + t * t * pt2.X;
float y = (1 - t) * (1 - t) * pt0.Y + 2 * weight * t * (1 - t) * pt1.Y + t * t * pt2.Y;
x /= denominator;
y /= denominator;
points[i] = new SKPoint(x, y);
}
return points;
}
static double Length(SKPoint pt0, SKPoint pt1)
{
return Math.Sqrt(Math.Pow(pt1.X - pt0.X, 2) + Math.Pow(pt1.Y - pt0.Y, 2));
}
}
All these methods are referenced from the extension method CloneWithTransform also included in this class and shown below. This method clones a path by enumerating the path commands and constructing a new path based on the data. However, the new path consists only of MoveTo and LineTo calls. All the curves and straight lines are reduced to a series of tiny lines.
When calling CloneWithTransform, you pass to the method a Func<SKPoint, SKPoint>, which is a function with an SKPaint parameter that returns an SKPoint value. This function is called for every point to apply a custom algorithmic transform:
static class PathExtensions
{
public static SKPath CloneWithTransform(this SKPath pathIn, Func<SKPoint, SKPoint> transform)
{
SKPath pathOut = new SKPath();
using (SKPath.RawIterator iterator = pathIn.CreateRawIterator())
{
SKPoint[] points = new SKPoint[4];
SKPathVerb pathVerb = SKPathVerb.Move;
SKPoint firstPoint = new SKPoint();
SKPoint lastPoint = new SKPoint();
while ((pathVerb = iterator.Next(points)) != SKPathVerb.Done)
{
switch (pathVerb)
{
case SKPathVerb.Move:
pathOut.MoveTo(transform(points[0]));
firstPoint = lastPoint = points[0];
break;
case SKPathVerb.Line:
SKPoint[] linePoints = Interpolate(points[0], points[1]);
foreach (SKPoint pt in linePoints)
{
pathOut.LineTo(transform(pt));
}
lastPoint = points[1];
break;
case SKPathVerb.Cubic:
SKPoint[] cubicPoints = FlattenCubic(points[0], points[1], points[2], points[3]);
foreach (SKPoint pt in cubicPoints)
{
pathOut.LineTo(transform(pt));
}
lastPoint = points[3];
break;
case SKPathVerb.Quad:
SKPoint[] quadPoints = FlattenQuadratic(points[0], points[1], points[2]);
foreach (SKPoint pt in quadPoints)
{
pathOut.LineTo(transform(pt));
}
lastPoint = points[2];
break;
case SKPathVerb.Conic:
SKPoint[] conicPoints = FlattenConic(points[0], points[1], points[2], iterator.ConicWeight());
foreach (SKPoint pt in conicPoints)
{
pathOut.LineTo(transform(pt));
}
lastPoint = points[2];
break;
case SKPathVerb.Close:
SKPoint[] closePoints = Interpolate(lastPoint, firstPoint);
foreach (SKPoint pt in closePoints)
{
pathOut.LineTo(transform(pt));
}
firstPoint = lastPoint = new SKPoint(0, 0);
pathOut.Close();
break;
}
}
}
return pathOut;
}
...
}
Because the cloned path is reduced to tiny straight lines, the transform function has the capability of converting straight lines to curves.
Notice that the method retains the first point of each contour in the variable called firstPoint and the current position after each drawing command in the variable lastPoint. These variables are necessary to construct the final closing line when a Close verb is encountered.
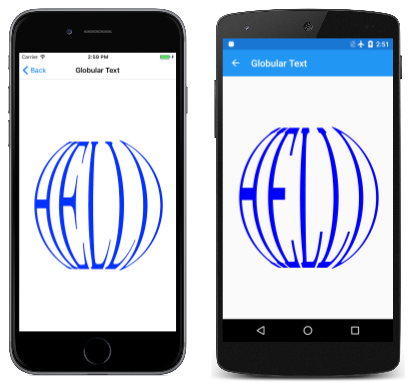
The GlobularText sample uses this extension method to seemingly wrap text around a hemisphere in a 3D effect:
The GlobularTextPage class constructor performs this transform. It creates an SKPaint object for the text, and then obtains an SKPath object from the GetTextPath method. This is the path passed to the CloneWithTransform extension method along with a transform function:
public class GlobularTextPage : ContentPage
{
SKPath globePath;
public GlobularTextPage()
{
Title = "Globular Text";
SKCanvasView canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
using (SKPaint textPaint = new SKPaint())
{
textPaint.Typeface = SKTypeface.FromFamilyName("Times New Roman");
textPaint.TextSize = 100;
using (SKPath textPath = textPaint.GetTextPath("HELLO", 0, 0))
{
SKRect textPathBounds;
textPath.GetBounds(out textPathBounds);
globePath = textPath.CloneWithTransform((SKPoint pt) =>
{
double longitude = (Math.PI / textPathBounds.Width) *
(pt.X - textPathBounds.Left) - Math.PI / 2;
double latitude = (Math.PI / textPathBounds.Height) *
(pt.Y - textPathBounds.Top) - Math.PI / 2;
longitude *= 0.75;
latitude *= 0.75;
float x = (float)(Math.Cos(latitude) * Math.Sin(longitude));
float y = (float)Math.Sin(latitude);
return new SKPoint(x, y);
});
}
}
}
...
}
The transform function first calculates two values named longitude and latitude that range from –π/2 at the top and left of the text, to π/2 at the right and bottom of the text. The range of these values isn't visually satisfactory, so they are reduced by multiplying by 0.75. (Try the code without those adjustments. The text becomes too obscure at the north and south poles, and too thin at the sides.) These three-dimensional spherical coordinates are converted to two-dimensional x and y coordinates by standard formulas.
The new path is stored as a field. The PaintSurface handler then merely needs to center and scale the path to display it on the screen:
public class GlobularTextPage : ContentPage
{
SKPath globePath;
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPaint pathPaint = new SKPaint())
{
pathPaint.Style = SKPaintStyle.Fill;
pathPaint.Color = SKColors.Blue;
pathPaint.StrokeWidth = 3;
pathPaint.IsAntialias = true;
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(0.45f * Math.Min(info.Width, info.Height)); // radius
canvas.DrawPath(globePath, pathPaint);
}
}
}
This is a very versatile technique. If the array of path effects described in the Path Effects article doesn't quite encompass something you felt should be included, this is a way to fill in the gaps.