Big Learning Made Easy – with Counts!
This post is by Misha Bilenko, Principal Researcher in Microsoft Azure Machine Learning.
This week, Azure ML is launching exciting new capability for training on terabytes of data. It is based on a surprisingly simple yet amazingly robust learning algorithm that is widely used by practitioners, yet receives virtually no dedicated attention in ML literature or courses. At the same time, the algorithm has been mentioned in passing in numerous papers across many fields, dating back to literature on branch prediction in compilers from early 1990s. It is also the workhorse for several multi-billion-dollar applications of ML, such as online advertising and fraud detection. Known under different names – ‘historical statistics’, ‘risk tables’, ‘CTR features’ – it retains the same core technique under the covers of different applications. In this blog post, we introduce the general form of this learning with counts method (which we call ‘Dracula’– to avoid saying “Distributed Robust Algorithm for Count-based Learning” each time, and to honor this children’s classic). We illustrate its use in Azure ML, where it allows learning to scale to terabytes of data with just a few clicks, and summarize the aspects that make it a great choice for practitioners.
In many prediction problems, the most informative data attributes are identities of objects, as they can be directly associated with the historical statistics collected for each object. For example, in click probability prediction for online advertising, key objects are the anonymous user, the ad, and the context (e.g., a query or a webpage). Their identities may be captured by such attributes as the user’s anonymous ID, a machine’s IP, an identifier for the ad or advertiser, and the text or hash for the query or webpage URL.
Identity attributes, as well as their combinations, hold enormous predictive power: e.g. given a user’s historical propensity to react to ads, the likelihood that a given ad is clicked for a particular query, the tendency to click on a certain advertiser’s ads from a particular location etc. While attribute values can be encoded as one-of-many (also known as one-hot) binary features, this results in very high-dimensional representation, which, when training with terabytes of data, practically limits one to use linear models. Although using attribute combinations can mitigate the paucity of linear representation, the resulting high-dimensional parameters remain difficult to interpret or monitor.
An attractive alternative that allows easy inspection of the model is to directly associate each attribute or combination with the likelihoods (or propensities) mentioned above. Computing these conditional probabilities requires aggregating past data in a very simple data structure: a set of count tables, where each table associates an attribute or combination with its historical counts for each label value. The following figure illustrates two count tables in the online advertising domain:
|
|
These tables allow easily computing click probability for each seen object or combination. In the example in the table above, user Bob clicks on ads 17/(17+235)=6.75% of the time, while users entering query with hash 598fd4fe click on the ad from foo.com a whopping 30% of the time (which will be less surprising until one realizes that 598fd4fe is the hash for query foo – in which case the ad is likely ‘navigational’, providing a shortcut to the most-desired search result for the query).
These tables may remind the reader of Naïve Bayes, the classic learning algorithm that multiplies conditional probabilities for different attributes assuming their independence. While the simplicity of multiplying historical estimates is attractive, it can produce less-than-desirable accuracy when the independence assumptions are violated – as they inevitably are when the same object is involved in computing multiple estimates for different combinations. While Bayesian Networks extend Naïve Bayes by explicitly modeling relationships between attributes, they require encoding the dependency structure (or learning it), and often demand computationally expensive prediction (inference).
A slight departure from the rigor of Bayesian methods reveals a more general algorithm that maintains the simplicity of aggregating count tables, yet provides the freedom to utilize state-of-the-art algorithms such as boosted trees or neural networks to maximize the overall predictive accuracy. Instead of multiplying probabilities obtained from each table, one can choose to treat them as features – along with the raw per-label counts (or any transform thereof).
Going back to the example above, the feature vector for estimating Bob’s probability to click on the bar.org ad for query 50fa3cc0 is {17; 235; 0.0675; 497; 10984; 0.045} – simply a concatenation of the counts and resulting probabilities. This representation can be used to train a powerful discriminative learner (such as boosted trees), which has the capacity to take into account all conditional probabilities, as well as the strength of evidence behind them (corresponding to actual counts). As done in Bayesian methods, probabilities are typically adjusted via standard smoothing techniques, such as adding pseudocounts based on priors.
One may wonder how this algorithm can work in domains where millions or billions of objects exist: wouldn’t we need extremely large tables, particularly for combinations that may be very rare? The method scales via two approaches that preserve most useful statistical information by combining rare-item counts deterministically or statistically: compressing the tables either via back-off, or via count-min sketches. Back-off is the simpler of the two: it involves including only rows that have some minimal number of counts, also keeping a single “back-off bin” where the counts for the rest are combined. An additional binary feature can then be added to the representation to differentiate between attribute values for which counts were stored, versus those that were looked up in the back-off bin. The alternative to back-off is count-min sketch – an elegant technique that was invented just over a decade ago. It stores the counts for each row in multiple hash tables indexed by independent hashing functions. The impact of collisions is reduced by taking the smallest of counts retrieved via the different hashes.
Next, we turn to Azure ML to summarize the algorithm and illustrate its basic use, as shown in the following screenshot from Azure ML Studio:
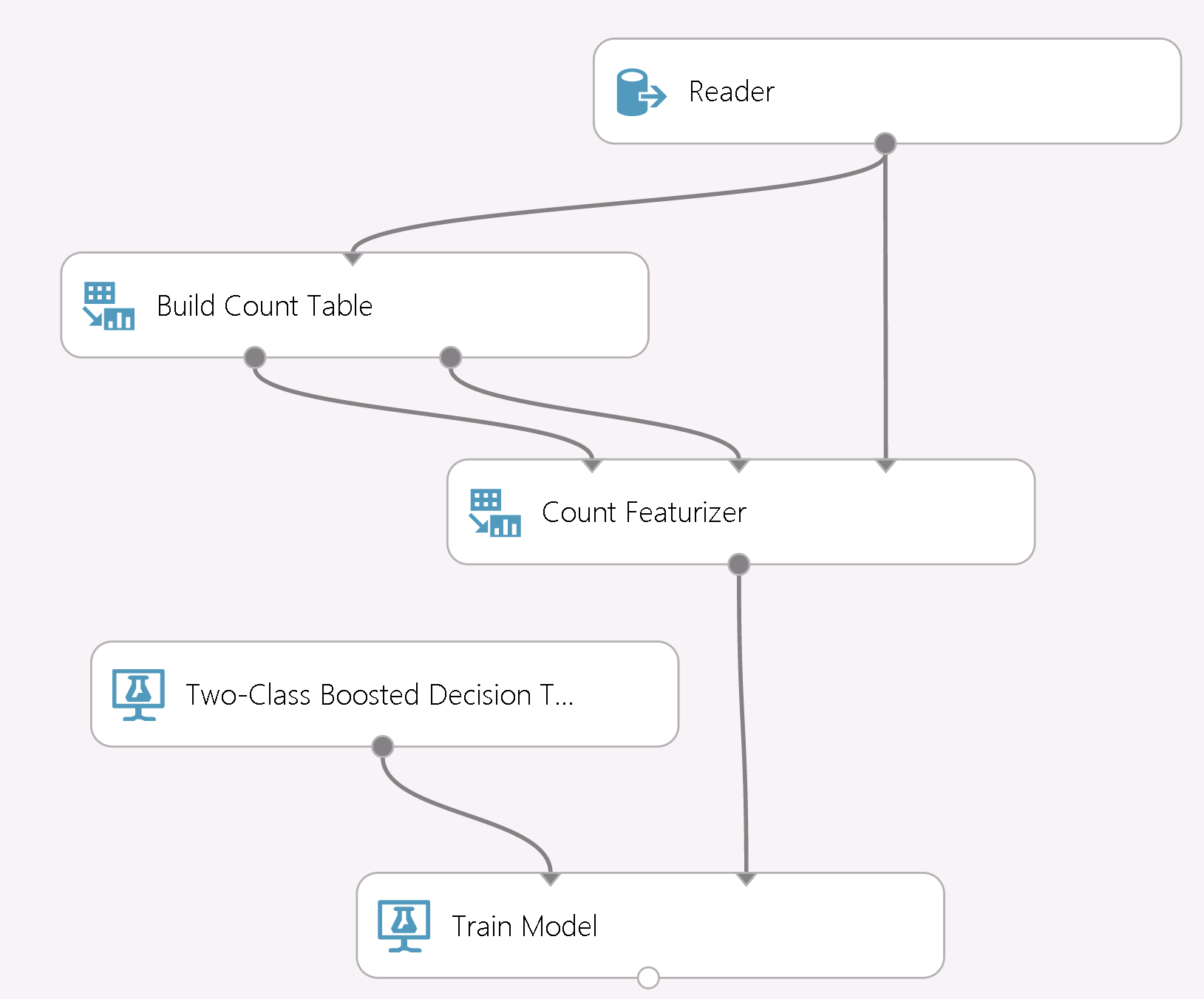
Data is input via the Reader module and passed to the Build Count Table module, which aggregates the statistics for specified attributes. The tables (along with metadata for smoothing) are then sent to the Count Featurizer module, which injects the count-based statistics and passes the resulting data representation to train boosted trees downstream. We note that the algorithm is not limited to binary classification: one can use it for regression or multi-class classification as well – the only difference being that instead of two count cells, more are needed, corresponding to discretization of the numeric label or multiple categories, respectively.
We conclude this post by summarizing the key benefits of learning with counts that made it so popular in the industry.
First and foremost, the algorithm is simple to understand, inspect and monitor: whenever one desires to perform root-cause analysis for a particular prediction, they can directly examine the evidence supplied by the count tables for each attribute or combination.
Second, the algorithm is highly modular in multiple aspects. It provides modeling modularity: one can experiment with different downstream learners utilizing the same tables, or construct multiple tables using different back-off parameters. It also provides modularity with respect to data: counts aggregated from multiple slices of data or different time periods can be added (or subtracted to remove problematic data).
It also provides elasticity to high data cardinality by automatically compressing tables using either back-off or count-min sketches.
Finally, the algorithm is very well-suited for scaling out, as the count table aggregation is a classic map-reduce computation that can be easily distributed.
In follow-up posts, we will discuss how the algorithm can be scaled out via Azure ML’s integration with HDInsight (Hadoop) to easily learn from terabytes of data, as well as techniques for avoiding overfitting and label leakage.
Misha
Comments
- Anonymous
February 17, 2015
I think there's a typo in the text at is {17; 735; 0.0675; 497; 10984; 0.045} it should have been 235 if the numbers are to match the table data. - Anonymous
February 18, 2015
Are we planning to build a tutorial for this? Would be a great starting point. - Anonymous
February 18, 2015
@Simon - you're right, this is 235 and we've fixed it, thanks for flagging the typo.