クォータニオンの使いどころ
クォータニオンでボーン処理、その3:クォータニオンの使いどころ
前回はXNAフレームワーク内での基本的なクォータニオンの使い方、特にクォータニオンは回転行列の代わりに使えるといったことを紹介しました。ただ、それだけではクォータニオンを使いたいと思った人は少ないと思います。そこで今回はクォータニオン特有の利点と、ゲームでの実際の使用方法を紹介します。
今回紹介するクォータニオンの特徴は以下の五つです
- メモリ使用量が3x3の回転行列の半分以下になる
- 回転の結合が容易にできる
- 回転の補間が容易にできる
- 正規化ができる
- 行列への変換がオイラー角を使うのに比べて高速
メモリ使用量を減らす
メモリの使用量については特に大量の容量を必要とするアニメーションデータを減らす目的でクォータニオンが使われることが多いです、Brute Forceではメインキャラクター4体のアニメーションだけで約2時間近いデータがありました。このデータを単純に4x4の行列で持つと14MB以上になりますが、クォータニオンと移動の組み合わせにすると5.6MBと、半分以下のサイズになり、更にクォータニオン内のx,y,z,wの値の範囲は-1~1までなので、それを量子化してそれぞれの要素を16ビットと半分のサイズにすることで、4.5MBと元の3分の1以下のサイズに減らしていました。
これでもXbox 1のメインメモリの64MBの7%近くを使用していたので、いつもアニメーターの人とプログラマーの間で「もっとアニメーションを増やしたい」「ダメ、メモリ足りない」というやり取りがしばしばありました。
回転の結合が容易にできる
回転の結合についてですが、例えばフライトシミュレーター系のゲームを作っている場合、現在の飛行機の姿勢を保持しておいて、コントローラーによってフレーム毎のヨー、ピッチ、ロールの差分を現在の姿勢と結合することで飛行機の姿勢を変更します。
// コントローラーによるヨー、ピッチ、ロールの取得
float dt = (float)gameTime.ElapsedGameTime.TotalSeconds;
float factor = MathHelper.ToRadians(180.0f) * dt;
float yaw = (padState.Triggers.Left - padState.Triggers.Right) * factor;
float pitch = padState.ThumbSticks.Left.Y * factor;
float roll = padState.ThumbSticks.Left.X * factor;
// 行列を使った姿勢変更
Matrix deltaMtx = Matrix.CreateFromYawPitchRoll(yaw, pitch, roll);
rotationMatrix = rotationMatrix * deltaMtx;
// クォータニオンを使った姿勢変更
Quaternion deltaQuat = Quaternion.CreateFromYawPitchRoll(yaw, pitch, roll);
rotationQuaternion = Quaternion.Concatenate(rotationQuaternion, deltaQuat);
// クォータニオンの正規化
rotationQuaternion.Normalize();
行列でも回転の結合ができるのですが、行列の場合、単精度浮動小数点(float)の誤差が計算ごとに溜まっていき、最終的には正常な回転行列ではなくなってしまうという問題があります。そこで、正規化を使うことで計算誤差でおかしくなった回転状態を簡単に正常に戻すことのできるクォータニオンです。
と、書きたかったのですが、よくよく考えるとXNAフレームワークを使っている場合、計算自体はXbox 360、Windows上のどちらでも倍精度(double)で行われるので、あんまり問題ありませんでした。ちなみに、単精度の計算すると60fpsのゲームで3分後くらいにモデルの形状がおかしくなってしまうという問題がありました。
そこで、プログラムのアップデート内で実際の速度の3,000倍の速さで更新するプログラムを作って試してみました。下はプログラムを実行し始めてから三時間経過した時の様子です。左側は行列で回転の結合をしただけのもの、右側はクォータニオンを使って結合、正規化をしたものです。左側の機体が右側の機体よりも大きくなっているのが分かると思います。これは、回転行列の結合を続けることで浮動小数点の誤差が積み重なって、正しい回転行列ではなくなってしまったという証拠です。
 ただし、前述のようにこのプログラムは本来の3000倍の速度で動作しているので、実際の時間に換算して1年になるので、XNAフレームワークをWindows, Xbox 360上で使っている限りは問題ありませんが、XNAフレームワーク以外で単精度の浮動小数点を使っている場合は精度の問題が発生するので、クォータニオンを使って回転の結合をした後に正規化をすることによって、この誤差を修正することができます。
ただし、前述のようにこのプログラムは本来の3000倍の速度で動作しているので、実際の時間に換算して1年になるので、XNAフレームワークをWindows, Xbox 360上で使っている限りは問題ありませんが、XNAフレームワーク以外で単精度の浮動小数点を使っている場合は精度の問題が発生するので、クォータニオンを使って回転の結合をした後に正規化をすることによって、この誤差を修正することができます。
回転の補間が容易にできる
次にクォータニオンを使う醍醐味と言っていいほどの特徴が回転の補間です。オイラー角を使った場合、ひとつの軸のに対しての回転であれば回転の補間はできますが、自由な回転同士の補間は不可能です。それに対して、クォータニオンを使った場合はどんな回転の状態であれ、簡単に補間することができます。
また、スキンアニメーションなどで複数の行列をブレンドしている、つまり補間していますが、これは線形補間でしかないので回転が含まれている行列同士の補間では厳密には正確な補間ができないのですが、スキンアニメーションのボーンブレンディングの場合は誤差が無視できる範囲でブレンディングが行われるので殆どの場合は問題ないように見えているというのが現状です。
クォータニオンの補間にはLerp(ラープ)、Slerp(スラープ)を使って簡単に正確な回転補間ができます。ちなみにLerpはLinear Interporationの略で日本語では線形補間、SlerpはSphercal Linear Interpolationの略で、日本語では球面線形補間となります。
下は0度回転の状態と90度回転したものを補間するコードです。ここではSlerpを使っていますが、この場合では線形補間であるLerpを使っても問題ありません。線形とは言ってもクォータニオンの世界のなかの線形であって、3次元空間の線形とは違います。クォータニオンのLerpとSlerpでは前者の方が計算が軽いですが、誤差が発生してしまいます。Brute Forceでは計算速度を稼ぐために回転角度が大きく違う時以外はLerpを使い、誤差を修正するために時々正規化していました。
// 0度と90度回転の行列とクォータニオンの生成
Matrix mtx0 = Matrix.CreateRotationZ(MathHelper.ToRadians(0));
Matrix mtx1 = Matrix.CreateRotationZ(MathHelper.ToRadians(90));
Quaternion q0 = Quaternion.CreateFromAxisAngle( Vector3.UnitZ, MathHelper.ToRadians(0));
Quaternion q1 = Quaternion.CreateFromAxisAngle(Vector3.UnitZ, MathHelper.ToRadians(90));
// 補間
Matrix m = Matrix.Slerp(mtx0, mtx1, t);
Quaternion q = Quaternion.Lerp(q0, q1, t);
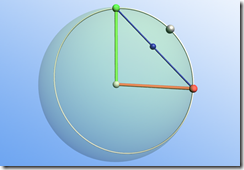
コードだけでは、実際にどのように補間されているの分からないので、テストプログラムを使って動画にしてみました。赤い軸が0度の地点、緑の軸が90度回転した位置を表しています。青い点は行列の補間の結果で、白い点はクォータニオンの補間の結果になります。
クォータニオンの補間では白い点が綺麗に円弧を描いているのに対して、行列の変換では青い点が直線的に動いているのが分かると思います。
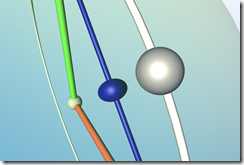
また、拡大してみると判りますが、クォータニオンでの補間だと問題ありませんが、行列の補間の場合だと形がゆがんでいます。動画を見ると、このゆがみは補完する中間地点に近づくほどに大きくなり、始点と終点付近で元に戻っている様子がわかると思います。
このように、行列の線形補間は回転の補間が苦手ということがわかったと思います。アニメーションデータの容量を少なくするためにキーフレーム間の補間をするときがありますが、すばやい回転アニメーション、例えば野球選手の投球モーションの腕の部分のように短い時間で大きな回転動作をする場合に行列の線形補間を使うと、回転モーションが正しく保管されずに縮こまった投球モーションになってしまいます。そこでクォータニオンを使えば少ないアニメーションデータでも綺麗な投球モーションになります。
正規化ができる
これは既に上で何度か説明していますが、浮動小数点による計算誤差や、Lerpを使った時などに回転状態が徐々に崩れていってしまうという問題があるのですが、クォータニオンの場合は単純にQuaternion.Normalizeを呼び出すだけで簡単に正常な回転状態に戻すことができます。
この正常な状態に戻せるというのは重要なことで、実際にゲームを作っていると最初プレイしているうちは滑らかに動いていたのに、時間が経つとガクガクしてくるという問題に直面することがあり、その原因が精度の問題だった場合、原因を突き止めるのが非常に困難になるので、こういった問題が発生する前から誤差があっても動作するコードが書けるというのは時間の節約にもなります。
行列への変換がオイラー角を使うのに比べて高速
例えば爆破などのエフェクトで回転しながら飛び散る破片があるとします。この時に、X,Y,Zのオイラー角を使って実装した場合、フレーム毎に描画する前に行列に変換しないといけませんが、その変換過程で計算に時間の掛かるSin,Cosの三角関数が使用されます。それに対して、クォータニオンの場合は最初に回転速度を表すクォータニオンを生成しておけば、フレーム毎の更新では現在の姿勢を示すクォータニオンと結合するだけですみます。この結合とクォータニオンから行列への変換は計算時間の掛からない単純な積和演算だけで済むのでむので大量のオブジェクトを処理するときに有用です。
クォータニオンを使う目安
三回に渡ってクォータニオンの特徴を説明してきましたが、最後にクォータニオンをいつ使うべきかを判断するポイントを紹介します。
クォータニオンを使うと便利
アニメーションデータが多すぎるので圧縮したい
- キーフレーム間の回転補間
自由に回転状態を変化させたい
- 岩などのオブジェクトが地面の起伏の状態によって回転状態が変化する場合
- 飛行機などの姿勢制御
回転状態を変化させる必要はないけど対象となるオブジェクトが大量にある
- 爆発などで大量の破片がランダムに回転しながら飛び散るエフェクト
オイラー角で十分
制限された回転
- FPS、TPSなどのカメラコントロール
回転状態を変化する必要がない
- 爆発などで少数の破片がランダムに回転しながら飛び散るエフェクト
誤差があっても大丈夫
- 回転の結合が短時間だけ必要な場合、上記のエフェクトなどカットシーン的な場面で使われる回転
次は、いよいよ(やっと?)クォータニオンを使ったボーン数節約の実装例を紹介します。