DAG: más allá de la “A”
Artículo original publicado el viernes 16 de septiembre de 2011
Definiciones
Todos sabemos que, en el mundo de Microsoft Exchange, DAG significa “Database Availability Group” (Grupo de disponibilidad de base de datos).
Base de datos: porque en un servidor de alta disponibilidad de buzones de correo de Exchange 2010, la base de datos, no el servidor, es la unidad de disponibilidad y es la base de datos que puede conmutarse por error o conmutarse entre varios servidores dentro de un DAG. Este concepto se conoce como movilidad de base de datos.
Grupo: porque el ámbito de disponibilidad está determinado por los servidores de buzones de correo en un DAG combinado en un clúster de conmutación por error y que funcionan conjuntamente como grupo.
Disponibilidad: esta palabra parece que es el término menos obvio y el más confuso de todos (y al que hacen referencia ambos términos). Irónicamente, tiene una definición matemática sencilla y tiene un rol importante para entender los principios generales del diseño de Exchange.
Wikipedia define “disponibilidad” de modo que tiene uno de los significados siguientes:
- El grado en que un sistema, subsistema o equipo está en un estado ejecutable y confirmable específico al comienzo de una misión cuando se solicita la misión en un momento desconocido, es decir, aleatorio. Dicho de manera sencilla, la disponibilidad es la proporción de tiempo durante la cual un sistema se encuentra en estado de funcionamiento. Esto se describe a menudo como una tasa de capacidad de realizar una misión. Matemáticamente, esto se expresa como 1 menos no disponibilidad.
- La relación entre (a) el tiempo total que una unidad funcional se puede usar durante un intervalo determinado y (b) la longitud del intervalo.
Usando términos de la teoría de la probabilidad, estas definiciones significan lo mismo: la probabilidad de que un sistema o componente determinado esté “ejecutable” o sea “capaz de usarse” (es decir, disponible) en un momento de tiempo aleatorio (cuando lo probemos).
Matemáticamente, esto se puede medir calculando la cantidad de tiempo en que el sistema está disponible (“tiempo activo”) durante un largo período representativo estadísticamente (normalmente un año), y dividiéndolo por la longitud total del período. Usando los términos ampliamente adoptados de Tiempo medio entre errores (MTBF) y Tiempo medio de reparación (MTTR) –el primero representa la disponibilidad/el tiempo activo del sistema entre los errores, mientras que el último representa el tiempo de inactividad del sistema durante cualquier error determinado–, la disponibilidad se puede expresar como una fracción:
La característica matemática contraria sería una probabilidad de error (considerada como “no disponibilidad”):
La disponibilidad se expresa a menudo como una “serie de nueves”, de acuerdo con la tabla siguiente:
Nivel de disponibilidad |
Valor de disponibilidad |
Probabilidad de error |
Tiempo de inactividad aceptado por año |
Dos nueves |
99% |
1% |
5.256 minutos = 3,65 días |
Tres nueves |
99,9% |
0,1% |
525,6 minutos = 8,76 horas |
Cuatro nueves |
99,99% |
0,01% |
52,56 minutos |
Cinco nueves |
99,999% |
0,001% |
5,26 minutos |
Por supuesto, el valor de disponibilidad sería diferente en función de si se tiene en cuenta el tiempo de inactividad programado (planeado) y no programado (no planeado) o solo el tiempo de inactividad no programado. El contrato de nivel de servicio que representa los requisitos de disponibilidad empresarial debe ser muy específico al respecto. Pero en todos los casos la disponibilidad de un sistema o componente determinado depende de muchos factores y es muy importante identificar y comprender las dependencias y cómo afectan estas a la disponibilidad.
Cómo afectan a la disponibilidad las dependencias de servicios
La disponibilidad de una base de datos de buzones de correo de Exchange depende de la disponibilidad de muchos otros servicios y componentes; por ejemplo, el subsistema de almacenamiento que hospeda la base de datos, el servidor que opera esta base de datos, la conectividad de red a este servidor, etc. Todos estos componentes son críticos, y el error de uno de ellos significaría la pérdida de servicio incluso si la propia base de datos está en perfecto estado. Esto significa que para que la base de datos esté disponible como un servicio, cada dependencia de la base de datos también debe estar disponible. Si identificamos y aislamos adecuadamente los componentes en dependencia, podemos calcular matemáticamente cómo estos determinan la disponibilidad resultante de la propia base de datos de buzones de correo de Exchange.
Para una determinada base de datos de buzones de correo de Exchange, los siguientes componentes se pueden considerar dependencias críticas:
- Subsistema de almacenamiento/disco de la base de datos: supongamos que su disponibilidad es A1;
- Servidor de buzones de correo (componentes de hardware y de software): supongamos que su disponibilidad es A2;
- Servidor de acceso de cliente (componentes de hardware y de software): recuerde que en Exchange 2010 todos los clientes se conectan a la base de datos de buzones de correo solo a través del servidor de acceso de cliente, y asumamos que el CAS está instalado de manera independiente al servidor de buzones de correo en este caso: supongamos que su disponibilidad es A3;
- Conectividad de red entre clientes y el servidor de acceso de cliente y entre el servidor de acceso de cliente y el servidor de buzones de correo: supongamos que su disponibilidad es A4;
- Potencia en el centro de datos donde se ubican los servidores y el almacenamiento: supongamos que su disponibilidad es A5;
Esta lista podría continuar… Por ejemplo, Active Directory y DNS también representan una dependencia crítica para Exchange. Además, aparte de las dependencias tecnológicas puras, la disponibilidad está afectada por dependencias de procesos como la madurez operativa, etc.: los errores humanos, las operaciones definidas incorrectamente o la falta de coordinación de los equipos podrían provocar la inactividad del servicio. No intentaremos recopilar una lista exhaustiva de dependencias sino que nos centraremos en cómo afectan estas a la disponibilidad general del servicio.
Puesto que estos componentes son independientes individualmente entre sí, la disponibilidad de cada uno de ellos representa un evento independiente, y la disponibilidad resultante de una base de datos de buzones de correo de Exchange representa una combinación de todos estos eventos (en otras palabras, para que una base de datos de buzones de correo esté disponible para los clientes, todos estos componentes deben estar disponibles). En la teoría de la probabilidad, la probabilidad de una combinación de eventos independientes es un producto de las probabilidades individuales para cada evento:
Por ejemplo, si lanzase tres monedas, la probabilidad de que salga cara en las tres monedas es (1/2)*(1/2)*(1/2) = 1/8.
Es importante tener en cuenta que, puesto que cada valor de disponibilidad individual no puede ser mayor que 1 (o 100%), y que la disponibilidad del servicio resultante es simplemente un producto de las disponibilidades de los componentes individuales, el valor de la disponibilidad resultante no puede ser mayor que la menor de las disponibilidades de los componentes dependientes.
Esto se puede ilustrar con el ejemplo presentado en la tabla siguiente (los números indicados son muestras pero son bastante realistas):
Componente de dependencia crítica |
Probabilidad de error |
Valor de disponibilidad |
Servidor de buzones de correo y almacenamiento |
5% |
95% |
Servidor de acceso de cliente |
1% |
99% |
Red |
0,5% |
99,5% |
Potencia |
0,1% |
99,9% |
Servicio general (depende de todos los componentes anteriores) |
6,51383% |
95% x 99% x 99,5% x 99,9% = 93,48617% |
En este ejemplo, puede ver la importancia crítica de las dependencias de servicio. Incluso para una base de datos de buzones de correo que nunca provoca errores (nunca se corrompe y nunca recibe ninguna infección de virus, etc.), la disponibilidad permanece por debajo del 93,5%.
Conclusión: un número grande de dependencias de servicio disminuye la disponibilidad.
Cualquier cosa que pueda hacer para reducir el número o el impacto de las dependencias de servicio afectará positivamente a la disponibilidad del servicio general. Por ejemplo, puede mejorar la madurez operativa simplificando y asegurando la administración del servidor y optimizando los procedimientos operativos. En el aspecto técnico, puede intentar reducir el número de dependencias de servicio simplificando su diseño: por ejemplo, eliminando el diseño complejo de almacenamiento basado en SAN, incluyendo las tarjetas de HBA, los conmutadores de fibra, los controladores de la matriz e incluso los controladores RAID, y sustituyéndolo por un diseño sencillo de DAS con un mínimo de piezas móviles.
Solo la reducción de dependencias de servicio puede no ser suficiente para obtener el nivel deseado de disponibilidad. Otra manera muy eficiente de aumentar la disponibilidad resultante y minimizar el impacto de las dependencias de servicio críticas es sacar provecho de varios métodos de redundancia como el uso de sistemas de alimentación duales, tarjetas de red unidas, la conexión de servidores a varios conmutadores de red, el uso de protección RAID para el sistema operativo, la implementación de equilibradores de carga para servidores de acceso de cliente y varias copias de bases de datos de buzones de correo. Pero, ¿cómo aumenta exactamente la redundancia a la disponibilidad? Veamos con más detalle el equilibrado de carga y las copias múltiples de bases de datos como ejemplos importantes.
Cómo afecta la redundancia a la disponibilidad
Conceptualmente, todos los métodos de redundancia significan una cosa: hay más de una instancia del componente que está disponible y que se podría usar simultáneamente con otras instancias (como en el equilibrado de carga) o como sustituto (como en las copias múltiples de bases de datos). Supongamos que tenemos n instancias de un componente determinado (n servidores en una matriz de CAS o n copias de bases de datos en un DAG). Aunque una de ellas provoque un error, las otras instancias se pueden seguir usando y, por lo tanto, se mantiene la disponibilidad. La única situación en que se experimentará un tiempo de inactividad real es cuando todas las instancias provocan un error.
Tal como se ha definido anteriormente, la probabilidad de error de una instancia determinada es P = 1 – A. Todas las instancias son estadísticamente independientes entre sí, lo que significa que la disponibilidad o el error de cualquiera de ellas no afecta a la disponibilidad de otras instancias. Por ejemplo, el error de una copia de base datos determinada no afecta a la probabilidad de error de otra copia de esa base de datos (una posible salvedad aquí podría ser la propagación de la corrupción de la base de datos lógica de la primera copia de base de datos dañada a las otras copias, pero ignoremos este factor altamente improbable por ahora; después de todo, siempre se puede implementar una copia de base de datos retrasada o una copia de seguridad a partir de un momento específico tradicional para resolver esto).
Usando de nuevo el mismo teorema de la teoría de la probabilidad, la probabilidad de error de un conjunto de n componentes independientes es un producto de las probabilidades para cada componente. Como todos los componentes son idénticos (distintas instancias del mismo objeto), el producto se convierte en una potencia:
Aparentemente, como P < 1, Pn es menor que P, lo cual significa que la probabilidad de error se reduce, y, en consecuencia, la disponibilidad aumenta:
Consideremos un ejemplo de la vida real para verlo más claro. Supongamos que implementamos varias copias de base de datos de buzones de correo; cada copia se hospeda en una sola unidad SATA. Estadísticamente, la tasa de error de las unidades SATA es ~5% en un año[1], lo que da una probabilidad de error del 5%: P = 0,05 (lo que significa una disponibilidad del 95%: A = 0,95). ¿Cómo cambia la disponibilidad a medida que agregamos más copias de base de datos? Veamos la siguiente tabla, que debería ser explicativa:
Número de copias de base de datos |
Probabilidad de error |
Valor de disponibilidad |
1 |
P1 = P = 5% |
A1 = 1 – P1 = 95% |
2 |
P2 = P2 = 0,25% |
A2 = 1 – P2 = 99,75% |
3 |
P3 = P3 = 0,0125% |
A3 = 1 – P3 = 99,9875% |
4 |
P4 = P4 = 0,000625% |
A4 = 1 – P4 = 99,9994% |
Bastante impresionante, ¿no? Básicamente, cada copia de base de datos adicional en una unidad SATA introduce el factor de multiplicación del 5% o 1/20, de manera que la probabilidad de error es 20 veces menor con cada copia (y, en consecuencia, la disponibilidad aumenta). Puede ver que incluso con las unidades SATA menos confiables, implementar solo 4 copias de base de datos lleva la disponibilidad a cinco nueves.
Esta ya es muy buena pero, ¿se puede mejorar? ¿Se puede mejorar la disponibilidad más aún sin realizar cambios de arquitectura (por ejemplo, si no se plantea agregar otra copia de base de datos)?
En realidad, se puede. Si mejora la disponibilidad individual de cualquier componente de dependencia, aumentará la disponibilidad de servicio general y provocará un efecto más potente al agregar componentes redundantes. Por ejemplo, una manera posible de realizar esto sin tirar la casa por la ventana es usar unidades SAS Nearline en lugar de unidades SATA. Las unidades SAS Nearline tienen una tasa de error anual del ~2.75% en lugar del ~5% para SATA. Esto reducirá la probabilidad de error para el componente de almacenamiento en el cálculo anterior y, por lo tanto, aumentará la disponibilidad de servicio general. Compare el impacto de agregar copias múltiples de base de datos:
- Tasa de error anual del 5% = factor de multiplicación de 1/20 = cada copia nueva hace el error de la base de datos 20 veces menos probable.
- Tasa de error anual del 2,75% = factor de multiplicación de 1/36 = cada copia nueva hace el error de la base de datos 36 veces menos probable.
Este impacto significativo que tienen las copias de base de datos adicionales en la disponibilidad de bases de datos también explica nuestra guía acerca del uso de la protección de datos nativos de Exchange, que afirma que las copias múltiples de base de datos podrían ser el sustituto de las copias de seguridad tradicionales si se implementa un número suficiente (tres o más) de copias de base de datos.
La misma lógica se aplica a la implementación de varios servidores de acceso de cliente en una matriz de CAS, varios conmutadores de red, etc. Supongamos que hemos implementado 4 copias de base de datos y 4 servidores de acceso de cliente y revisemos la tabla de disponibilidad de componentes que analizamos anteriormente:
Componente de dependencia crítica |
Probabilidad de error |
Valor de disponibilidad |
Servidor de buzones de correo y almacenamiento (4 copias) |
5% ^ 4 = 0,000625% |
99,999375% |
Servidor de acceso de cliente (4 servidores, instalador por separado) |
1% ^ 4 = 0,000001% |
99,999999% |
Red |
0,5% |
99,5% |
Potencia |
0,1% |
99,9% |
Servicio general (depende de todos los componentes anteriores) |
0,6% |
99,399878% |
Puede ver cómo porque hemos implementado 4 servidores de acceso de cliente y 4 copias de base de datos, la probabilidad de error del servicio general se ha dividido por más de 10 (del 6,5% al 0,6%) y, en consecuencia, la disponibilidad del servicio ha aumentado del 93,5% a un valor mucho más decente como es el 99,4%.
Conclusión: agregar redundancia a las dependencias de servicio aumenta la disponibilidad.
Juntar todas las piezas
De las conclusiones anteriores surge una pregunta interesante. Hemos analizado dos factores distintos que afectan a la disponibilidad del servicio general de dos maneras distintas y hemos sacado dos conclusiones claras:
- agregar más dependencias del sistema reduce la disponibilidad
- agregar redundancia a las dependencias del sistema aumenta la disponibilidad
¿Qué ocurre si ambos son factores de una solución determinada? ¿Qué tendencias es más fuerte?
Considere el siguiente escenario:
Implementamos dos servidores de buzones de correo en un DAG con dos copias de base de datos de buzones de correo (una copia en cada servidor) e implementamos dos servidores de acceso de cliente en una matriz de carga equilibrada. (Para simplificar, solo consideraremos la disponibilidad de una base de datos de buzones de correo para conexiones de cliente, sin tener en cuenta, por ahora, el transporte de concentradores y la mensajería unificada). Suponiendo que cada servidor tiene su probabilidad de error individual de P, ¿será la disponibilidad de tal sistema mejor o mejor que la disponibilidad de un solo servidor independiente de Exchange con roles de servidor de buzones de correo y de servidor de acceso de cliente implementados?
En el primer escenario, los servidores de buzones de correo son independientes y no estarán disponibles solo si ambos servidores generan un error. La probabilidad de error para el conjunto de los dos servidores de buzones de correo será P × P = P2. En consecuencia, su disponibilidad será AMBX = 1 – P2. Siguiendo la misma lógica, los servicios de CAS no estarán disponibles solo si ambos servidores de acceso de cliente generan un error, de modo que la probabilidad de error para el conjunto de dos servidores de acceso de cliente será nuevamente P × P = P2 y, en consecuencia, su disponibilidad será ACAS = 1 – P2.
En este caso, como se habrá dado cuenta, dos servidores de buzones de correo y dos servidores de acceso de cliente son ejemplos de componentes del sistema redundantes.
Siguiendo con este escenario, a fin de que todo el sistema esté disponible, ambos conjuntos de servidores (conjunto de servidores de buzones de correo y conjunto de servidores de acceso de cliente) deben estar disponibles simultáneamente. No generar error simultáneamente sino estar disponible simultáneamente, porque ahora representan dependencias del sistema en lugar de componentes redundantes. Esto significa que la disponibilidad del servicio general es un producto de las disponibilidades para cada conjunto:
Por supuesto, el segundo escenario es mucho más sencillo ya que solo hay un servidor a tener en cuenta, y su disponibilidad es simplemente A = 1 – P.
Ahora que hemos calculados los valores de disponibilidad para ambos escenarios, ¿qué valor es mayor (1-P2)2 o 1-P?
Si trazamos los gráficos de ambas funciones, se observa el siguiente comportamiento:
(Usé el motor de cálculo gratuito Wolfram Alpha Mathematica Online para realizar el trazado de manera rápida y sencilla).
Podemos observar que para los valores pequeños deP, la disponibilidad del sistema complejo de 4 servidores es mayor que la disponibilidad del servidor único. No hay sorpresa; eso es lo que esperábamos, ¿verdad? Sin embargo, en P ~ 0,618 (más precisamente, 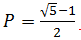 ) los dos trazados se cruzan, y para valores mayores de P el sistema de un único servidor tiene una mayor disponibilidad. Por supuesto, se podría esperar que el valor de P fuera cercano a cero en la vida real; sin embargo, si prevé crear su solución a partir de componentes muy poco confiables, probablemente le iría mejor con un único servidor.
) los dos trazados se cruzan, y para valores mayores de P el sistema de un único servidor tiene una mayor disponibilidad. Por supuesto, se podría esperar que el valor de P fuera cercano a cero en la vida real; sin embargo, si prevé crear su solución a partir de componentes muy poco confiables, probablemente le iría mejor con un único servidor.
Impacto de los dominios de error
Desafortunadamente, los escenarios de implementación en la vida real son raramente tan sencillos como las situaciones tratadas anteriormente. Por ejemplo, ¿cómo cambia la disponibilidad del servicio si implementa servidores de varios roles? Observamos en el escenario anterior que combinar los roles de servidor reduce de manera efectiva el número de dependencias de servicio, por lo que, ¿sería algo bueno? ¿Qué ocurre si coloca dos copias de base de datos de la misma base de datos en la misma matriz de SAN o en un recinto de DAS? ¿Qué ocurre si todos sus servidores de buzones de correo están conectados al mismo conmutador de red? ¿Qué ocurre si se dan las condiciones anteriores y más?
Todas estas situaciones tienen que ver con el concepto de dominios de error. En los ejemplos anteriores, el hardware del servidor, o una matriz de SAN, o un conmutador de red representan un dominio de error. Un dominio de error rompe la independencia o la redundancia de los componentes que combina: por ejemplo, el error del hardware del servidor en un servidor de varios roles significa que todos los roles de Exchange estarán no disponibles; en consecuencia, el error de un recinto de disco o de una matriz de SAN significa que todas las copias de base de datos hospedadas en este recinto o matriz estarán no disponibles.
Los dominios de error no son necesariamente algo malo. La diferencia importante es qué tipo de componentes constituyen un dominio de error: ¿son dependencias del sistema distintas o son componentes del sistema redundantes? Consideremos dos de los ejemplos anteriores para entender esta diferencia.
Escenario de servidor de varios roles
Comparemos la disponibilidad de los distintos sistemas:
- Los roles de servidor de buzones de corrreo y de acceso de cliente hospedados en el mismo servidor que tiene la probabilidad de error de hardware de P;
- Los mismos roles hospedados en dos servidores independientes, cada uno con la misma probabilidad de error de hardware;
En el primer caso, el hardware de un único servidor representa un dominio de error. Esto significa que todos los roles hospedados están o disponibles o no disponibles. Esto es sencillo; la disponibilidad general de tal sistema es A = 1 – P.
En el segundo caso, el servicio general estará disponible solo cuando ambos servidores estén disponibles de manera independientemente (porque cada rol representa una dependencia crítica). Por lo tanto, según la teoría de la probabilidad, su disponibilidad será A × A = A2.
Nuevamente, como A < 1, significa que A2 < A, de manera que en el segundo caso la disponibilidad será inferior.
Aparentemente, podemos agregar otros roles de servidor de Exchange (Transporte de concentradores y Mensajería unificada si es necesario) al mismo escenario sin romper esta lógica.
Conclusión: colocar roles de servidor de Exchange en un servidor de varios roles aumenta la disponibilidad del servicio general.
Escenario de almacenamiento compartido
Ahora consideremos otro escenario de dominio de error (dos copias de base de datos que comparten la misma matriz de almacenamiento) y comparemos la disponibilidad de base de datos en los dos casos siguientes:
- Dos copias de base de datos hospedadas en el mismo almacenamiento compartido (matriz de SAN o recinto de DAS), que tiene la probabilidad de error de P;
- Las mismas copias de base de datos hospedadas en dos sistemas de almacenamiento separados, cada una con la misma probabilidad de error;
En el primer caso, el almacenamiento compartido representa un dominio de error. Como en el escenario anterior, esto significa que ambas copias de base de datos están disponibles o no disponibles simultáneamente, de modo que la disponibilidad general vuelve a ser A = 1 – P.
En el segundo caso, el servicio general estará disponible si al menos un sistema está disponible, y no disponible solo si ambos sistemas generan un error. Los sistemas de almacenamiento en cuestión son independientes; por lo tanto, la probabilidad de error para el servicio general es P × P = P2 y, en consecuencia, la disponibilidad del servicio general es A = 1 – P2.
Nuevamente, como P < 1, significa que P2 < P y, por lo tanto, 1 – P2 > 1 – P. Esto significa que la disponibilidad en el segundo caso es mayor.
Conclusión: colocar copias de base de datos en el mismo sistema de almacenamiento disminuye la disponibilidad del servicio general.
Entonces, ¿cuál es la diferencia entre estos dos escenarios? ¿Por qué la introducción de un dominio de error aumenta la disponibilidad en el primer caso y la reduce en el segundo?
Esto se debe a que el dominio de error en el primer caso combina dependencias del servicio, de modo que reduce de forma efectiva su número y, por lo tanto, mejora la disponibilidad, mientras que el dominio de error en el segundo caso combina componentes redundantes, de modo que reduce de manera efectiva la redundancia y, por lo tanto, afecta a la disponibilidad.
Estos conceptos y conclusiones se podrían visualizar probablemente de la manera siguiente:
(No, no usamos Wolfram Alpha para trazar este gráfico)
Resumen
La arquitectura de Exchange 2010 proporciona posibilidades potentes para agregar redundancia a nivel de Exchange (como la implementación de varias copias de base de datos o varios servidores de acceso de cliente en una matriz de CAS) y para reducir el número de dependencias del sistema (combinando roles de servidor de Exchange en un servidor de varios roles o usando una arquitectura de almacenamiento más sencilla sin un número excesivo de componentes críticos). Las sencillas reglas y fórmulas que se presentan en este artículo permiten calcular el efecto sobre el valor de disponibilidad a partir de implementar copias de base de datos adicionales o de combinar roles de servidor de Exchange; también puede calcular el impacto de los dominios de error. Es importante tener en cuenta que intentamos usar estos modelos matemáticos sencillos para ilustrar los conceptos, no para intentar obtener valores de disponibilidad precisos. La vida real raramente se corresponde con los sencillos escenarios básicos, y se necesitan cálculos mucho más complejos para obtener estimaciones razonables para la disponibilidad de sus sistemas reales; podría ser más fácil medir simplemente la disponibilidad a nivel estadístico y comprobar si satisface los requisitos del SLA. Sin embargo, entender los factores que afectan a la disponibilidad y cómo influyen en su conjunto en una solución de ingeniería compleja debería ayudarle a diseñar la solución correctamente y conseguir un aumento significativo de la disponibilidad del servicio general, y satisfacer los requisitos empresariales más exigentes.
Boris Lokhvitsky
Arquitecto de entrega
[1] Los siguientes estudios realizados por la Carnegie Mellon University, Google y Microsoft Research muestran la tasa de error anual del 5% para unidades SATA:
https://www.usenix.org/events/fast07/tech/schroeder/schroeder.pdf
https://labs.google.com/papers/disk_failures.pdf
https://research.microsoft.com/research/pubs/view.aspx?msr_tr_id=MSR-TR-2005-166
Esta es una entrada de blog localizada. Puede encontrar el artículo original en DAG: Beyond the “A”








