DAG: além do “A”

Artikkeli
11/22/2011

Artigo original publicado em 16 de setembro de 2011, sexta-feira.

Definições

Todos nós sabemos que no mundo do Microsoft Exchange DAG significa “Grupo de Disponibilidade de Banco de Dados”.

Banco de dados – porque em um servidor de caixa de correio do Exchange 2010 altamente disponível, o banco de dados, não o servidor, é a unidade de disponibilidade e é o banco de dados que pode falhar ou alternar entre vários servidores dentro de um DAG. Esse conceito é conhecido como mobilidade do banco de dados.

Grupo – como o escopo de disponibilidade é determinado pelos servidores da caixa de correio em um DAG combinado em um cluster de failover e trabalhando junto como um grupo.

Disponibilidade – essa palavra parece ser a menos óbvia e o termo mais ofuscado aqui (e também referido por ambos os outros termos). Ironicamente, isso tem uma definição matemática simples e tem um papel importante na compreensão geral dos princípios do design do Exchange.

A Wikipedia define “disponibilidade como o seguinte:

O grau em que um sistema, subsistema ou equipamento está em um estado confirmável e operável especificado no início de uma missão, quando a missão é solicitada a um desconhecido, ou seja, um tempo aleatório. Simplificando, disponibilidade é a proporção de tempo e que um sistema está na condição de funcionamento. Isso é frequentemente descrito como uma taxa de missão capaz. Matematicamente, ela é expressa como 1 menos indisponibilidade.
A proporção do (a) tempo total que uma unidade funcional é capaz de ser usada durante um determinado intervalo para (b) a duração do intervalo.

Usando os termos da teoria da probabilidade, ambas as definições significam a mesma coisa: probabilidade que um determinado sistema ou componente seja “operável” ou “capaz de ser usado” (ou seja, disponível) em um momento aleatório do tempo (quando testamos).

Matematicamente isso pode ser medido calculando a quantidade de tempo quando o sistema está disponível (“duração do serviço”) durante algum período estendido representativo estatisticamente (em geral, um ano), e dividindo pela duração total do período. Usando termos amplamente adotados de Tempo de Intervalo entre Falhas (MTBF) e Tempo de Intervalo para Reparo (MTTR) – o primeiro representa a disponibilidade/duração do serviço do sistema entre as falhas, enquanto o último representa o tempo de inatividade do sistema durante qualquer falha determinada, – disponibilidade pode ser expressa como uma fração:

A característica matemática oposta seria uma probabilidade de falha (pense em “não disponibilidade”):

A disponibilidade frequentemente é expressa como “número de noves”, de acordo com a tabela a seguir:

Nível da disponibilidade	Valor da disponibilidade	Probabilidade de falha	Tempo de inatividade aceito por ano
Dois noves	99%	1%	5.256 minutos = 3,65 dias
Três noves	99,9%	0,1%	525,6 minutos = 8,76 horas
Quatro noves	99,99%	0,01%	52,56 minutos
Cinco noves	99,999%	0,001%	5,26 minutos

É claro que o valor da disponibilidade seria diferente, dependendo se considerarmos o tempo de inatividade programado (planejado) e não programado (não planejado) ou basta apenas o tempo de inatividade não programado. O Contrato de Nível de Serviço que representa os requisitos de disponibilidade comercial deve ser muito específico sobre isso. Mas em todos os casos a disponibilidade de qualquer sistema ou componente determinado depende de muitos fatores e é absolutamente importante identificar e compreender essas dependências e como elas causam impacto na disponibilidade.

Como as dependências do serviço causam impacto na disponibilidade

A disponibilidade do banco de dados da caixa de correio do Exchange depende da disponibilidade de muitos outros serviços e componentes – por exemplo, o subsistema de armazenamento que hospeda o banco de dados, o servidor que opera esse banco de dados, a conectividade da rede para esse servidor, etc. Todos esses são componentes essenciais, e a falha em um único deles pode significar a perda do serviço, mesmo se o próprio banco de dados estiver em perfeitas condições. Isso significa que para o banco de dados estar disponível como um serviço, cada dependência única do banco de dados deve estar disponível também. Se identificarmos e isolarmos corretamente os componentes de dependência, podemos calcular matematicamente como eles determinam a disponibilidade resultante do próprio banco de dados da caixa de correio do Exchange.

Para um determinado banco de dados da caixa de correio do Exchange, os seguintes componentes podem ser considerados dependências críticas:

Disco do banco de dados/subsistema de armazenamento – vamos dizer que sua disponibilidade é A₁;
Servidor da caixa de correio (ambos os componentes de hardware e software) – dizemos que sua disponibilidade é A₂;
Servidor de acesso para cliente (ambos os componentes de hardware e software) – lembre-se de que todos os clientes do Exchange 2010 se conectam ao banco de dados da caixa de correio somente via Servidor de acesso para cliente, e vamos supor que o CAS esteja instalado separadamente a partir do servidor da caixa de correio nesse caso – sua disponibilidade é A₃;
Conectividade de rede entre clientes e o servidor de Acesso do cliente e entre o servidor de Acesso do cliente e o servidor de caixa de correio – sua disponibilidade é A₄;
Potência no datacenter onde os servidores e o armazenamento estão localizados – sua disponibilidade é A₅;

Essa lista poderia continuar… Por exemplo, Active Directory e DNS representam a dependência crítica também parra o Exchange. E mais, além das dependências tecnológicas puras, a disponibilidade é influenciada por dependências do processo, como maturidade operacional e assim em diante: erro humano, operações definidas incorretamente, falta de coordenação da equipe, todos poderiam levar a inatividade do serviço. Não tentaremos compilar nenhuma lista extensa de dependências, mas em vez disso nos concentramos em como elas causam impacto na disponibilidade geral do serviço.

Como esses componentes são individualmente independentes uns dos outros, a disponibilidade de cada um representa um evento independente, e a disponibilidade resultante de um banco de dados da caixa de correio do Exchange representa uma combinação de todos esses eventos (em outras palavras, para um banco de dados da caixa de correio ficar disponível para os clientes todos esses componentes devem estar disponíveis). Na teoria da probabilidade, a probabilidade de uma combinação de eventos independentes é um produto das probabilidades individuais de cada evento:

Por exemplo, se você jogar três moedas, a probabilidade de obter caras em todas as três moedas é (1/2)*(1/2)*(1/2) = 1/8.

É importante perceber que como cada valor da disponibilidade individual não pode ser superior a 1 (ou 100%), e a disponibilidade do serviço resultante é simplesmente um produto das disponibilidades do componente individual, o valor da disponibilidade resultante não pode ser superior a menor das disponibilidades do componente dependente.

Isso pode ser ilustrado com o exemplo apresentado na tabela a seguir (os números aqui são amostras, mas muito realistas):

Componente da dependência crítica	Probabilidade de falha	Valor da disponibilidade
Servidor da caixa de correio e armazenamento	5%	95%
Servidor de Acesso do Cliente	1%	99%
Rede	0,5%	99,5%
Potência	0,1%	99,9%
Serviço geral (depende de todos os componentes acima)	6,51383%	95% x 99% x 99,5% x 99,9% = 93,48617%

Nesse exemplo, você pode ver como as dependências de serviço são criticamente importantes. Mesmo para um banco de dados da caixa de correio que nunca falha (nunca é corrompida, nunca é infectada por vírus, etc.), a disponibilidade ainda permanece abaixo de 93,5%!

Conclusão: muitas dependências de serviço reduzem a disponibilidade.

Tudo o que você pode fazer para reduzir o número ou o impacto das dependências do serviço causará impacto positivo na disponibilidade geral do serviço. Por exemplo, você pode melhorar a maturidade operacional simplificando e protegendo o gerenciamento do servidor e otimizando os procedimentos operacionais. No lado técnico, você pode tentar reduzir o número de dependências do serviço tornando seu design mais simples – por exemplo, eliminando design complexo baseado em SAN, incluindo cartões HBA, comutadores de fibra, controladores de matriz e até mesmo controladores RAID e substituindo-o por um design DAS simples com um mínimo de peças móveis.

A redução nas dependências do serviço sozinha pode não ser suficiente para trazer a disponibilidade para o nível desejado. Outra maneira muito eficiente para aumentar a disponibilidade resultante e minimizar o impacto das dependência de serviço é aproveitar vários métodos de redundância, como utilizar fontes de alimentação duplas, placas de rede unidas, servidores de conexão em comutadores de rede múltiplos, usando a proteção RAID do sistema operacional, implementar balanceadores de carga para servidores de Acesso do Cliente e várias cópias dos bancos de dados da caixa de correio. Mas como exatamente a redundância aumenta a disponibilidade? Vamos olhar mais atentamente o balanceamento de carga e várias cópias do banco de dados como exemplo importantes.

Como a redundância causa impacto na disponibilidade

Conceitualmente, todos os métodos de redundância significam uma coisa: há mais de uma instância de componentes disponível e pode ser usado simultaneamente com outras instâncias (como no balanceamento de carga) ou como uma substituição (como nas várias cópias do banco de dados). Vamos supor que temos n instâncias de um determinado componente (n servidores em uma matriz CAS ou n cópias do banco de dados em um DAG). mesmo se um deles falhar, as outras instâncias ainda podem ser usadas, mantendo assim a disponibilidade. A única situação quando enfrentamos inatividade real é quando todas as instâncias falham.

Conforme definido anteriormente, a probabilidade de falha para qualquer instância fornecida é P = 1 – A. Todas as instâncias são estatisticamente independentes umas das outras, o que significa que a disponibilidade ou falha de qualquer uma delas não causa impacto na disponibilidade de outras instâncias. Por exemplo, a falha de uma determinada cópia do banco de dados não causa impacto na probabilidade de falha de outra cópia daquele banco de dados (uma possível advertência aqui pode ser a corrupção do banco de dados lógico propagando da primeira cópia do banco de dados danificado para todas as outras cópias, mas vamos ignorar isso fator altamente improvável por enquanto – afinal, você sempre pode implementar uma cópia defasada do banco de dados ou um backup tradicional do ponto no tempo para tratar disso).

Novamente usando o mesmo teorema da teoria da probabilidade, a probabilidade de ralha de um conjunto de n componentes independentes é um produto das probabilidades de cada componente. Como todos os componentes aqui são idênticos (instâncias diferentes do mesmo objeto), o produto torna-se uma potência:

Aparentemente, pois P < 1, Pⁿ é inferior a P, o que significa que a probabilidade de falha reduz e como consequência a disponibilidade aumenta:

Para esclarecer, vamos considerar alguns exemplos da vida real. Digamos que estamos implementando várias cópias do banco de dados da caixa de correio, cada cópia é hospedada em uma única unidade SATA. Estatisticamente, a taxa de falha das unidades SATA é ~5% em um ano[1], que nos dá 5% de probabilidade de falha: P = 0,05 (que significa disponibilidade de 95%: A = 0,95). Como a disponibilidade mudará conforme adicionamos mais cópias do banco de dados? Olhe a tabela a seguir que deve ser autoexplicativa:

Número de cópias do banco de dados	Probabilidade de falha	Valor da disponibilidade
1	P₁ = P = 5%	A₁ = 1 – P₁ = 95%
2	P₂ = P² = 0,25%	A₂ = 1 – P₂ = 99,75%
3	P₃ = P³ = 0,0125%	A₃ = 1 – P₃ = 99,9875%
4	P₄ = P⁴ = 0,000625%	A₄ = 1 – P₄ = 99,9994%

Muito impressionante, não é? Basicamente, cada cópia adicional do banco de dados na unidade SATA introduz o fator de multiplicação de 5% ou 1/20, assim a probabilidade de falha torna-se 20 vezes menor com cada cópia (e, de modo correspondente, a disponibilidade aumenta). Você pode ver que mesmo com as unidades SATA mais suspeitas implementar apenas 4 cópias do banco de dados trás disponibilidade do banco de dados para cinco noves.

Isso já é muito bom, mas pode ficar ainda melhor? Posso aumentar a disponibilidade ainda mais mesmo fazendo alterações na arquitetura (por exemplo, se adicionar ainda outra cópia do banco de dados estiverfora de questão)?

Realmente, é possível. Se você melhorar a disponibilidade individual de qualquer componente de dependência, isso será fator de aumento na disponibilidade geral do serviço, e leva a um efeito muito mais forte de adicionar componentes redundantes. Por exemplo, uma maneira possível para fazer isso sem quebrar a banca é usar unidades Nearline SAS em vez de unidades SATA. As unidades SAS têm uma taxa de falha anual de ~2,75% em vez dos ~5% da SATA. Isso reduzirá a probabilidade de falha para o componente de armazenamento no cálculo acima e, por isso, aumenta a disponibilidade geral do serviço. Basta comparar o impacto da adição de várias cópias do banco de dados:

5% AFR = fator de multiplicação 1/20 = cada nova cópia torna a falha do banco de dados 20 vezes menos provável.
2,75% AFR = fator de multiplicação de 1/36 = cada nova cópia torna a falha do banco de dados 36 vezes menos provável.

Esse impacto significativo que as cópias adicionais do banco de dados têm na disponibilidade do banco de dados também explica nossa orientação em como utilizar a proteção de dados nativos do Exchange que diz que várias cópias do banco de dados podem ser substituídas por backups tradicionais se um número suficiente (três ou mais) de cópias do banco de dados for implementado.

A mesma lógica se aplica à implementação de vários servidores de acesso para clliente em uma matriz CAS, vários comutadores de rede, etc. Vamos supor que implementamos 4 cópias do banco de dados e 4 servidores de Acesso do Cliente, e vamos revisitar a tabela de disponibilidade do componente que analisamos anteriormente:

Componente da dependência crítica	Probabilidade de falha	Valor da disponibilidade
Servidor de caixa de correio e armazenamento (4 cópias)	5% ^ 4 = 0,000625%	99,999375%
Servidor de Acesso do Cliente (4 servidores, instalados separadamente)	1% ^ 4 = 0,000001%	99,999999%
Rede	0,5%	99,5%
Potência	0,1%	99,9%
Serviço geral (depende de todos os componentes acima)	0,6%	99,399878%

Você pode ver como apenas porque implantamos 4 servidores de Acesso do Cliente e 4 cópias do banco de dados, a probabilidade de falha do serviço geral diminuiu mais do que 10-fold (de 6,5% a 0,6%) e disponibilidade do serviço aumenta de forma correspondente de 93,5% para um valor muito mais aceitável de 99,4%!

Conclusão: adicionar redundância às dependências do serviço aumenta a disponibilidade.

Juntando as peças

Uma questão interessante surge das conclusões anteriores. Analisamos dois fatores diferentes que causam impacto na disponibilidade geral do serviço de duas maneiras diferentes e descobrimos duas conclusões claras:

adicionar mais dependências do sistema reduz a disponibilidade
adicionar redundância às dependências do sistema aumenta a disponibilidade

O que acontece se os ambos forem fatores de uma determinada solução? Qual tendência é mais forte?

Considere o seguinte cenário:

Implementamos dois servidores de caixa de correio em um DAG com duas cópias do banco de dados da caixa de correio (uma cópia em cada servidor) e implementamos dois servidores de Acesso do Cliente em uma matriz com carga balanceada. (Para simplificar, só consideraremos a disponibilidade de um banco de dados da caixa de correio para conexões do cliente, deixando o Transporte de Hub e a Unificação de Mensagens fora de consideração por enquanto). Supondo que cada servidor tem sua probabilidade de falha individual de P, a disponibilidade desse sistema será melhor ou pior do que a disponibilidade de um único servidor autônomo do Exchange com funções de servidor de Caixa de Correio e Acesso do Cliente implementadas?

No primeiro cenário, os servidores de Caixa de Correio são independentes e ficarão indisponíveis somente se ambos os servidores falharem. A probabilidade de falha para o conjunto de dois servidores da caixa de correio será P × P = P². De modo correspondente, sua disponibilidade será A_MBX = 1 – P². Seguindo a mesma lógica, o serviços CAS estarão indisponíveis somente se ambos os servidores de Acesso do Cliente falharem, assim a probabilidade de falha para o conjunto de dois servidores de Acesso do Cliente serão novamente P × P = P², e de modo correspondente, sua disponibilidade será A_CAS = 1 – P².

Nesse caso, conforme você pode imaginar, dois servidores de caixa de correio ou dois servidores de Acesso do Cliente são exemplos de componentes redundantes do sistema.

Continuando com esse cenário… Para o sistema inteiro estar disponível, os dois conjuntos de servidores (conjunto de servidores de caixa de correio e Acesso do Cliente) devem estar disponíveis simultaneamente. Não falharem simultaneamente, mas estarem disponíveis simultaneamente, porque agora eles representam dependências do sistema em vez de componentes redundantes. Isso significa que a disponibilidade geral do serviço é um produto de disponibilidades de cada conjunto:

Certamente, o segundo cenário é muito mais simples, pois há apenas um servidor para considerar e sua disponibilidade é simples A = 1 – P.

Então, agora que calculamos os valores da disponibilidade para ambos os cenários, qual valor é maior, (1-P²)² ou 1-P?

Se marcarmos os gráficos de ambas as funções, veremos o seguinte comportamento:

(Eu usei o mecanismo computacional grátis Wolfram Alpha Mathematica Online para marcar de maneira rápida e fácil).

Podemos ver isso para os valores pequenos de P, a disponibilidade do sistema complexo de quatro servidores é maior que a disponibilidade do servidor único. Não há surpresa; isso é o que esperamos, certo? Entretanto, em P ~ 0.618 (mais precisamente, 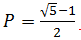) os dois marcadores cruzam e para valores maiores de P o sistema de servidor único realmente tem maior disponibilidade. Claro que você esperaria que o valor de P estivesse muito próximo a zero na vida real; entretanto, se você estiver planejando criar sua solução a partir de componentes muito suspeitos, provavelmente seria melhor com um único servidor.

Impacto da falha de domínios

Infelizmente, cenários de implementação da vida real raramente são tão simples quanto as situações discutidas acima. Por exemplo, como alterar a disponibilidade do serviço se você implementar servidores multifunção? Observamos no cenário acima que combinando as funções do servidor reduz efetivamente o número de dependências do serviço, então, provavelmente seria uma coisa boa? O que acontece se você colocar duas cópias do banco de dados do mesmo banco de dados na mesma matriz SAN ou invólucro DAS? O que acontece se todos os seus servidores de caixa postal estiverem conectados ao mesmo comutador de rede? O que acontece se você tiver todos acima e mais?

Todas essas situações lidam com o conceito de falha de domínios. Nos exemplos acima, o hardware do servidor ou uma matriz SAN, ou um comutador de rede representam uma falha do domínio. A falha do domínio interrompe a independência ou redundância dos componentes que ele combina – por exemplo, a falha do hardware do servidor em um servidor multifunção significa que todas as funções do Exchange nesse servidor ficam indisponíveis; de modo correspondente, a falha de um invólucro de disco ou de uma matriz SAN significa que todas as cópias do banco de dados hospedadas nesse invólucro ou matriz fica indisponível.

As falhas de domínio não são necessariamente uma coisa ruim. A diferença importante é que tipo de componentes constituem uma falha de domínio – são diferentes dependências do sistema ou componente redundantes do sistema. Vamos considerar dois exemplos acima para compreender essa diferença.

Cenário do servidor multifunção

Vamos comparar a disponibilidade de dois sistemas diferentes:

As funções dos servidores de caixa de correio e de Acesso do cliente hospedados no mesmo servidor que tem a probabilidade de falha de hardware de P;
As mesmas funções hospedadas em dois servidores separados, cada um com a mesma probabilidade de falha de hardware;

No primeiro caso, o hardware de um servidor único representa uma falha de domínio. Isso significa que todas as funções hospedadas estão todas disponíveis ou indisponíveis. Isso é simples; a disponibilidade geral desse sistema é A = 1 – P.

No segundo caso, o serviço geral estará disponível somente quando ambos os servidores estiverem disponíveis independentemente (porque cada função representa uma dependência crítica). Por isso, baseado na teoria da probabilidade, sua disponibilidade será A × A = A².

Novamente, como A < 1, isso significa que A² < A, então, a disponibilidade no segundo caso será menor.

Aparentemente, podemos adicionar outras funções do servidor do Exchange (Transporte de Hub e Unificação de Mensagens, se necessário) para o mesmo cenário sem interromper essa lógica.

Conclusão: a colocação das funções do servidor do Exchange em um servidor multifunção aumenta a disponibilidade geral do serviço.

Cenário de armazenamento compartilhado

Agora vamos considerar outro cenário de falha de domínio (duas cópias de banco de dados compartilhando a mesma matriz de armazenamento) e compara a disponibilidade do banco de dados nos dois casos a seguir:

Duas cópias do banco de dados hospedadas no mesmo armazenamento compartilhado (matriz SAN ou invólucro DAS), que tem a probabilidade de falha de P;
As mesmas cópias do banco de dados hospedadas em dois sistemas de armazenamento separados, cada um com a mesma probabilidade de falha;

No primeiro caso, o armazenamento compartilhado representa uma falha do domínio. Como no cenário anterior, isso significa que ambas as cópias do banco de dados estão disponíveis ou indisponíveis simultaneamente, então a disponibilidade geral é novamente A = 1 – P.

No segundo caso, o serviço geral estará disponível se pelo menos um sistema estiver disponível, e indisponível somente se ambos os sistemas falharem. Os sistemas de armazenamento em questão são independentes, por isso, a probabilidade de falha do serviço geral é P × P = P² e de modo correspondente a disponibilidade geral do serviço é A = 1 – P².

Novamente, como P < 1, isso significa que P² < P e, por isso, 1 – P² > 1 – P. Isso significa que a disponibilidade no segundo caso é maior.

Conclusão: a colocação das cópias do banco de dados no mesmo sistema de armazenamento reduz a disponibilidade geral do serviço.

Então, qual é a diferença entre esses dois cenários, porque a introdução de uma falha de domínio aumenta a disponibilidade no primeiro caso e reduz a disponibilidade no segundo caso?

É porque a falha de domínio no primeiro caso combina dependências de serviço, reduzindo efetivamente seus números e melhorando a disponibilidade, enquanto a falha de domínio no segundo caso combina componentes redundantes, reduzindo efetivamente a redundância e prejudicando a disponibilidade.

Todos esses conceitos e conclusões provavelmente seriam visualizados como segue:

(Não, nós não usamos o Wolfram Alpha para desenhar esse gráfico!)

Resumo

A arquitetura do Exchange 2010 oferece possibilidades poderosas para adicionar redundância no nível do Exchange (como implantação de várias cópias do banco de dados ou vários servidores de Acesso do Cliente em uma matriz CAS) e para reduzir o número de dependências do sistema (combinando funções do servidor do Exchange em um servidor multifunção ou usando arquitetura de armazenamento mais simples sem um número excessivo de componentes críticos). A regras e fórmulas simples apresentadas nesse artigo permitem calcular o efeito no valor da disponibilidade da implantação das cópias do banco de dados ou da combinação de funções do servidor do Exchange; você também pode calcular o impacto de falhas do domínio. É importante observar que tentamos usar esses modelos matemáticos simples para ilustrar os conceitos, não fingir para obter os valores precisos da disponibilidade. A vida real raramente apresenta os cenários básicos simples e você precisa de cálculos muito mais complexos para obter estimativas razoáveis para a disponibilidade dos seus sistemas reais; pode ser mais fácil para simplesmente medir a disponibilidade estatisticamente e verificar e ela atende aos requisitos SLA. Entretanto, a compreensão dos fatores que causam impacto na disponibilidade e como eles funcionam juntos em uma solução de engenharia complexa deve ajudar a projetar a solução de maneira adequada e obter um aumento significativo na disponibilidade geral do serviço, atendendo até mesmo os requisitos comerciais mais exigentes.

Boris Lokhvitsky
Arquiteto de entrega

[1] Os seguintes estudos realizados pela Carnegie Mellon University, pelo Google e pela Microsoft Research mostram 5% AFR para unidades SATA:

https://www.usenix.org/events/fast07/tech/schroeder/schroeder.pdf

https://labs.google.com/papers/disk_failures.pdf

https://research.microsoft.com/research/pubs/view.aspx?msr_tr_id=MSR-TR-2005-166