Little's Law and How It Impacts Load Testers
Load testing is all about queuing, and servicing the queues. The main goals in our tests are parts of the formula itself. For Example: the response times for a test is equivalent to service times of a queue, load balancing with multiple servers is the same as queue concurrency. Even when we look at how we are designing a test we see relationships to this simple theory.
I will walk you through a few examples and hopefully open up this idea for you to use in amazing ways.
How to determine concurrency during a load test? (Customer Question: What was the average number of concurrent requests during the test? What about for each server?)
Little's Law -> Adjusted to fit load testing terminology
L = λW
L is the average concurrency
λ is the request rate
W is the Average Response Time
For Example: We have a test that ran for 1 hour, the average response times were 1.2 seconds. The average number of requests sent to the server by the test per second was 16.
L = 16 * 1.2
L = 19.2
Average number of concurrent request processing on the servers was 19.2 averaged per second.
Let’s say we have perfect load balancing, of 5 servers.
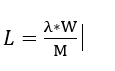 M = Number of Servers/Nodes
M = Number of Servers/Nodes
L = Concurrent requests per Server/Node .
L= 19.2/5
So, each server is processing ~3.84 concurrent requests per second on average
This explains why, when we reach our maximum concurrency on a single process, response times begin to grow and throughput levels off. Thus, we need to optimize the service times, or increase the concurrency of processing. This can be achieved by either scaling out or up depending on how the application is architected.
Also, this is not all entirely true, there will be time spent in different parts of the system, some of which have little to no concurrency, two bits cannot exist concurrently on the same wire electrically, as of writing this article.
Can we achieve the scenario objectives given a known average response time hypothesis?
For tests that use “per user per hour pacing”, we can determine the minimum number of users necessary to achieve the target load given a known average response time under light load. You can obtain the average response times from previous tests or you can run a smoke test with light load to get it.
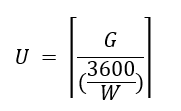
3600 seconds in an hour
W = Average Response Times in seconds for the test case you are calculating
Number of users needed U = 3600/W
G = Throughput Goal (Transactions per hour)
Let’s say we have a average response time of 3.6 seconds, and our goal is to run this test case 2600 times per hour. What would be the minimum number of users to achieve this?
U = ceil(2600/(3600/3.6))
U=3
Pacing = G / U
Pacing = 866
So, the scenario would be 3 users and the test case would be set to execute 866 times per user per hour. Personally, I like to add 20% additional users to account for response time growth just in case the system slows down. For example: I would run with 4 vUsers at 650 Tests per User per Hour, or 5 vUsers at 520 Tests per User per Hour.
There are endless possibilities to using this formula to understand and predict behavior of the system, post some examples of how you would use queueing theory in the comment section below.
Have a great day and happy testing!
Comments
- Anonymous
October 04, 2017
Nice examples. This great information for performance testers trying to define concurrency and workload scenarios for load tests. - Anonymous
November 07, 2017
Good one. But, shouldn't the 'Pacing' calculation be 'G / U'? Hope this is a typo.- Anonymous
November 08, 2017
Yes, it was a typo; good catch. I have updated it.
- Anonymous