Algoritmos y esquema de perfil del modelo de mapa de gama de WCS
- Información general
- Arquitectura del perfil de modelo de mapa de gamut
- Generación del límite de gama
- Esquema GMMP
- Elementos de esquema GMMP
- GamutMapModel
- Algoritmos de línea base de GMMP
- Alineación de los ejes neutros
-
Descripción de los límites de gamut y algoritmos de shell de gamut
- Triangulación del límite de gama
- Elementos de línea de límite
- Operación de gamut: CheckGamut
- Plano de Hue completo: Intersección
- Operación de gamut: CheckGamut (continuación)
- Asignación de gama mínima de diferencia de color
- Suavizado de matiz
- Establecer elementos primarios y secundarios en la descripción del límite de gama
- Establecer el eje neutro en la descripción del límite de gama
- Temas relacionados
Información general
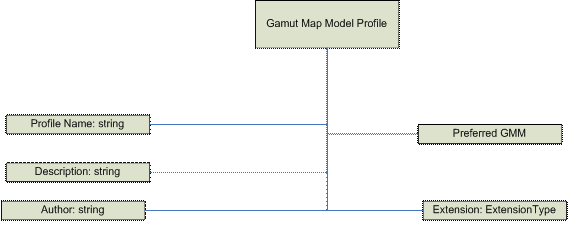
Este esquema se usa para especificar el contenido de un perfil de modelo de mapa de gama (GMMP). Los algoritmos de línea base asociados se describen en el tema siguiente.
El esquema GMMP básico consta de información de encabezado común, una referencia opcional a un complemento de modelo de mapa de gamut preferido y etiquetas de extensión.
Además, GMMP proporciona información explícita sobre el modelo de mapa de gamut de destino y proporciona una directiva en el modelo de mapa de gamut de reserva de línea base para usarlo si el modelo de destino no está disponible. El esquema puede incluir información de extensión privada, pero no incluirá ninguna otra información extraña.
Arquitectura del perfil de modelo de mapa de gamut
El muestreo del espacio de colorante del dispositivo de salida se realiza iterando a través de los colores de 0,0 a 1,0 con un paso fraccionario, acumulando todas las combinaciones de cada colorante en cada paso y, a continuación, conviértalos del espacio de color del dispositivo al espacio de apariencia de color mediante el método DM::D eviceToColorimetricColors seguido del método CAM::ColorimetricToAppearanceColors. A continuación se muestra un ejemplo de cómo se hace esto para RGB.
For (red= 0.0; red <= 1.0; red += redStep) {
For (green = 0.0; green <= 1.0; green += greenStep) {
For (blue = 0.0; blue <= 1.0; blue += blueStep) {
Colorants[0] = red; colorants[1] = green; colorants[2] = blue;
pRGBDM->DeviceToColorimetricColors(1, colorants, &XYZ);
pCAM->ColorimetricToAppearanceColors(1, &XYZ, &JCh);
}
}
}
Generación del límite de gama
Hay tres componentes para el límite de la gama: las principales, las muestras neutras y los shells. Las principales se generan tomando las principales del dispositivo y aplicando la transformación DeviceToColorimetric/ColorimetricToAppearance. Las muestras neutras se generan mediante el muestreo del espacio de coloración del dispositivo en el área neutra y la aplicación de la misma transformación. En el caso de tres dispositivos coloreados (RGB o CMY), las muestras neutras se definen como tener todos los colores iguales, por ejemplo, R == G == B. Para CMYK, las muestras neutras se definen como con C == M == Y == 0.
Los factores que influyen en los datos usados para crear el límite de la gama son las muestras de datos (solo dispositivos de línea base) y las condiciones de visualización. El tamaño del paso que se usa para realizar el muestreo completo del espacio de colorant (para monitores y para shells probables) es una constante interna y no está disponible para la manipulación externa. El cambio de las condiciones de visualización cambia el comportamiento del modelo de apariencia de color (CAM) y modifica la forma del límite de la gama, por lo que debe generar un límite de gama vinculado al perfil de condiciones de visualización. Si se usan datos de ejemplo, como en el caso de impresoras de línea base y dispositivos de captura, las muestras tendrán un gran impacto en la forma de la gama de referencia y afectarán al comportamiento del propio modelo.
En el caso de los dispositivos de entrada, como cámaras y escáneres, se usan diferentes muestreos para generar el shell de referencia y el shell factible. El shell de referencia se genera a partir de las medidas usadas para inicializar el modelo de dispositivo. El shell factible se genera de forma similar a la ilustración anterior para los dispositivos de salida. La diferencia es que cuando se introduce un destino típico, no se obtienen valores totalmente saturados (donde R, G o B = 255). Debe extrapolar mediante el modelo de dispositivo para calcular esos valores.
Esquema GMMP
<?xml version="1.0" encoding="UTF-8"?>
<xs:schema
xmlns:gmm="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"
xmlns:wcs="http://schemas.microsoft.com/windows/2005/02/color/WcsCommonProfileTypes"
targetNamespace="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"
xmlns:xs="http://www.w3.org/2001/XMLSchema"
elementFormDefault="qualified"
attributeFormDefault="unqualified"
blockDefault="#all"
version="1.0">
<xs:annotation>
<xs:documentation>
Gamut Map Model profile schema.
Copyright (C) Microsoft. All rights reserved.
</xs:documentation>
</xs:annotation>
<xs:import namespace="http://schemas.microsoft.com/windows/2005/02/color/WcsCommonProfileTypes" />
<xs:element name="GamutMapModel">
<xs:complexType>
<xs:sequence>
<xs:element name="ProfileName" type="wcs:MultiLocalizedTextType"/>
<xs:element name="Description" type="wcs:MultiLocalizedTextType" minOccurs="0"/>
<xs:element name="Author" type="wcs:MultiLocalizedTextType" minOccurs="0"/>
<xs:element name="DefaultBaselineGamutMapModel">
<xs:simpleType>
<xs:restriction base="xs:string">
<xs:enumeration value="HPMinCD_Absolute"/>
<xs:enumeration value="HPMinCD_Relative"/>
<xs:enumeration value="SGCK"/>
<xs:enumeration value="HueMap"/>
</xs:restriction>
</xs:simpleType>
</xs:element>
<xs:element name="PlugInGamutMapModel" minOccurs="0">
<xs:complexType>
<xs:sequence>
<xs:any namespace="##other" processContents="skip"
minOccurs="0" maxOccurs="unbounded" />
</xs:sequence>
<xs:attribute name="GUID" type="wcs:GUIDType" use="required"/>
</xs:complexType>
</xs:element>
</xs:sequence>
<xs:attribute name="ID" type="xs:string" use="optional" />
</xs:complexType>
</xs:element>
</xs:schema>
Elementos de esquema GMMP
GamutMapModel
Este elemento es una secuencia de los siguientes subelementos:
- Cadena ProfileName,
- DefaultBaselineGamutMapModel,
- Cadena de descripción opcional,
- Cadena de autor opcional,
- PlugInGamutMap opcional y
- ExtensionType opcional.
Condiciones de validación : cada sub-elemento se valida por su propio tipo.
Espacio de nombres
xmlns:gmm="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"
targetNamespace="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"
Versión
Versión "1.0" con la primera versión de Windows Vista.
Condiciones de validación : 1.0 en Windows Vista. Las versiones <2.0 también son válidas para admitir cambios no importantes en el formato.
Documentación
Esquema de perfil de modelo de mapa de gamut.
Copyright (C) Microsoft. Todos los derechos reservados.
Condiciones de validación : cada sub-elemento se valida por su propio tipo.
Tipo DefaultBaselineGamutMapModel
Tipo UINT
Valores de enumeración:
- "MinCD\_Absolute" "MinCD\_Relative" "SIG\_KNEE" "HueMap"
Condiciones de validación : los valores deben coincidir con una de las enumeraciones anteriores.
PlugInGamutMapType
Este elemento es una secuencia de un GUID GuidType y cualquier sub elementos.
Condiciones de validación : el GUID se usa para coincidir con el GUID de dll de PlugIn de GMM. Hay un máximo de 100 000 subelementos personalizados.
ExtensionType
Este elemento es una secuencia opcional de cualquier subproceso.
Condiciones de validación : puede haber un máximo de 100 000 subelementos.
Algoritmos de línea base de GMMP
Alineación de los ejes neutros
La mayoría de los algoritmos de asignación de gama tienen un objetivo de asignar el eje neutro del dispositivo de origen al eje neutro del dispositivo de destino: es decir, el blanco va a blanco, negro a negro y gris a gris. Esto se aborda en parte mediante el escalado de la ligereza de los colores de origen para que coincida con el intervalo de iluminación del dispositivo de destino. Pero eso no soluciona completamente el problema.
Es una propiedad física de la mayoría de los dispositivos de imagen que la cromática del dispositivo blanco no coincide exactamente con la cromática del dispositivo negro. Por ejemplo, el monitor blanco depende de la suma de las cromáticas y las luminancias relativas de los tres principales, mientras que el monitor negro depende de la reflectancia de la superficie de visualización. El blanco de la impresora depende de la cromática del papel, mientras que el negro de la impresora depende de la tinta o el tóner utilizado. Un modelo de apariencia que asigna el blanco del dispositivo exactamente al eje neutro del espacio de apariencia (cromática exactamente igual a cero) no asignará el dispositivo negro al eje neutro. Dado que el ojo es más sensible a las diferencias cromáticas a medida que aumenta la ligereza, los grises medios se representarán como aún más cromáticos que el negro del dispositivo. (En la figura 1 se muestra la curvatura de los ejes neutros en dos dimensiones. De hecho, los ejes neutros forman una curva más compleja en tres dimensiones).
Aunque la CAM predice que estos colores neutros del dispositivo aparecerán cromáticos, los observadores reales parecen compensarlo. La mayoría de las personas no consideran que estos valores neutros del dispositivo sean cromáticos. Para la mayoría de los modelos de asignación de gamut, por lo tanto, debe seguir asignando neutrales de origen a neutrales del dispositivo.
Para asignar neutrales de origen a neutrales del dispositivo, ajuste los límites de la gama de origen y destino y cada píxel al aplicar el algoritmo de asignación de gama. En primer lugar, ajuste cada valor en el color de origen para que el eje neutro del dispositivo de origen en el color de origen caiga directamente en el eje neutro del espacio de apariencia. (Vea el lado izquierdo de la figura 1). A continuación, ajuste la descripción del límite de gama del dispositivo de destino para que cada color del eje neutro del dispositivo de destino en el color de límite de gama del dispositivo de destino caiga directamente en el eje neutro del espacio de apariencia. (Vea el lado derecho de la figura 1).
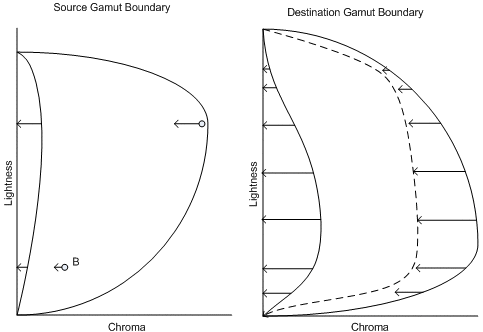
Figura 1 : Alineación de los ejes neutros ilustrados. Izquierda: ajuste los puntos de origen en relación con el eje neutro del dispositivo de origen. Derecha: ajuste la descripción del límite de la gama de destino en relación con la descripción del límite de la gama de destino.
Tenga en cuenta que ajusta cada valor de píxel de origen en relación con el eje neutro en ese valor de ligereza. Esto garantiza que los neutrales del dispositivo de origen caigan en el eje neutro del modelo de apariencia. También se desplazan todos los demás colores en esa ligereza por la misma cantidad, de modo que no haya discontinuidades en la representación de la gama de origen. Tienes que cambiar por diferentes cantidades en diferentes niveles de ligereza, ya que los neutrales del dispositivo de origen no se representan como iguales cromáticos en los diferentes niveles de ligereza. Claramente, esto no es una transformación trivial.
Controlar los valores del dispositivo de destino es un poco más complicado. Inicialmente, ajusta todo el límite de la gama de destino de forma similar, pero en relación con el eje neutro del dispositivo de destino. Esto se ilustra en la figura 1 del lado derecho. Ese ajuste garantiza que los valores grises de origen se asignarán a los valores grises de destino. Este es el espacio en el que funcionan los algoritmos de asignación de gama.
Sin embargo, este espacio no describe con precisión el verdadero comportamiento del dispositivo de destino. Debe invertir la asignación antes de que se entreguen los colores asignados a la gama al modelo de apariencia y al modelo de dispositivo de destino. Se desplazan todos los valores asignados por lo contrario del desplazamiento aplicado anteriormente al eje neutro del dispositivo de destino. Esto asigna el eje neutro de destino al valor representado originalmente por la CAM. Hace lo mismo para el límite de gama y todos los valores intermedios.
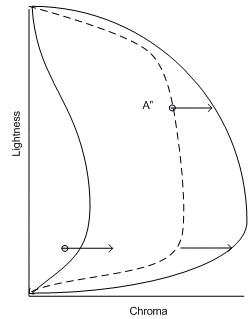
Figura 2 : Deshacer la alineación del eje neutro del dispositivo de destino
Diferencia mínima de color (MinCD)
Mínima diferencia de color (MinCD) Versiones relativas y absolutas, equivalentes a la intención colorimétrica ICC.
Nota
MinCD GMM es adecuado para asignar gráficos y arte de línea que contiene colores de "logotipo" (colores puntuales), degradados de color del logotipo con algunos colores de gama fuera de gama y para la fase final de transformaciones de corrección. Aunque el MinCD GMM podría usarse para imágenes fotográficas que están completamente dentro de la gama de destino, no se recomienda para la representación general de imágenes fotográficas. La asignación de colores fuera de gama a colores en la superficie de la gama de destino puede dar lugar a artefactos no deseados, como las irregularidades de tono o cromática en degradados suaves que cruzan el límite de la gama. BasicPhoto se recomienda para imágenes fotográficas. Si una imagen fotográfica o contona requiere una asignación de gama distinta de BasicPhoto, la alternativa debe ser crear un complemento GMM que implemente esa asignación, en lugar de usar MinCD.
Los colores de la gama se dejan sin cambios. Para los colores fuera de la gama, la luz y el cromático se ajustan al encontrar el punto en la gama de destino que tiene la distancia de color mínima desde los puntos de entrada fuera de la gama. La distancia de color se calcula en el espacio JCh. Sin embargo, se pondera la distancia en ligereza (J) y la distancia en cromática (C) o matiz (h) de forma diferente. Una función de peso dependiente del cromático se utiliza para la distancia en ligereza de modo que el peso sea más pequeño para el cromático pequeño y mayor para un gran cromático hasta que se alcance un cromático de umbral, después del cual el peso permanece en 1, es decir, el mismo peso que la distancia en cromática o matiz. Esto sigue el uso recomendado para CMC y CIEDE2000. Hay dos variantes: colorimétrica relativa y colorimétrica absoluta.
Colorimétrica relativa: En primer lugar, alinee los ejes neutros de origen y destino, como se ha descrito anteriormente. A continuación, recorte el color de origen ajustado al límite de gama de destino ajustado. (Vea la figura 4. Asignación cromática a lo largo de la ligereza constante). Reajuste los valores del dispositivo de destino como se ha descrito anteriormente. En el caso de un límite de gama de destino monocromático, el recorte cromático significa que el valor cromático (C) se establece en cero (0,0).
Colorimétrica absoluta: Esto es similar a la colorimétrica relativa, pero sin la alineación del eje neutro de origen y destino. El valor de origen se recorta directamente en el eje neutro de destino. Tenga en cuenta que si los límites de la gama de origen y destino son monocromáticos, el comportamiento es idéntico a la variante colorimétrica relativa; es decir, se realiza la alineación de los ejes neutros y, a continuación, el cromático se recorta a cero. Esto garantiza que se alcance una salida razonable incluso si los medios y los colores son significativamente diferentes.
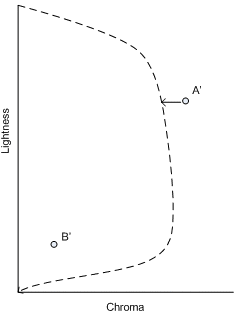
Figura 3 : Recorte de MinCD en la gama ajustada
BasicPhoto
Información general
BasicPhoto: equivalente a la intención preferida de ICC, pictorial o perceptual.
Este algoritmo es una variante de la asignación de ligereza sigmoidal dependiente del cromático y el escalado de rodilla cusp (SGCK) descrito por CIE TC8-03 en CIE156:2004. Este algoritmo variant admite descriptores de límites de gama (GBD) con shells de doble gama; es decir, GBD con un shell de referencia y un shell factible. El algoritmo SGCK, que asume originalmente solo un shell de gama en el GBD, se basa en el algoritmo de SIG_KNEE (Braun 1999), que incorpora la asignación de luz sigmoidal y el escalado de funciones de rodilla propuesto por Braun y Fairchild (1999), combinado con la dependencia cromática de GCUSP (Morovic, 1998). Mantiene constante de matiz percibido, por ejemplo, ángulo de matiz en jab corregido por matiz, y usa un escalado de ligereza sigmoidal genérico (independiente de la imagen) que se aplica de forma dependiente del cromático y un cromatizado de función de rodilla del 90 por ciento. La variante se escala a lo largo de líneas de ligereza constante.
El caso del shell de una sola gama
Resulta útil revisar el algoritmo en caso de que los GBD de origen y destino tengan solo un shell de gama. En este caso, el algoritmo consta de los siguientes cálculos.
En primer lugar, realice la asignación de ligereza inicial con la fórmula siguiente:
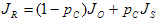 (1)
(1)
donde Jₒ es la ligereza original y JR es la luminosidad de reproducción.
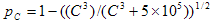 (2)
(2)
Cuando el límite de la gama de origen es monocromo, el valor cromático será cero para el límite monocromo debido a la alineación del eje neutro. Esto dará como resultado el caso degenerado en el que C es igual a cero. En este caso, pC se establece en 1.
pC es un factor de ponderación dependiente del cromático (Morovic, 1998) que depende del cromático del color original, C y JS son el resultado de la ligereza original que se asigna mediante una función sigmoidal.
Para calcular JS (Braun y Fairchild, 1999), una tabla de búsqueda unidimensional (LUT) entre los valores de ligereza original y de reproducción se configura primero sobre la base de una función normal acumulativa discreta (S).
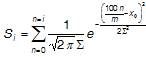 (3)
(3)
donde x ₀ y S son la media y desviación estándar de la distribución normal respectivamente e i = 0,1,2... m,m es el número de puntos utilizados en la LUT. Si es el valor de la función normal acumulativa para i /m por ciento. Los parámetros dependen de la ligereza del punto negro de la gama de reproducción y se pueden interpolar desde la tabla 1. Para obtener más información sobre cómo calcular estos parámetros, consulte Braun y Fairchild (1999, p. 391).
J minOut
5.0
10.0
15.0
20,0
x ₀
53.7
56.8
58.2
60.6
S
43,0
40,0
35,0
34,5
Tabla 1 : Cálculo básico del parámetro de compresión de la luzphoto
Para usar S como una Asignación de ligereza LUT (S LUT ), primero debe normalizarse en el intervalo de ligereza de [0,100]. A continuación, los datos normalizados se escalan en el intervalo dinámico del dispositivo de destino, como se muestra en ecuación 4, donde Jmin\ Out y Jmax\ Out son los valores de ligereza del punto negro y el punto blanco del medio de reproducción, respectivamente.
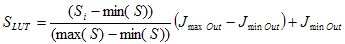 (4)
(4)
En este punto, los valores J S se pueden obtener del LUT interpolando entre los puntos m de los valores J O' y J S correspondientes que contiene y usando la siguiente ecuación como entrada.
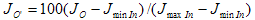 (5)
(5)
J minIn es el valor de ligereza del punto negro del medio original, J maxIn es el valor de ligereza del punto blanco del medio original y J O es la ligereza original. Para referencia posterior, puede indicar mediante S la función sigmoidal definida de la manera que se acaba de definir, como se muestra en la figura 4 siguiente.
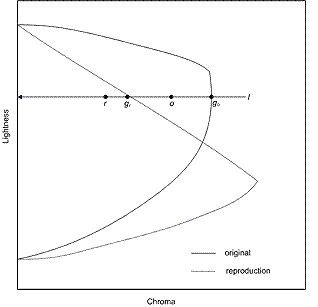
Figura 4 : Asignación de cromática a lo largo de la ligereza constante
En segundo lugar, si el límite de la gama de destino es cromático, comprima el cromático a lo largo de líneas de ligereza constante (l) y realice la compresión de la siguiente manera.
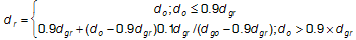 (6)
(6)
donde d representa la distancia desde E en l; g representa el límite de gama media; r representa la reproducción; y o la figura 5 original.
Figura 5 : Compresión cromática y ligera en BasicPhoto
Si el límite de la gama de destino es monocromático, el valor cromático se recorta en cero.
En tercer lugar, use un clip minCD (descrito anteriormente) para eliminar cualquier error residual.
Mejora en negro
El algoritmo anterior se puede modificar para mejorar el negro cuando el destino es un dispositivo de impresora. El problema tiene que ver con la elección de JminOut, que normalmente no corresponde al color más oscuro que puede producir una impresora.
Más concretamente, el color con mayor densidad, obtenido al colocar 100 por ciento tintas (o la cobertura máxima posible, si la limitación de GCR/tinta está en vigor), normalmente no es "neutral" en el espacio de apariencia de color. Vea la figura 6. En otras palabras, si se usa la ligereza mínima neutra para el dispositivo de destino, el escalador de ligereza construido se asignará a una ligereza mínima que no sea la densidad más alta que puede lograr la impresora. Considere el caso de uso adicional del monitor en la impresora. El monitor negro, R=G=B=0, se imprimirá como no la densidad más alta. El impacto en la calidad de la imagen es que falta profundidad y contraste.
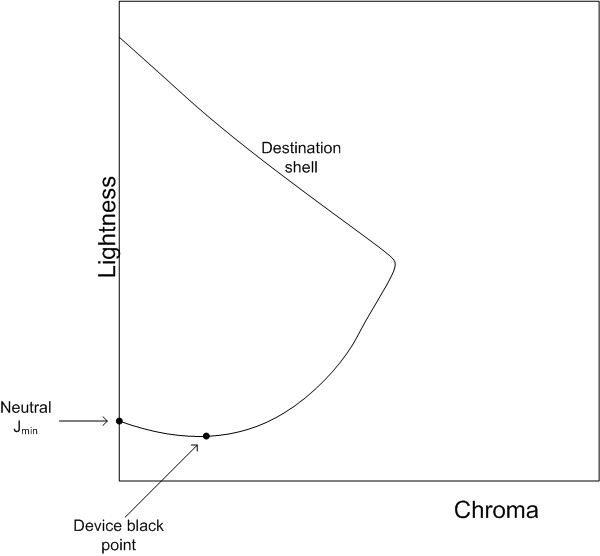
Figura 6 : El punto negro del dispositivo puede ser más oscuro que la ligereza mínima neutra.
Supongamos que el destino "punto negro del dispositivo" es Jkakbk/JkCkh k. Si C k no es cero, el punto negro del dispositivo no es neutro en relación con CAM02. Si utiliza J k para el destino "ligereza mínima neutra" en la construcción del escalador de ligereza; es decir, configuración
JminOut = Jk
y aplíquelo al shell de gama de origen, obtendrá la configuración que se muestra en la figura 7. En la figura, el plano de matiz corresponde a h k.
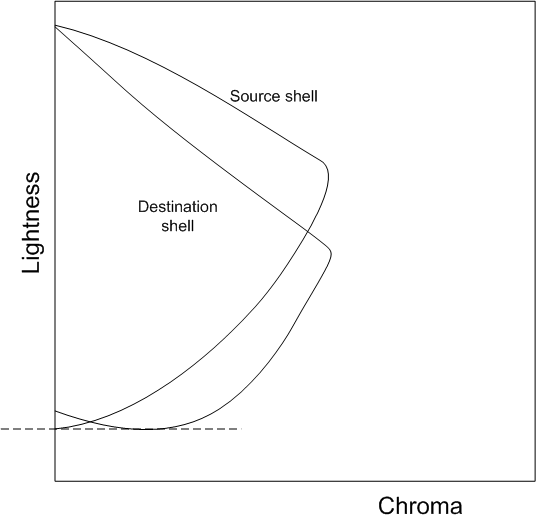
Figura 7 : Geometría mediante el escalador de luz modificado con el punto negro del dispositivo de destino
Para permitir que el algoritmo de compresión cromática subsiguiente continúe, desea alinear las ligerezas máximas y mínimas en los shells de origen y destino. Esto se puede lograr ajustando el shell de destino entre J neutralMin y J k cambiando los puntos a la izquierda. Además, esta transformación debe aplicarse en todo el espacio Jab, no solo en el plano de matiz correspondiente a h k.
La transformación es
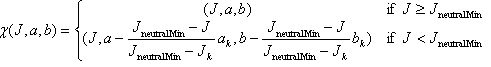
En la figura 8 se muestra el efecto de la transformación.
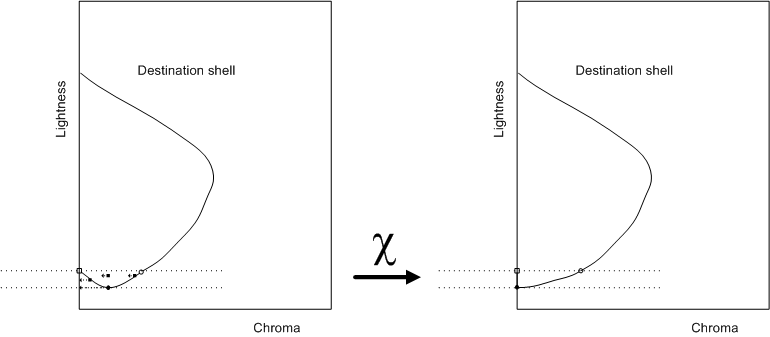
Figura 8 : Geometría mediante el escalador de luz modificado con el punto negro del dispositivo de destino
Después de aplicar el algoritmo de compresión cromática habitual, el punto debe ser "desplazado hacia atrás", es decir, la transformación inversa debe aplicarse para obtener el color asignado final.
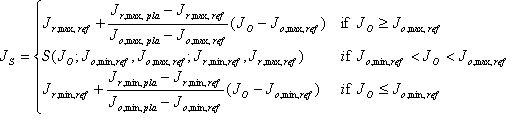
El caso de los shells de doble gama
El objetivo es generalizar SIG_KNEE para el shell de una sola gama en el caso en el que el GBD del dispositivo de origen o el GBD del dispositivo de destino tiene una estructura de dos shells. El shell interno se llamará el Shell de referencia, mientras que el shell externo se llamará Shell viable. Quiere tener en cuenta los siguientes casos.
(a) Tanto el GBD de origen como el GBD de destino tienen una estructura de dos shells.
(b) El GBD de origen tiene una estructura de dos shells; el GBD de destino solo tiene un shell.
(c) El GBD de origen solo tiene un shell; el GBD de destino tiene una estructura de dos shells.
(d) Tanto el GBD de origen como el GBD de destino tienen solo un shell.
El caso (d) es el caso del shell de una sola gama que se explicó anteriormente. En los casos (a), (b) y (c), puede generalizar el escalado de la ligereza para usar la información adicional de la estructura de doble shell. En los casos (b) y (c) en los que el origen o el destino solo tienen un shell, se introduce un "shell de referenciaducido" que se analizará en una sección posterior, "Shell de referenciaducida". El algoritmo general para dos shells se describirá para mayúsculas y minúsculas (a). Una vez que se explica la construcción del Shell de referenciaducida, el algoritmo también se puede aplicar a mayúsculas y minúsculas (b) y (c). En cuanto a la compresión cromática, la relación de compresión será determinada por las carcasas más grandes disponibles. En otras palabras, si el Shell Plausible y el Shell de Referencia están disponibles, se usará el Shell Plausible; De lo contrario, se usará el Shell de referencia.
Escalado generalizado de la ligereza
La existencia de dos shells para GBD de origen y destino significa que debe asignar un conjunto de cuatro puntos del GBD de origen a un conjunto correspondiente en el GBD de destino.
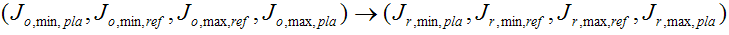
Los subíndices tienen los significados siguientes.
o o r: "original" (origen) o "reproducción" (destino)
min o max: ligereza neutra mínima o ligereza neutra máxima
pla o ref: Shell verosímil o Shell de referencia
La ordenación en cada cuádruple es también la magnitud relativa esperada de estos puntos.
El mapa reescalado de ligereza usa las dos primeras ecuaciones que el shell único, pero J S se define de una manera por partes como se indica a continuación.
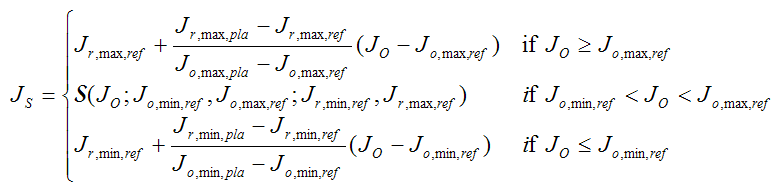 (7)
(7)
En otras palabras, es sigmoidal dentro del shell de referencia y lineal fuera. Vea la figura 9.
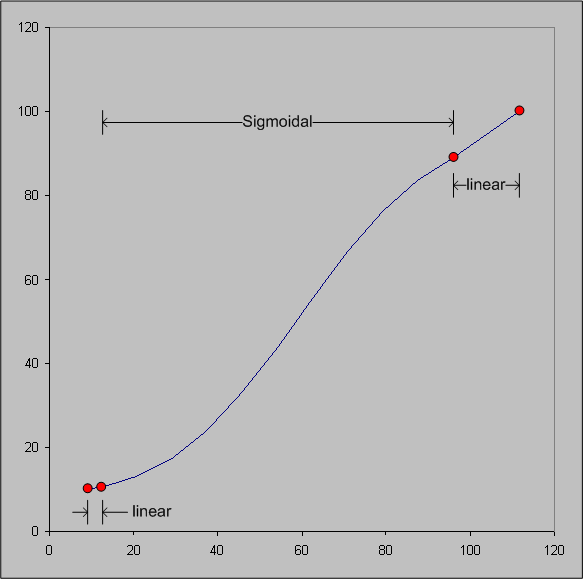
Figura 9 : Función de reescalamiento de ligereza para gbD de dos shells
SHELL DE REFERENCIADUCIDA
Cuando un GBD tiene un shell y el otro GBD tiene dos shells, debe crear un "Shell de referencia" para el GBD con solo un shell. El shell existente, que se llamaría Shell de referencia, se cambiará al "Shell plausible". De hecho, no tienes que crear un shell en el espacio de Jab completo. Dado que el escalado de ligereza solo usa J max y J min, solo tiene que componer estos valores para el Shell de referenciaducido. Hay dos casos, dependiendo de qué GBD tiene dos shells.
Caso 1: El GBD de origen tiene dos shells; destination GBD tiene un shell.
Determine el shell de referencias de destino inducido en el eje neutro; es decir, J r,\ min,\ ref y J r,\ max,\ ref del shell. Esto se hace mediante el siguiente algoritmo.
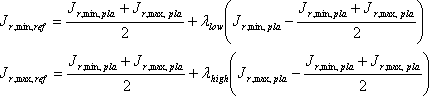
¿Los factores? bajo y ? de alto control la separación entre el Shell Plausible y el Shell de referencia. Un valor de 1 significa que los valores min de J o J mₐₓ valores coinciden. Sus valores se "deducen" del shell de referencia de origen y del shell viable de origen.
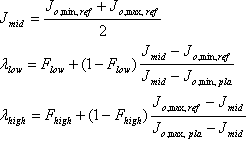
Los "factores de fudge" F bajo y F alto son parámetros ajustables que deben estar comprendidos entre 0 y 1. Si el valor es 0, el J min o J mₐₓ se deducen directamente de los shells de origen. En este caso, elija F low = 0,95 y F high = 0,1.
Caso 2: El GBD de origen tiene un shell; destination GBD tiene dos shells.
Determinar el shell de referencia de origen inducido en el eje neutro; es decir, J o,\ min,\ ref y J o,\ max,\ ref del shell. Esto se hace mediante el siguiente algoritmo.
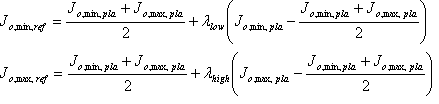
¿De nuevo, los factores ? bajo y ? control alto de la separación entre el Shell de Plausible y el Shell de referencia. Un valor de 1 significa que los valores min de J o J mₐₓ valores coinciden. Sus valores se "deducen" del shell de referencia de origen y del shell viable de origen:
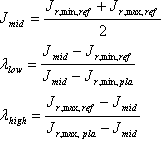
Motivos de los cambios de las recomendaciones de CIE TC8-03
BasicPhoto difiere de las recomendaciones de CIE TC8-03 de las siguientes maneras.
- El cromático no se comprime hacia la cusp, sino a lo largo de líneas de ligereza constante.
- El intervalo de ligereza usa la ligereza del color más oscuro en la gama en lugar del punto en el que el límite de la gama cruza el eje neutro.
- BasicPhoto admite un shell de gama de referencia y un shell de gama verosímil, si cualquiera de los límites de gama en la transformación tiene dos shells.
- BasicPhoto utiliza CIECAM02; en lugar de usar CIECAM97s para convertir a D65 a 400 cd/m2 y, a continuación, usar el espacio de colores RIT IPT.
El primer cambio se realizó para evitar problemas de inversión de tono que pueden producirse al usar la compresión hacia una cusp. Como se muestra en la figura 10, la compresión cusp puede provocar inversiones de tono. Esto puede ocurrir cuando los colores de alta cromática son más claros que los colores de cromática inferior. Dado que SGCK comprime cada píxel de forma independiente tanto en la ligereza como en el cromático, no se garantiza que conserve la relación de ligereza entre los valores de píxeles después de la compresión. La conocida desventaja de esta decisión de comprimir en líneas de ligereza constante es que puede sufrir pérdidas de cromática, en particular en áreas donde el límite de la gama de destino es muy plano, como sucede con amarillos brillantes.
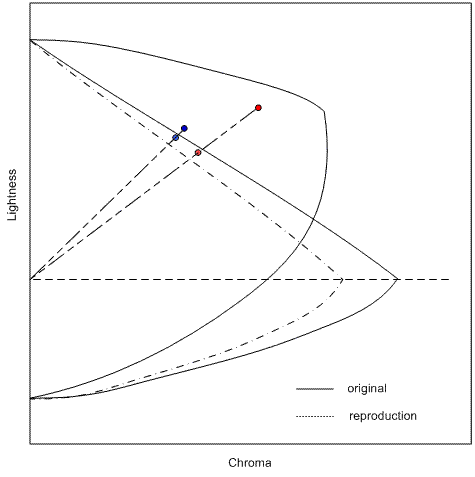
Figura 10 : Inversión de tono causada por SGCK



Figura 11: Imagen original, resultado SGCK y Resultado BasicPhoto
En la figura 11 se muestra esta inversión de tono. A la izquierda se muestra una imagen original capturada por una cámara digital; en el centro, la imagen como reproducida por SGCK; y a la derecha, la imagen como se reproduce en BasicPhoto. La imagen de la izquierda está en el espacio de colores de la cámara digital, las imágenes central y derecha se encuentran en el espacio de color de una pantalla de vídeo LCD. En la imagen original, la parte superior de la tetera es más oscura que la parte inferior, porque la parte inferior refleja el mantel sobre el que está sentado. En la imagen SGCK, la parte superior es realmente más ligera que la parte inferior, debido a la inversión de tono. Además, es difícil ver los elementos reflejados en la parte inferior de la tetera. A la derecha, BasicPhoto ha corregido la inversión de tono y los artículos reflejados son más claramente distintivos.
El segundo cambio se realizó para mejorar la reproducción de colores casi negros en impresoras donde el negro más negro no cae directamente en el eje neutro CIECAM02. En la figura 12 siguiente se muestra una imagen convertida en sRGB; reproducido para una impresora rgb de inyección de tinta utilizando SGCK; y se reproducen para la misma impresora con BasicPhoto. La imagen del centro no usa el dispositivo completo negro, por lo que carece del contraste visto en el original. El contraste se restaura con BasicPhoto.



Figura 12 : Negro mejorado
El tercer cambio se realizó para mejorar la reproducción de color para las cámaras digitales. Especialmente en los casos en los que la cámara digital se ha perfilado mediante un destino de referencia, una descripción de límite de gama creada a partir de colores medidos podría no incluir todos los colores que podrían capturarse en una escena real. En lugar de recortar todos los colores a la gama del destino de color medido, permite la extrapolación para producir un límite de gama verosímil. El algoritmo BasicPhoto está diseñado para admitir un límite de gama extrapolado.
El cuarto cambio se realizó porque CIECAM02 funciona bien para la asignación de la gama. El proceso recomendado por TC8-03 de convertir los colores del dispositivo a D65 a 400 cd/m2 y, a continuación, usar el espacio de color IPT de RIT es un proceso intensivo y lento.
Asignación de hue
HueMap es el equivalente de la intención de saturación icc.
Si el límite de la gama de origen o el límite de la gama de destino no contiene elementos principales, este modelo se revierte al modelo minCD (relativo) descrito en una sección anterior; por ejemplo, los dispositivos para los que no se pueden determinar los principales (perfiles ICC con más de cuatro canales) o perfiles ICC monocromáticos.
Este algoritmo ajusta primero el matiz del valor de color de entrada. A continuación, ajusta simultáneamente la ligereza y el cromático, utilizando una asignación de cizamiento. Por último, recorta el valor de color para asegurarse de que está dentro de la gama.
El primer paso es determinar el "Hue Wheels". Busque los valores de JCh para los colores principal y secundario para el dispositivo de origen y de destino. Solo está considerando los componentes de matiz. Esto da como resultado una rueda de matiz principal o secundaria con seis puntos de color para cada dispositivo. (Vea la figura 13).
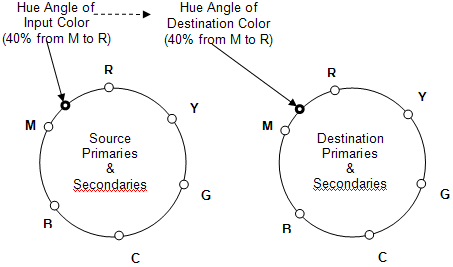
Figura 13 : Ruedas hue
Se pueden obtener mejores resultados si la principal azul de origen no se gira a la principal azul de destino. En su lugar, el ángulo de matiz principal azul de origen se usa como ángulo de matiz principal azul de destino.
A continuación, realice las rotaciones de matiz para cada color de entrada de la imagen de origen,
a)Con el ángulo de matiz del color de entrada, determine la ubicación del color en la rueda de matiz de origen en relación con los dos colores primarios o secundarios adyacentes. La ubicación se puede considerar como un porcentaje de la distancia entre las primarias. Por ejemplo, el matiz de color de entrada es el 40 por ciento del camino desde el valor de matiz de Magenta hasta el valor de matiz de Rojo.
b)En la rueda de matiz de destino, busque el ángulo de matiz asociado, por ejemplo, 40 por ciento de Magenta a Rojo. Este valor será el ángulo de matiz de destino.
En general, las primarias y secundarias de origen no estarán en los mismos ángulos de matiz que las primarias y secundarias de destino; es decir, el ángulo de matiz de destino normalmente será diferente del ángulo de matiz de origen.
Por ejemplo, supongamos que las ruedas de matiz producen los siguientes valores:
Origen M = 295 grados, Origen R = 355 grados.
Destino M = 290 grados, Destino R = 346 grados.
Si el ángulo de matiz del color de entrada es de 319 grados, es el 40 % del ángulo (24 grados) del origen M al origen R. El ángulo de M a R es de 60 grados y el ángulo de M al matiz de entrada es de 24 grados. Calcule el ángulo en el destino que es del 40 por ciento del destino M al destino R (22 grados), por lo que el ángulo de matiz del color de destino es de 312 grados.
A continuación, calcule los puntos de referencia de matiz para el matiz de origen y el matiz de destino. Para calcular el punto de referencia de matiz para un valor h (matiz) determinado, desea encontrar el valor J (ligereza) y el valor C (cromático).
- Busque el valor J del punto de referencia de matiz interpolando entre los valores J de los puntos primarios o secundarios adyacentes, utilizando la posición relativa del matiz; por ejemplo, 40 por ciento en este ejemplo.
- Busque el valor máximo de C en este valor J y h. Ahora tiene el JCh del punto de referencia de matiz para ese matiz.
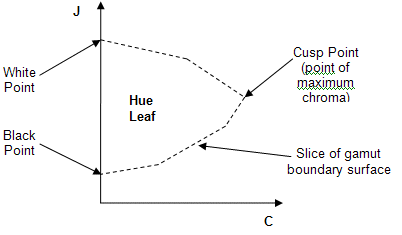
Figura 14 : Hoja de matiz (visualización de un segmento de límite de gama en un matiz específico)
El siguiente paso consiste en calcular la asignación de shear para cada píxel. En primer lugar, visualice una hoja de matiz desde la gama de origen para el ángulo de matiz de color de origen y una hoja de matiz desde la gama de destino para el ángulo de matiz de destino calculado durante la rotación de matiz. Las hojas de matiz se crean tomando un "segmento" de la superficie de límite de gama JCh en un ángulo de matiz específico (vea la figura 14).
NOTA: Por motivos de optimización del rendimiento, las hojas de matiz no se crean realmente; se describen y se muestran aquí solo con fines de visualización. Las operaciones se realizan directamente en la superficie de límite de la gama en el matiz especificado. A continuación, calcule los puntos de referencia de matiz para determinar la asignación de shear.
- Realice una escala de ligereza para asignar los puntos negros y blancos de la hoja de origen a la hoja de destino (vea la figura 15). Los puntos negros y blancos de la hoja de matiz de origen se asignan linealmente a los puntos negros y blancos de la hoja de matiz de destino, escalando todas las coordenadas J del límite de origen. El valor de color de entrada asignado a matiz se escala de la misma manera.
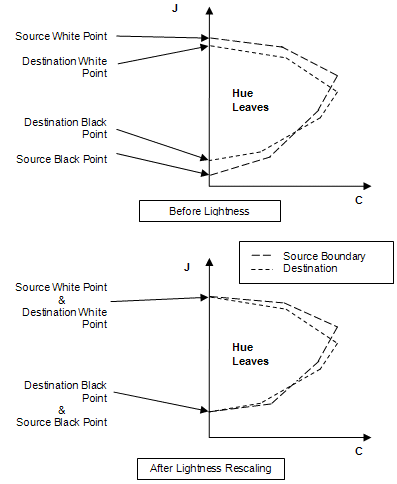
Figura 15: Asignación de ligereza
- Determine los puntos de referencia de matiz para cada hoja de matiz. Aplique una asignación de shear a la hoja de origen para que los puntos de referencia de origen y de destino coincidan (vea la figura 16). El punto de referencia de una gama en un matiz específico es el punto de referencia de matiz interpolado entre las principales adyacentes. El punto de referencia de la hoja de matiz de origen se asigna linealmente al punto de referencia de la hoja de matiz de destino, utilizando una operación de "shear" que bloquea el eje J, manteniendo los puntos negros y los puntos blancos estacionados. Los puntos negros, los puntos blancos y los puntos de referencia de las hojas de matiz de origen y destino deben coincidir.
- Aplique la asignación de shear al valor de color de entrada ajustado por la ligereza. Las coordenadas J y C del valor de color de origen se escalan proporcionalmente, en relación con su distancia desde el eje J.
- A continuación, se realiza una compresión sutil de la ligereza dependiente del cromática hacia el valor J del punto de referencia de tono en el punto de color asignado a la trama. La compresión hacia la referencia de matiz J se realiza de forma gamma, donde blanco, negro, grises y puntos en la referencia de tono J no se ven afectados. Todos los demás puntos tienden hacia la referencia de matiz J de manera suave, ligeramente agrupando cerca de la referencia de tono J, con constante restante de cromática. La dependencia cromática garantiza que los colores neutros no se ven afectados, y el efecto se incrementa en los colores con un mayor cromático.
A continuación se muestra una descripción matemática de la compresión de ligereza hacia la referencia de matiz J o ajustando el valor J del punto de destino. Se denomina punto de destino porque se ha asignado una estrabación en la gama de destino.
En primer lugar, calcule "factorC" (factor de dependencia cromática) para el punto de destino, lo que determina cuánto efecto tendrá la compresión de ligereza. Los puntos cercanos o en el eje J tendrán poca o ninguna compresión; los puntos más alejados del eje J (alta cromática) tendrán más compresión aplicada. Multiplique por 0,5 para asegurarse de que factorC es menor que 1, ya que es posible que sourceC pueda ser ligeramente mayor que referenceC, pero no dos veces igual de grande.
factorC = (destinationC/referenceC) ? 0.5
donde:
destinationC es el valor C del punto de destino.
referenceC es el valor C del punto de referencia de Hue.
A continuación, determine si el punto de destino J está por encima o por debajo de la referencia de tono J. Si es anterior, haga lo siguiente:
Calcule "factorJ" para el punto de destino en relación con el referenceJ. Este valor factorJ estará comprendido entre 0 y 1 (0 si está en el referenceJ; 1 si está en maxJ).
factorJ = (destinationJ - referenceJ) / (maxJ - referenceJ)
donde:
destinationJ es el valor J del punto de destino.
referenceJ es el valor J del punto de referencia de tono.
maxJ es el valor J máximo de la gama.
Aplique una función de potencia de tipo gamma a factorJ, lo que reducirá factorJ en una determinada cantidad. En este ejemplo se usa la potencia de 2 (el cuadrado). Reste el factorJ reducido del factorJ original y multiplique el resultado por el intervalo total de J por encima del referenceJ principal para encontrar el "deltaJ", que representa el cambio en J después de la compresión de ligereza, pero no incluye la dependencia cromática.
deltaJ = (factorJ - (factorJ ? factorJ)) ? (maxJ - referenceJ)
Aplique factorC al deltaJ (cuanto mayor sea el cromático, mayor será el efecto) y calcule el nuevo valor J para el punto de destino.
destinationJ = destinationJ - (deltaJ ? factorC)
Si el valor J para el punto de destino es inferior a referenceJ, se realiza un cálculo similar a los pasos anteriores A-C, usando minJ en lugar de maxJ para buscar el intervalo en J para calcular el factorJ y teniendo en cuenta la polaridad de las operaciones "debajo" del referenceJ.
factorJ = (referenceJ - destinationJ) / (referenceJ - minJ)
deltaJ = (factorJ - (factorJ ? factorJ)) ? (referenceJ - minJ)
destinationJ = destinationJ + (deltaJ ? factorC)
donde:
minJ es el valor J mínimo de la gama.
El cromático para los puntos de color de entrada se expande linealmente (cuando es posible) a lo largo de la ligereza constante proporcional al valor cromático máximo de las gamas de origen y destino en ese tono y ligereza. Combinado con la compresión de ligereza dependiente del cromático anterior, esto ayuda a preservar la saturación porque la asignación de escisiones mediante los puntos de referencia a veces hace que el punto de origen sobrecomprima en el cromático (véase la figura 16).
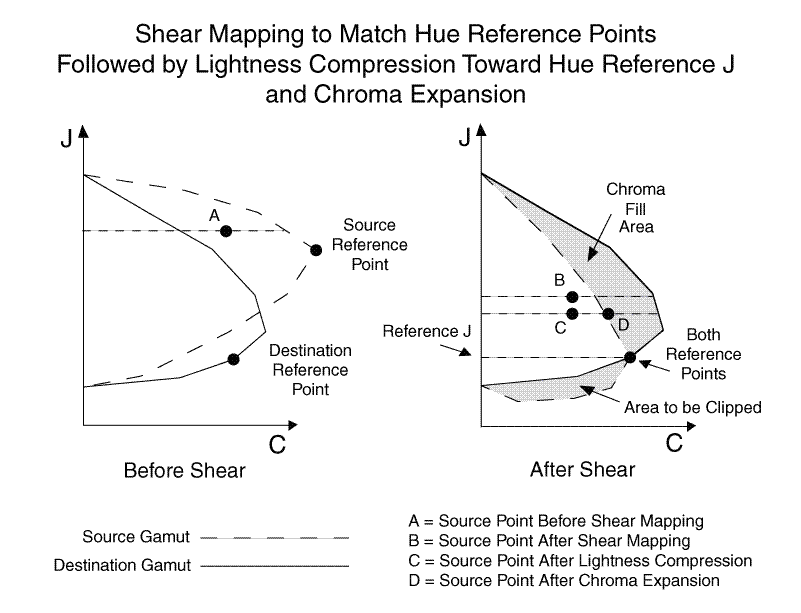
Figura 16 : Asignación de cizala, compresión de ligereza hacia la referencia de matiz J y expansión cromática
A continuación se muestra una descripción matemática del proceso de expansión cromática o ajustar el valor C del punto de destino. Se denomina punto de destino porque se ha asignado una asignación y una ligereza comprimidas en la gama de destino.
Antes de la asignación de cizalaje, determine sourceExtentC (la extensión cromática en la ligereza y el tono del punto de origen).
Después de la asignación y compresión de ligereza que transforma el punto de origen en el punto de destino, determine el destExtentC (la extensión cromática en la ligereza y el tono del punto de destino).
Si sourceExtentC es mayor que el destExtentC, no es necesario realizar ningún ajuste cromático en el punto de destino y puede omitir el paso siguiente.
Ajuste destinationC (el cromático del punto de destino) para ajustarse a la extensión cromática de destino en esta ligereza y matiz.
destinationC = destinationC ? (destExtentC/sourceExtentC)
donde:
destinationC es el valor C del punto de destino.
sourceExtentC es el valor C máximo de la gama de origen en la ligereza y el tono del punto de origen.
destExtentC es el valor C máximo de la gama de destino en la ligereza y matiz del punto de destino.
Por último, realice el recorte de distancia de mimimum. Si el color de entrada con tono girado, ajustado por la ligereza y el mapa de corte sigue ligeramente fuera de la gama de destino, guárdelo (muévalo) al punto más cercano del límite de la gama de destino (vea la figura 17).
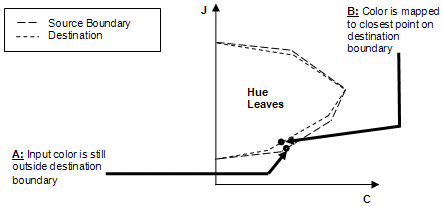
Figura 17 : Recorte de distancia mínima
Descripción del límite de gamut y algoritmos de shell de gama
La función de límite de gama de dispositivos usa el motor de modelo de dispositivo y los parámetros analíticos para derivar un límite de gama de dispositivos de color, descrito como una lista de vértices indizado del casco de la gama de dispositivos. El casco se calcula de forma diferente en función de si está trabajando con dispositivos aditivos, como monitores y proyectores, o dispositivos resta. La lista de vértices indizada se almacena en CIEJab. DirectX optimiza la estructura de la lista de vértices indexados para la aceleración de hardware.
Este enfoque tiene muchas soluciones conocidas. Si busca "Convex hull DirectX" en la Web, obtendrá más de 100 visitas. Por ejemplo, hay una referencia de 1983 en este tema específico (Teoría y aplicación de gráficos informáticos, "Shiphulls, superficies b-spline y cadcam", pp. 34-49) con referencias que datan de 1970 a 1982 en el tema.
La colección de puntos se puede determinar a partir de información disponible externamente, como se indica a continuación:
- Los puntos del shell de referencia para los monitores se generan mediante un muestreo del cubo de color en el espacio de color del dispositivo.
- Los puntos del shell de referencia para impresoras y dispositivos de captura se obtienen de los datos de ejemplo usados para inicializar el modelo.
- Los puntos del shell de referencia para scRGB y sRGB se generan mediante un muestreo del cubo de color para sRGB.
- Los puntos para el shell viable para los dispositivos de captura se generan mediante un muestreo del cubo de color en el espacio de color del dispositivo.
- Los puntos para el shell de referencia para proyectores se generan mediante un muestreo de un poliedro en el cubo de color en el espacio de color del dispositivo.
- Los puntos para el shell posible para los espacios de color de intervalo dinámico amplio se generan mediante un muestreo del cubo de color en el propio espacio.
Puede crear una lista de vértices que describa eficazmente la gama de dispositivos de color, dado un perfil de dispositivo y servicios de soporte técnico del sistema.
En el caso de los dispositivos de salida, el límite de la gama describe el intervalo de colores que el dispositivo puede mostrar. Se genera un límite de gama a partir de los mismos datos usados para modelar el comportamiento del dispositivo. Conceptualmente, se genera un muestreo del rango de colores que el dispositivo puede producir, medir los colores, convertir las medidas en espacio de apariencia y, a continuación, usar los resultados para crear el límite de gama.
Los dispositivos de entrada son más complicados. Cada píxel de una imagen de entrada debe tener algún valor. Cada píxel debe ser capaz de representar cualquier color que se encuentre en el mundo real de alguna manera. En este sentido, no hay colores "fuera de gama" para un dispositivo de entrada, ya que siempre se pueden representar.
Todos los formatos de imagen digital tienen un intervalo dinámico fijo. Debido a esta limitación, siempre hay algunos estímulos distintos que se asignan al mismo valor digital. Por lo tanto, no se puede establecer una asignación uno a uno entre los colores del mundo real y los valores de la cámara digital. En su lugar, el límite de gama se forma mediante la estimación de una gama de colores reales que pueden producir las respuestas digitales de la cámara. Use ese intervalo estimado como la gama para el dispositivo de entrada.
Las principales se incluyen para proporcionar la asignación de la gama de tipos de intención de gráficos empresariales.
En el estilo verdadero orientado a objetos, abstrae la representación subyacente del límite de la gama. Esto le permite cambiar la representación en el futuro. Para comprender el descriptor de límite de gama (GBD) usado en el nuevo CTE, primero debe comprender cómo funcionan los algoritmos de asignación de gama (GMG). Tradicionalmente, las AMG han sido diseñadas para satisfacer las necesidades de la comunidad de arte gráfico; es decir, para reproducir imágenes que ya se han representado correctamente para el dispositivo en el que se creó la imagen de entrada. El objetivo de las AMG de artes gráficas es hacer la mejor reproducción posible de la imagen de entrada en el dispositivo de salida. El nuevo GBD de CTE está diseñado para resolver cuatro problemas clave.
Dado que la imagen de entrada se representa para el dispositivo de entrada, todos los colores caben dentro del intervalo entre el punto blanco y el punto negro del medio. Supongamos que la imagen es una fotografía de una escena en la que hay un blanco difuso, como una persona en una camisa blanca y un resaltado especular, como la luz que refleja una ventana o un parachoques cromado. La escena se representará en el medio de entrada para que el resaltado especular se asigne al punto blanco del medio y el blanco difuso se asigna a un color neutro más oscuro que el punto blanco del medio. La elección de cómo asignar colores de la escena al medio de entrada es una decisión dependiente de la escena y una decisión estética. Si faltaba el resaltado especular de la escena original, el blanco difuso probablemente se asignaría al punto blanco del medio. En una escena con muchos detalles destacados, se dejaría más intervalo entre el blanco especular y el blanco difuso. En una escena en la que el resaltado no es significativo, es posible que quede un intervalo muy pequeño.
En el caso de las imágenes representadas previamente, la asignación de la gama es relativamente sencilla. Básicamente, el punto blanco del medio original se asigna al punto blanco del medio de reproducción, el punto negro de origen se asigna al punto negro de destino y la mayor parte de la asignación está completa. Las diferentes AMG en existencia proporcionan variaciones para asignar otros puntos en la escala de tono del medio de origen y diferentes formas de controlar los valores cromáticos fuera de gama. Pero la asignación de blanco a blanco y negro a negro es coherente a lo largo de estas variaciones. Esta implementación requiere que el blanco esté por encima de un J* de 50 y negro por debajo de un J* de 50.
No todas las codificaciones de color limitan los intervalos de colores para las imágenes de entrada. La codificación de color estándar IEC scRGB (IEC 61966-2-2) proporciona 16 bits para cada uno de los tres canales de color rojo, verde y azul (RGB). En esa codificación, el negro de referencia no está codificado como triple RGB (0, 0, 0, 0), pero como (4096, 4096, 4096, 4096). El blanco de referencia está codificado como (12288, 12288, 12288). La codificación scRGB se puede usar para representar resaltados especulares y detalles de sombra. Incluye triples RGB que no son físicamente posibles porque requieren cantidades negativas de luz y codificaciones que están fuera del locus espectral CIE. Claramente, ningún dispositivo puede producir todos los colores en la gama scRGB. De hecho, ningún dispositivo puede producir todos los colores que un ser humano puede ver. Por lo tanto, los dispositivos no pueden rellenar la gama scRGB y sería útil poder representar la parte de la gama que realizan. Cada dispositivo tiene un intervalo de valores en el espacio scRGB que puede producir. Estos son los colores "esperados" para el dispositivo; sería sorprendente que el dispositivo produzca colores fuera de esta gama. Hay una transformación definida del espacio scRGB al espacio de apariencia, por lo que cada dispositivo también tiene un intervalo de valores de apariencia que se espera que se reproduzca.
Tanto en scRGB como en la entrada de los dispositivos de captura caracterizados por un destino fijo, es posible obtener un valor fuera del intervalo de valores esperados. Si alguien calibra una cámara en un destino de prueba; y, a continuación, captura una escena con resaltados especulares, podría haber píxeles más brillantes que el punto blanco del destino. Lo mismo puede ocurrir si un rojo que se produce naturalmente es más cromático que el rojo objetivo. Si alguien toma una imagen scRGB de un dispositivo y, a continuación, edita manualmente los colores de la imagen, es posible crear píxeles que se encuentren fuera del intervalo esperado de la gama de dispositivos, aunque estén dentro de la gama completa scRGB.
Es posible que un segundo problema no, al principio, parezca estar relacionado con esto. Surge cuando se usa un destino de color para caracterizar un dispositivo de entrada, como una cámara o un escáner. Los objetivos reflectantes se suelen producir en papel y contienen una serie de parches coloreados. Los manufaturers proporcionan archivos de datos con medidas de color tomadas bajo una condición de visualización fija para cada revisión de color. Las herramientas de generación de perfiles de color crean una asignación entre estos valores medidos y los valores devueltos por los sensores de color en los dispositivos. El problema es que, a menudo, estos destinos de color no cubren toda la gama de valores de dispositivo. Por ejemplo, el escáner o cámara podría devolver un valor de (253, 253, 253, 253) para el punto blanco de referencia y una revisión roja de referencia podría tener un valor RGB de (254, 12, 4). Representan el intervalo de valores esperados para el dispositivo de entrada, en función de los valores de destino. Si caracteriza el dispositivo de entrada en función de las respuestas al destino, solo espera colores dentro de este intervalo estrecho. Este rango no solo es menor que el rango de colores que los seres humanos pueden ver, es más pequeño que el rango de colores que puede producir el dispositivo.
En ambos casos, es difícil calcular la gama del dispositivo de entrada o la imagen, a pesar de la existencia de una gama de referencias o medidas. En el primer problema, la gama verosímil del dispositivo de entrada es menor que la gama completa de scRGB. En el segundo problema, la gama de referencias del destino es menor que la gama completa posible del dispositivo de entrada.
El tercer problema implica la asignación de tono. Se han propuesto muchos modelos de límites de gama que pueden representar adecuadamente imágenes predepresentadas utilizadas en las artes gráficas, por ejemplo, el rango de montaña Braun y Fairchild GBD (Braun[97]) y el descriptor de límites Segment Maxima de Morovic (Morovic[98]). Pero estos modelos solo proporcionan información sobre los extremos de la gama del dispositivo; faltan información sobre otros puntos de la asignación tonal. Sin esta información, las AMG solo pueden realizar estimaciones aproximadas de la asignación de tono óptima. Peor, estos modelos no proporcionan ayuda para el rango dinámico extendido en scRGB y en imágenes de cámara digital.
¿Cómo se resuelve este problema en las industrias fotográficas y videográficas? La cámara captura una imagen. Los expertos podrían debatir la cantidad de representación que se produce en el dispositivo de captura; pero están de acuerdo en que no es una cantidad significativa. Ambas tecnologías no asignan un blanco difuso en una escena capturada al punto blanco del medio. Del mismo modo, no asignan el punto negro de la escena al punto negro del medio. El comportamiento de la película fotográfica se describe en el espacio de densidad utilizando una curva característica, a menudo denominada curva Hurter y Driffield, o H&D. La curva muestra la densidad de la escena original y la densidad resultante en la película. En la figura 18 se muestra una curva HD&típica. El eje x representa el aumento de la exposición del registro. El eje y representa la densidad de la diapositiva. Cinco puntos de referencia están marcados en la curva: negro sin detalle, que representa la densidad mínima en el negativo; negro con detalle; referencia tarjeta gris media; blanco con detalle; y blanco sin detalle. Tenga en cuenta que hay espacio entre negro sin detalle (que representa el dispositivo negro) y negro con detalle (negro de sombra). Del mismo modo, hay espacio entre blanco con detalle (blanco difuso) y blanco sin detalle (que representa el blanco del dispositivo).
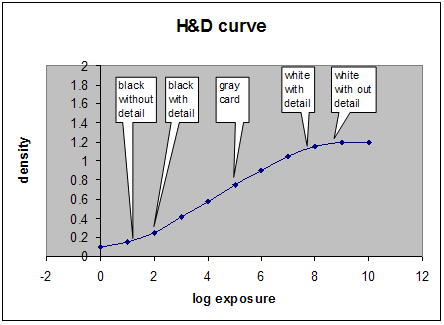
Figura 18 : Curva HD¶ la película con diapositivas
El sector del vídeo proporciona "headroom" y "footroom" en imágenes. En la especificación UIT 709, la luminancia (denominada Y) se codifica en 8 bits, con un intervalo de 0 a 255. Sin embargo, el negro de referencia se codifica en 15 y el blanco de referencia se codifica como 235. Esto deja el intervalo de codificación entre 236 y 255 para representar resaltados especulares.
El sector del vídeo presenta un sistema de bucles cerrados esencialmente. Aunque hay muchos proveedores de equipos diferentes, los sistemas de vídeo se basan en dispositivos de referencia. Hay una codificación estándar para imágenes de vídeo. No es necesario comunicar un límite de gama con imágenes de vídeo, ya que todas las imágenes se codifican para su reproducción en el mismo dispositivo de referencia. La película también está cerrada porque no es necesario transmitir datos intermedios entre distintos componentes. Quiere que una solución que permita reproducir imágenes de dispositivos con distintas gamas y que representen escenas pre renderadas y no representadas en la salida con diferentes gamas.
Un cuarto problema que debe resolver el nuevo CTE es que los colores visualmente grises producidos por un dispositivo, por ejemplo, cuando rojo=verde=azul en un monitor, con frecuencia no caen sobre el eje neutro de la CAM (cuando el cromático = 0,0). Esto provoca grandes dificultades para las AMG. Para que los GMG funcionen bien, debes ajustar la descripción de la gama del dispositivo y de los puntos de entrada para que el eje neutro del dispositivo se encuentre en el eje neutro del espacio de apariencia. Tiene que ajustar puntos fuera del eje neutro por una cantidad similar. De lo contrario, no se pueden realizar degradaciones suaves a través de la imagen. Al salir del GMA, deshace esta asignación en relación con el eje neutro del dispositivo de salida. Esto se conoce como un enderezamiento "desencadenado" del eje. Al igual que un chiropractor, no sólo endereza el esqueleto (eje neutro), sino que ajusta el resto del cuerpo para moverse junto con el esqueleto. Al igual que un chiropractor, no ajusta el esqueleto por la misma cantidad a través de todo el espacio. En su lugar, se ajustan diferentes secciones de forma diferente.
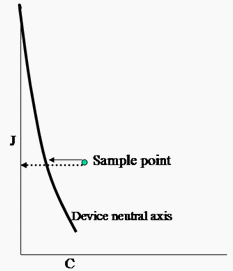
Figura 19: Curvatura del eje neutro del dispositivo en relación con el eje neutro CIECAM
Lo que requiere el nuevo CTE es un modelo de un límite de gama que se puede usar para representar imágenes de origen representadas y no representadas, proporcionar información sobre la apariencia de los neutros del dispositivo y proporcionar información para las imágenes de asignación de tono con una amplia gama de luminarias.
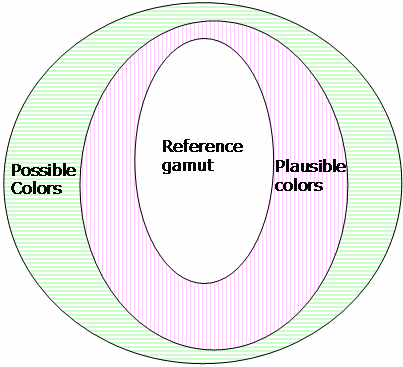
Figura 20 : Tres shells de gama
El límite de la gama se compone de tres shells que definen tres regiones.
En el nuevo CTE, el shell exterior de la gama se forma con un casco convexa hecho a partir de puntos de muestra en la gama de dispositivos. Un casco se forma tomando un conjunto de puntos de muestra y rodearlos por una superficie. Un casco convexo tiene la propiedad adicional de ser convexa en todas partes. Por lo tanto, este no es el casco más pequeño posible que puede ajustarse a los datos. Sin embargo, la experimentación ha demostrado que ajustar los puntos de muestra demasiado estrechamente provoca artefactos poco atractivos en imágenes, como una falta de sombreado suave. El casco convexo parece resolver estos problemas.
En el algoritmo, los valores de apariencia de color se obtienen para un conjunto de puntos muestreados desde el dispositivo. Para monitores e impresoras, los valores de apariencia de color se obtienen mediante la salida de muestras y, a continuación, medirlos. También puede crear un modelo de dispositivo y, a continuación, ejecutar datos sintéticos a través del modelo de dispositivo para predecir valores medidos. A continuación, los valores medidos se convierten del espacio colorimétrico (XYZ) al espacio de apariencia (Jab) y el casco se encapsula alrededor de los puntos.
El punto clave de este algoritmo es que el punto blanco adoptado usado en la conversión de colorimétrica al espacio de apariencia no tiene que ser el punto blanco del medio. En su lugar, puede seleccionar un punto más lejos dentro de la gama y en (o cerca) del eje neutro. Ese punto tendrá entonces un valor J de 100. Las muestras con un valor Y medido mayor que el punto blanco adoptado terminarán con un valor J mayor que 100.
Si coloca el punto blanco difuso de la escena como punto blanco adoptado para la conversión del espacio de color, los resaltados especulares de la escena se detectarán fácilmente como tener un valor J mayor que 100.
Dado que el modelo de color CIECAM02 se basa en el sistema visual humano, después de seleccionar un blanco adoptado, el nivel de luminancia del punto negro (J = 0) se determina automáticamente por el modelo. Si la imagen de entrada tiene un amplio intervalo dinámico, es posible que haya valores que se asignen a valores J inferiores a cero.
En la figura 21 siguiente se muestran los neutrales del dispositivo que se ejecutan a través del centro de las gamas de referencia y verosímiles.
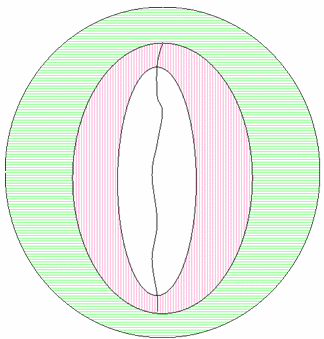
Figura 21 : Eje neutro del dispositivo agregado al límite de gama
Todas las asignaciones de gama implican recortar un intervalo de entrada a una gama de salida o comprimir la gama de entrada para ajustarse a la gama de salida. Los algoritmos más complejos se forman comprimiendo y recortando en diferentes direcciones, o dividiendo la gama en regiones diferentes y realizando recortes o compresión en las diferentes regiones.
El nuevo CTE amplía este concepto para admitir las regiones de una posible gama, una gama verosímil y una gama de referencias, y permite a las AMG asignarlas de diferentes maneras. Además, los GMA tienen información sobre el eje neutro del dispositivo. En la siguiente discusión se explica cómo controlar situaciones en las que las series y las series de referencia verosímiles se han contraído entre sí.
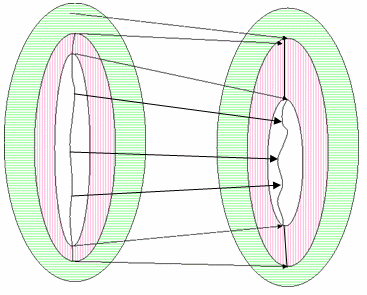
Figura 22 : GMA con dos descriptores de gama no contraídos
Es posible que vea este ejemplo si asigna desde un dispositivo de entrada, como una cámara o un escáner que se caracteriza por un destino reflectante, a un espacio scRGB. Aquí los colores factibles que son más claros que el blanco de referencia son resaltados especulares. En la práctica, la caracterización de una cámara con un destino podría no generar el rango completo de valores posibles en la cámara; sin embargo, los resaltados especulares y los colores cromáticos encontrados en la naturaleza serían. (Los destinos transmisivos suelen tener una revisión que es la densidad mínima posible en el medio. Con este objetivo, los resaltados especulares caerían dentro del intervalo del objetivo). El negro de referencia para un destino reflectante sería el principio de la región negra de sombra. Es decir, es probable que haya colores en las sombras que sean más oscuros que el negro en el objetivo. Si la imagen contiene un montón de contenido interesante en esa región, puede que valga la pena conservar esa variación tonal.
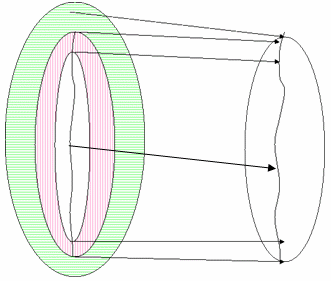
Figura 23 : GMA con la gama de destino contraída
En la figura 23 se muestra un posible algoritmo de asignación de gama cuando la gama de destino solo proporciona el intervalo de blanco a negro del dispositivo y no hay colores posibles fuera de esta gama. Esto es probable que suceda en dispositivos de salida típicos, como impresoras. Los colores posibles se asignan al borde de la gama de destino. Pero carece de una curva de tono para el dispositivo de salida. El GMA debe seleccionar algún punto neutro de la luminancia inferior para usarlo como destino de asignación para el blanco de referencia. Un algoritmo sofisticado puede hacerlo mediante histogramas que hacen histogramas en la imagen de origen y viendo cuántas caídas están en el intervalo de lo esperado pero más claro que el blanco de referencia. Cuantos más ligeros, más espacio se requiere en el dispositivo de destino entre los puntos asignados para los resaltados especulares y el blanco de referencia. Un algoritmo más sencillo podría seleccionar una distancia arbitraria hacia abajo la escala de ligereza del blanco del dispositivo, como el 5 por ciento. Se aplica un enfoque similar para la asignación del negro máximo y negro de sombra.
Después de generar la curva de tono de destino, puede asignar en un método similar al usado en la figura 23 anterior. Todos los puntos de la curva de tono de destino estarán dentro de la gama del dispositivo y todos los puntos de la asignación deben estar dentro de la gama de dispositivos.
Si invierte las figuras izquierda y las figuras derechas, y las direcciones de las flechas de la figura 23, puede describir el caso en el que la imagen de origen solo tiene una gama de referencias y las tres gamas del dispositivo de salida no se han contraído entre sí. Un ejemplo de esto podría ser la asignación de un monitor a scRGB. De nuevo, el GMA debe sintetizar los puntos de control de los cinco puntos de la curva de tono de la imagen de origen. Algunas asignaciones podrían colocar todos los puntos de la curva de tono dentro de la gama de dispositivos scRGB, mientras que otras asignaciones podrían usar más de la gama scRGB asignando blanco difuso al blanco de referencia y permitiendo que el blanco especular se asigne a un valor más claro.
Por último, tiene el caso en el que ambos dispositivos solo tienen la gama de referencia, que es cómo funcionan la mayoría de los algoritmos de asignación de gama. Por lo tanto, puede resolverlo simplemente retrocediendo a los algoritmos actuales. Como alternativa, si tiene una manera razonable de determinar los cinco puntos de referencia para los dispositivos de origen y destino, puede organizar el mapa de los puntos de referencia.
Las gamas de dispositivos contienen más de los cinco puntos de referencia en el eje neutro. Estos solo representan los límites entre las posibles regiones de la imagen. Entre cada uno de los puntos de referencia, puede usar cualquiera de las técnicas de asignación de gama existentes. Por lo tanto, puede recortar el rango de colores inesperados y comprimir todos los colores entre el blanco y el negro esperados, o puede recortar todos los colores fuera del rango de referencia y comprimir dentro de ese rango. Hay muchas posibilidades, que se pueden implementar en diferentes AMG. Además, las AMG pueden comprimir y recortar de diferentes maneras. Todas esas combinaciones se tratan dentro de esta invención.
Hasta ahora en esta discusión, la gama se ha tratado como si fuera únicamente una función del dispositivo en el que se creó, capturó o mostró la imagen. Sin embargo, no hay ninguna razón por la que todas las imágenes de un dispositivo deben tener la misma gama. Las AMG dependen de los datos de GBD. Si el descriptor se cambia entre imágenes, no hay forma de que los OMG sepan. En concreto, si las imágenes no tienen resaltados especulares, los GMG funcionan mejor si el descriptor de gama no muestra que hay colores más claros que el blanco difuso.
En la nueva arquitectura de CTE, es posible usar más de una GMA. El uso de varias AMG es intrínsecamente mal definido. Por ejemplo, si un dispositivo de captura asocia una GMA con su "apariencia y apariencia", tiende a hacerlo con una gama de destino "dirigida". Lo mismo sucede con los dispositivos de salida y las gamas de origen "dirigidas". La gama sRGB es una gama implícita dirigida normalmente. Por lo tanto, se recomienda encarecidamente usar una sola GMA, si la previsibilidad es una prioridad. Un único flujo de trabajo de GMA debe ser el valor predeterminado para todos los flujos de trabajo, especialmente los flujos de trabajo de consumidor y prosumer. Aunque la asignación de la gama para la reproducción preferida debe realizarse una vez, hay instancias en las que se incluyen varios procesos de asignación. En primer lugar, para la corrección, realiza una asignación preferida a la gama del dispositivo de destino final y, a continuación, una representación de colorimétrica en la gama del dispositivo de corrección. En segundo lugar, algunos tipos de asignación se usan para modificar las características de la imagen, pero no se incluyen para asignar a una gama de dispositivos, por ejemplo, ajustar la curva de tono o la cromática. Si se usan varias AMG, la interfaz de transformación toma una matriz de asignaciones de gama enlazadas, es decir, mapas de gama que se han inicializado con un par de descripciones de límites de gama. Cuando hay más de un mapa de gama, el límite de la gama de entrada para un mapa de conmutación de gamut correcto debe ser el mismo que el límite de la gama de salida de su predecesor.
La función de límite de gama de dispositivos toma el motor de modelo de dispositivo y los parámetros analíticos y deriva un límite de gama de dispositivos de color descrito como una lista ordenada de vértices del casco convexa de la gama de dispositivos. La lista ordenada de vértices se almacena en CIEJab. La estructura de la lista de vértices ordenada está optimizada para la aceleración de hardware mediante DirectX. Este enfoque tiene muchas soluciones conocidas (busque "convex hull DirectX" en la web y obtenga más de 100 visitas). También hay una referencia de 1983 en este tema (Teoría y aplicación de gráficos informáticos, "Shiphulls, superficies b-spline y cadcam" pp. 34-49), con referencias que datan de 1970 a 1982 sobre el tema.
Se pueden usar dos técnicas diferentes para calcular los triángulos en el shell de gama. Para otros dispositivos distintos de los dispositivos RGB aditivos, se calcula un casco convexa. Puede considerar la posibilidad de investigar la compatibilidad con casco no convexa para otros dispositivos si tiene acceso directo a estos dispositivos para validar la solidez, el rendimiento y la fidelidad de los algoritmos. Se trata de un proceso conocido que no requiere una descripción adicional. La técnica utilizada para dispositivos RGB aditivos se describe de la siguiente manera.
Los diferentes GBD tienen ventajas y desventajas. La representación del casco convexa garantiza propiedades geométricas agradables, como segmentos de tono convex que proporcionan un punto de intersección único con un rayo que emana de un punto en el eje neutro. La desventaja de la representación del casco convexa también es convexidad. Se sabe que muchos dispositivos, específicamente dispositivos de visualización, tienen gamas que están lejos de ser convexas. Si la gama real se desvía significativamente de la suposición de convexidad, la representación del casco convexa sería inexacta, posiblemente en la medida en que no representa la realidad.
Después de adoptar un GBD que proporciona una representación razonablemente precisa de la gama real, surgen otros problemas, algunos debido al concepto mismo de segmento de tono. Hay al menos dos situaciones patológicas. En la figura 24 siguiente, una gama CRT da lugar a segmentos de tono con "islas". En la figura 25, una gama de impresoras da lugar a un segmento de tono con parte del eje neutro ausente. Los segmentos patológicos de matiz no son causados por límites de gama patológica particularmente patológicos en estos casos. Son causadas por el concepto de segmento de tono, porque (a) se toma a lo largo del tono constante, y (b) solo toma una mitad del plano que corresponde al ángulo de tono.
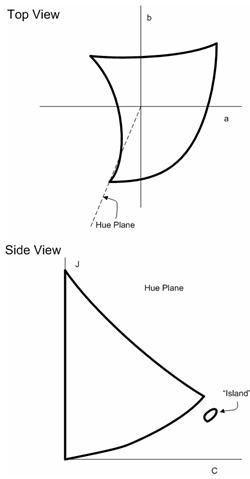
Figura 24 : Un monitor CRT típico tiene una gama que muestra peculiares "curving in" en los tonos azules. Si se toman segmentos de tono dentro de este intervalo de matiz, las islas aisladas pueden aparecer en los segmentos de tono.
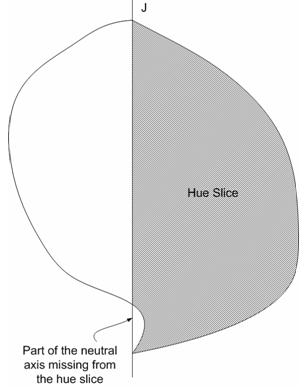
Figura 25 : Una impresora puede tener una gama que tenga una "brecha" en su eje neutro. Cuando se toma un segmento de tono (que es solo una mitad del plano), hay una "dent" en la parte del límite que es el eje neutro. Esto puede ser difícil de resolver de forma algorítmica.
Para resolver estas patologías, se propone un nuevo marco que abandona el concepto de segmento de matiz que se usa como punto de partida. En su lugar, el marco usa el conjunto de "elementos de línea de límite" o líneas que se encuentran en el límite de gama. No proporcionan necesariamente una visualización geométrica coherente como segmentos de tono, pero admiten todas las operaciones comunes de gama. Además de resolver los problemas mencionados anteriormente, este enfoque también sugiere que la construcción de segmentos de matiz, incluso cuando es posible, es computacionalmente desperdiciado.
Triangulación del límite de gama
El punto de partida es un GBD que consta de una triangulación del límite de la gama. Los métodos conocidos de construcción de GBD suelen proporcionar esa triangulación. Para la concretación, aquí se describe un método de construcción de GBD para dispositivos aditivos que su espacio de dispositivos se describe aquí. Estos dispositivos incluyen monitores (basados en CRT y basados en LCD) y proyectores. La geometría simple del cubo permite introducir una red regular en el cubo. Las caras de límite del cubo se pueden triangular de una serie de modas, como la que se muestra en la figura 26. La arquitectura proporciona un modelo de dispositivo para el dispositivo para que los valores colorimétricos de los puntos de lattice se puedan obtener de forma algorítmica o se hayan realizado medidas directamente para esos puntos. La arquitectura también proporciona CIECAM02, para que pueda suponer que los datos iniciales ya se han asignado al espacio de jab CIECAM02. A continuación, cada punto de celosía en las caras de límite del cubo RGB tiene un punto correspondiente en el espacio Jab. Las conexiones de puntos que forman el conjunto de triángulos en el espacio RGB también inducen un conjunto de triángulos en el espacio Jab. Este conjunto de triángulos forma una triangulación razonable del límite de la gama si (a) la red en el cubo RGB es lo suficientemente fina, y (b) la transformación del espacio del dispositivo al espacio de color uniforme se comporta de forma topológica; es decir, asigna el límite al límite y no gira la gama dentro de fuera para que los puntos interiores se conviertan en puntos de límite.
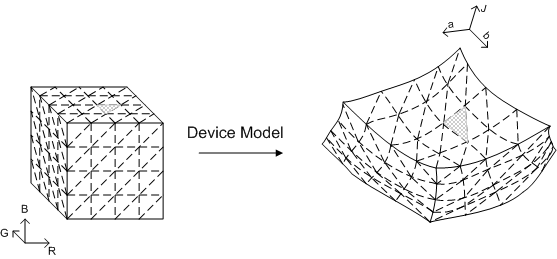
Figura 26 : Método simple para triangular el límite de la gama de un dispositivo con RGB como espacio de dispositivo
Elementos de línea de límite
Central para este marco es el concepto de elementos de línea de límite; un conjunto de segmentos de línea que (a) se encuentran en el límite de la gama y (b) se encuentran en un plano. En este caso, el plano es un plano de matiz. Cada segmento de línea es el resultado de intersecr el plano con un triángulo de límite de gama. Aunque muchos investigadores han usado la construcción de intersección de un plano con triángulos de límite, generalmente analizan la relación entre estos segmentos de línea e intentan construir un objeto geométrico coherente fuera de los segmentos de línea. Se han diseñado diferentes algoritmos para seguir estos segmentos de línea uno después del otro hasta que se obtiene un segmento de matiz completo y se han intentado acelerar el proceso de búsqueda.
Este enfoque es diferente. Intersecte el plano con los triángulos para obtener los segmentos de línea. A continuación, considere estos segmentos de línea como los objetos conceptuales básicos . Es necesario analizar la relación entre los segmentos de línea; no tienes que saber cómo están interconectados entre sí. Este punto de vista resuelve el problema de la segmentación de matiz con islas. Los enfoques conocidos que intentan construir segmentos de matiz suponen que, si uno comienza con un segmento de línea y lo sigue al siguiente segmento de línea, etc. finalmente conduce al punto inicial, en el que se construiría un segmento de matiz completo. Desafortunadamente, este enfoque perdería la isla (y en el peor escenario, el continente). Al no insistir en obtener una imagen geométrica coherente; es decir, segmento de matiz, puede manejar el problema de la isla sin esfuerzo. Otra diferencia importante en este enfoque es que, para acelerar la construcción de segmentos de línea, usa un "filtro de triángulos". El filtro de triángulo produce ciertos triángulos que definitivamente no generarán segmentos de línea que serían útiles en la operación de gama actual. Dado que la intersección de un triángulo con el plano es costosamente computacional, esto mejora la velocidad. Un efecto secundario es que, no se puede construir un segmento de matiz porque faltarían algunos segmentos de línea debido al filtrado de triángulos.
Operación de gamut: CheckGamut
En el ejemplo siguiente se explica cómo funciona el marco y cómo se lleva a cabo CheckGamut, es decir, el funcionamiento de comprobar si un color está en gamut.
El marco general se muestra en la figura 27 siguiente. Hay varios componentes. Los componentes etiquetados en cursiva son componentes que pueden ser diferentes en la implementación en función de la operación de gama en cuestión. Los demás componentes son invariables en todas las operaciones de gama. Para comenzar, input es un conjunto de atributos de color. En el caso de CheckGamut, es el color de la consulta. En la figura 27 y la siguiente explicación, se supone que el ángulo de matiz está entre los atributos de color de entrada o se puede obtener de ellos. Este es claramente el caso si la entrada es el punto de color completo, ya sea en Jab o JCh, desde el que puede calcular el ángulo de matiz. Tenga en cuenta que el ángulo de matiz solo es necesario porque se usan planos de matiz. En función de la operación de gama en cuestión, es posible que no sea necesario usar el plano de matiz. Por ejemplo, en la construcción de la rutina CheckGamut, es posible que desee usar planos de constante J. Se trata de una generalidad que no se usará ni analizará más a fondo; pero puede resultar útil recordar esta flexibilidad de la metodología para admitir otras operaciones de gama cuando el plano de matiz podría no ser la mejor opción.
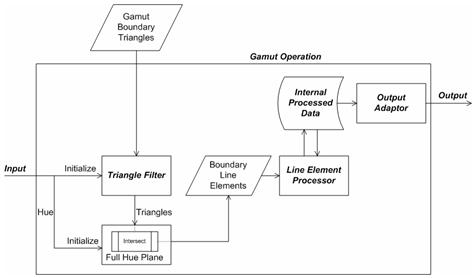
Figura 27 : Marco para admitir operaciones de gama
El ángulo de matiz, que se obtiene directamente de las entradas o se calcula a partir de las entradas, se usa para inicializar el plano de matiz con la etiqueta Full Hue Plane en la figura. "Lleno" se destaca porque es el plano completo, no solo el plano medio que contiene el matiz. El plano completo contiene el ángulo de matiz de entrada y el ángulo 180 grados opuestos a él. La funcionalidad clave del plano de matiz es la función Intersect, que se explica en la siguiente subsección, Plano de hue completo: Intersect. Supongamos que el GBD ya se ha construido y que el conjunto de triángulos de límite de gamut está disponible. Intersecte los triángulos que han sobrevivido al filtro de triángulos con el plano de matiz mediante Intersect. El componente Filtro de triángulos se etiqueta en cursiva, lo que significa que el componente varía en la implementación de diferentes operaciones de gama. El filtro triángulo para CheckGamut se explica en la sección Operación de gamut: CheckGamut (continuación). El resultado de intersecr un triángulo con el plano de matiz está vacío o un elemento de línea de límite , es decir, un par de puntos distintos. Si el resultado no está vacío, se pasa al procesador de elementos de línea , que de nuevo realiza diferentes cosas en función de la operación de gama. El procesador de elementos de línea actualiza la estructura de datos interna, Datos procesados internos , cuyo contenido o diseño también depende de la operación de gama. Por lo general, los datos procesados internos contienen la "respuesta" al problema, que se actualiza continuamente con cada nuevo elemento de línea de límite encontrado. Cuando se han procesado todos los elementos de línea de límite, se ha encontrado la respuesta. Permanece para acceder a él a través del adaptador de salida. Dado que los datos procesados internos son específicos de la operación de conversión, el adaptador de salida también es específico de la operación de conversión.
Plano de Hue completo: Intersección
La función Intersect calcula la intersección del plano de matiz y un triángulo. Tan simple como suena, esta función es importante por dos motivos.
En primer lugar, la intersección de cada borde del triángulo con el plano podría producir tres puntos de intersección, una situación geométricamente imposible. La razón por la que esto puede ocurrir en el cálculo es que, cuando los cálculos se realizan en punto flotante, por ejemplo, el formato IEEE, hay incertidumbres o "ruido numérico", en cada paso que afecta a la conclusión de si un borde cruza el plano. Cuando el plano interseca los bordes en una situación casi extraña, los puntos de intersección están cerca entre sí y la determinación de si un punto de intersección se encuentra dentro del borde es aleatorio. Aunque el ruido en los valores numéricos de los puntos es pequeño, la conclusión cualitativa de que hay más de dos puntos de intersección es geométricamente imposible y difícil de controlar correctamente en el algoritmo.
En segundo lugar, esta función está en el bucle crítico para cada borde de cada triángulo filtrado, por lo que es importante optimizar su eficiencia tanto como sea posible.
Para solucionar el primer problema de ruido numérico, realice los cálculos en enteros. Para solucionar el segundo problema de optimización de su eficacia, almacene en caché el atributo más usado de cada vértice o el "producto de puntos" asociado a cada vértice. Pasar enteros es una manera típica de garantizar la coherencia geométrica. La idea básica es que si tienes que cuantizar, hazlo al principio. A continuación, los cálculos posteriores se pueden realizar en enteros y, si los enteros son lo suficientemente anchos como para que no haya peligro de desbordamiento, los cálculos se pueden realizar con precisión infinita. La siguiente función de cuantificación resulta útil para este propósito.
ScaleAndTruncate(x) = Parte entera de x*10000
El factor de escalado 10000 significa que el número de punto flotante de entrada tiene cuatro posiciones decimales, lo que es lo suficientemente preciso para esta aplicación. Según el intervalo de valores del espacio de apariencia de color, desea elegir un tipo entero con bits lo suficientemente anchos como para contener los cálculos intermedios. En la mayoría de los espacios de apariencia de color, el intervalo de cada coordenada está dentro del intervalo de -1000 a 1000. La coordenada cuantificada tiene un valor absoluto máximo posible de 10 000*10 000 = 10 000 000. Como verá, la cantidad intermedia es un producto de puntos, que es una suma de dos productos de coordenadas, por lo que tiene un valor absoluto máximo posible de 2*(10.000.000) ₁₄. El número de bits necesarios es el registro (2?10 ₁₄ ) = 47,51. Una opción cómoda para el tipo entero es, por lo tanto, enteros de 64 bits.
Para garantizar que la intersección de un plano con un triángulo siempre proporciona un conjunto vacío o un conjunto de dos puntos, debe considerar el triángulo en su conjunto, no como bordes individuales del triángulo por separado. Para comprender la situación geométrica, considere las "distancias firmadas" de los vértices del triángulo desde el plano de matiz. No calcule estas distancias firmadas directamente; en su lugar, calcule los productos de puntos de los vectores de posición de los vértices con el vector normal cuantificado al plano. Más concretamente, durante la inicialización del plano de matiz, el vector normal cuantificado se calcula de la siguiente manera.
NormalVector = (ScaleAndTruncate(-sin(hue)), ScaleAndTruncate(cos(hue)))
Tenga en cuenta que este vector es un vector bidimensional. Puede usar un vector bidimensional porque el plano de matiz es vertical, por lo que el tercer componente del vector normal siempre es cero. Además, se inicializa una tabla de búsqueda de productos de puntos para tener una entrada para cada vértice de los triángulos de límite de gamut y el producto de punto correspondiente establecido en un valor no válido.
Durante una operación de intersección del plano de matiz con un triángulo, se busca el producto de punto de cada vértice del triángulo. Si el valor de la tabla de búsqueda es el valor no válido, el producto de puntos se calcula mediante la expresión siguiente.
NormalVector.a*ScaleAndTruncate(vertex.a) + NormalVector.b*ScaleAndTruncate(vertex.b)
De nuevo, el componente J del vértice nunca se usa, porque el vector normal es horizontal. Después, este producto de punto se guarda en la tabla de búsqueda para que no tenga que volver a calcularse si el producto de puntos del vértice se consulta más adelante.
El almacenamiento en caché permite determinar rápidamente si un borde cruza el plano, una vez que los productos de puntos se tabulan en la tabla de búsqueda, que se crea progresivamente a medida que se procesan los vértices.
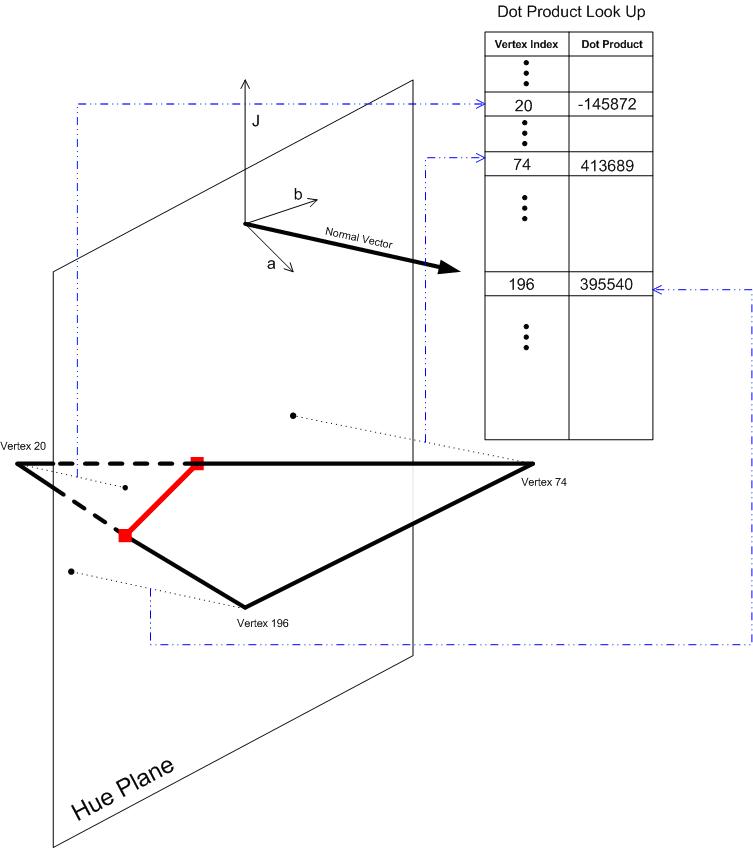
Figura 28 : Intersección del plano de matiz con un triángulo
Para que el triángulo de la figura 28 intersece el plano de matiz en un segmento de línea no degenerado, los productos de puntos de los vértices deben estar en uno de los patrones siguientes, cuando se ordenan en orden ascendente.
0,0,+; -,0,0; -,0,+; -,-,+; -,+,+
Un punto final del segmento de línea surge cuando el plano se interseca mediante un borde con vértices que tienen signos diferentes en el producto de puntos. Si el signo es cero, el vértice se encuentra justo en el plano y la intersección del borde con el plano es el propio vértice. Tenga en cuenta también que los casos son 0,0,0; -,-,0; 0,+,+ no se notifican. El primer caso (0,0,0) significa que todo el triángulo se encuentra en el plano. Esto no se notifica porque cada borde del triángulo debe pertenecer a un triángulo vecino que tampoco se encuentra completamente en el plano. El borde se notificará cuando se considere ese triángulo. Los otros dos casos (-,-,0 y 0,+,+) corresponden a la configuración geométrica que el triángulo toca el plano en un vértice. Estos casos no se notifican porque no dan lugar a un segmento de línea no degenerado.
El algoritmo anterior determina cuándo calcular una intersección entre un borde del triángulo y el plano de matiz. Una vez determinado un borde, la intersección se calcula mediante ecuaciones paramétricas. Si uno de los productos de puntos es cero, la intersección es el propio vértice, por lo que no es necesario realizar ningún cálculo. Suponiendo que ambos productos de puntos de los vértices del borde son distintos de cero, el vértice1 es el vértice con punto negativo product dotProduct1; y vértice2 es el vértice con un punto positivo dotProduct2. Este orden es importante para asegurarse de que el punto de intersección calculado no depende de cómo aparezca el orden de los vértices en la representación del borde. El concepto geométrico del borde es simétrico con respecto a sus vértices. El aspecto computacional del uso de ecuaciones paramétricas del borde presenta asimetría (elección del vértice inicial), que puede dar un punto de intersección ligeramente diferente debido al ruido numérico y el acondicionamiento de las ecuaciones lineales que se van a resolver. Dicho esto, el punto de intersección, intersección, se da a continuación.
t = dotProduct1/(dotProduct1 - dotProduct2)
Intersección. J = vértice1. J + t * (vértice2. J - vértice1. J)
intersection.a = vertex1.a + t * (vertex2.a - vertex1.a)
intersection.b = vertex1.b + t * (vertex2.b - vertex1.b)
Operación de gamut: CheckGamut (continuación)
El algoritmo geométrico básico que se usa para la comprobación de la gama es contar el número de cruces de rayos. Para un punto de consulta determinado, considere un rayo que comienza con el punto de consulta y apunta hacia arriba (dirección J). Contar el número de veces que este rayo cruza el límite de la gama. Si este número es par, el punto de consulta está fuera de rango. Si este número es impar, el punto está dentro. En principio, este algoritmo se puede implementar en 3D, generalmente se ve afectado por dificultades causadas por situaciones degeneradas, como el rayo que se encuentra (en parte) en un triángulo de límite o la degeneración dimensional inferior, como el rayo que se encuentra (en parte) en un borde de un triángulo de límite. Incluso en 2D, tienes que lidiar con estas situaciones degeneradas; pero el problema es más sencillo y se ha abordado de manera satisfactoria. Véase [O'Rourke].
Para un punto de entrada determinado Jab, determine su ángulo de matiz h como se indica a continuación.
h = atan(b/a),
Inicialice el plano de matiz y, a continuación, determine los elementos de línea de límite correspondientes a este plano de matiz. Dado que los elementos de línea de límites solo son relevantes si cruzan el rayo hacia arriba, configure un filtro de triángulos para quitar triángulos que proporcionan elementos de línea que definitivamente no intersecarán el rayo ascendente. En este caso, considere el rectángulo delimitador del triángulo. El rayo ascendente no intersecará el triángulo si el punto de consulta está fuera de la "sombra" que convierte el cuadro de límite si una fuente de luz estaba directamente encima. Infla esto ligeramente con una tolerancia pre-fija para permitir ruido numérico para que no descarte accidentalmente triángulos que puedan proporcionar elementos de línea útiles. El resultado es el cilindro rectangular semiin infinito que se muestra en la figura 29. Comprobar si el punto de consulta está dentro o fuera de este cilindro se puede implementar eficazmente mediante desigualdades simples.
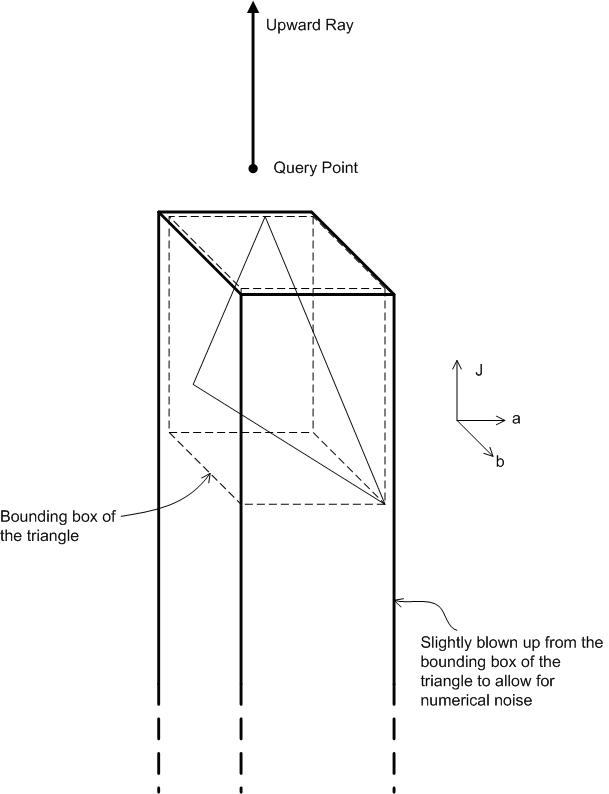
Figura 29 : Filtro de triángulo para CheckGamut
CheckGamut tiene tres componentes específicos de la operación de gama: datos procesados internos, procesador de elementos de línea y adaptador de salida. Los datos procesados internos son una lista de elementos de línea procesados por el procesador de elementos de línea. En este caso, el procesador de elementos de línea simplemente agrega un elemento de línea a la lista. La estructura de datos interna para datos procesados internos puede ser una lista vinculada o una matriz que puede crecer en tamaño.
El adaptador de salida es un módulo que accede a la lista de elementos de línea, determina si un elemento de línea cruza el rayo ascendente (recuento 1) o no (recuento 0). La suma de todos estos recuentos proporciona un recuento total. El adaptador de salida genera en última instancia una respuesta de "sí" (en gamut) o "no" (fuera de la gama), dependiendo de si el recuento total es impar o incluso. El paso en el que se determina si un elemento de línea cruza el rayo ascendente merece cierta atención, ya que aquí es donde surge el problema de degeneración y también surge el problema del exceso de recuento. Después de [O'Rourke], para que un elemento de línea cruce el rayo, el extremo derecho (el punto final con cromática más grande) debe estar estrictamente en el lado derecho del rayo. Esto garantiza que, si un punto final alguna vez se encuentra exactamente en el rayo, solo se cuenta una vez. La misma regla también resuelve la situación degenerada en la que el elemento de línea se encuentra exactamente en el rayo. No se incrementa el recuento de este elemento de línea.
En la figura 30 se muestran los elementos de línea resultantes de una gama de muestras con el punto de consulta en varias posiciones.
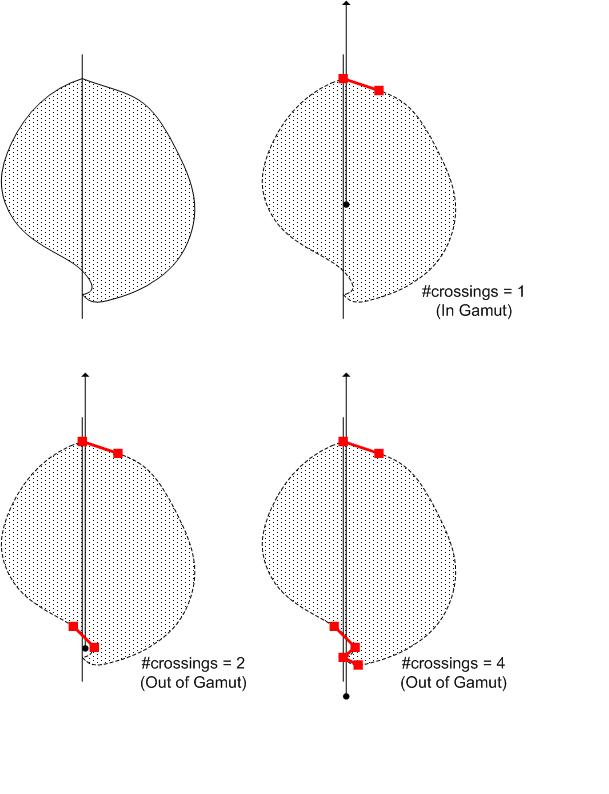
Figura 30 : Funcionamiento de CheckGamut
Asignación de gama mínima de diferencia de color
La asignación de gama mínima de diferencia de color, MinDEMap, tiene una especificación simple: si un color está en gamut, no haga nada. Si un color está fuera de gama, muestralo al punto "más cercano" en el límite de la gama. La palabra clave "más cercana" no está bien definida hasta que se especifica la ecuación de diferencia de color que se va a usar. En la práctica, para facilitar y acelerar el cálculo, la distancia euclidiana del espacio de apariencia de color elegido, o una variante de ella, se usa como métrica de diferencia de color. La ventaja de la métrica euclidiana es que es compatible con el producto de puntos del espacio, lo que permite usar el álgebra lineal. En detalle, si se define un "producto de puntos" en el espacio, se puede definir una distancia como la raíz cuadrada del producto de punto del vector de diferencia con sí mismo. Un producto de punto generalmente se puede definir mediante una matriz positiva 3x3 A.
u?v = u T Av
donde el lado derecho es la multiplicación de matriz habitual. Si A es la matriz de identidad, se recupera el producto de punto estándar. En la práctica, si Jab es el espacio de colores, no desea mezclar los componentes, por lo que se puede usar una matriz diagonal distinta de la matriz de identidad. Además, es posible que desee mantener la escala en y b sin cambios para que se conserve la medida de matiz. Por lo tanto, una variación útil del producto de punto euclidano estándar es la siguiente.
w J (componente J de usted)(componente J de v) + (un componente de usted)(un componente de v) + (componente b de usted)(componente b de v)
donde w J es un número positivo. Una variación adicional es permitir que w J varíe con el punto de consulta de entrada:
w J\ = w J (queryPoint)
El resultado final es una medida de distancia que es asimétrica con respecto a los dos puntos, y con diferentes pesos relativos sobre la ligereza y el color o matiz a medida que el punto de consulta de entrada varía. Esto está de acuerdo con algunas observaciones sobre la percepción del color humano de que las diferencias de color no se ponderan igualmente en todas las dimensiones. Se ha encontrado que las personas son menos sensibles a las diferencias de ligereza que las diferencias en el matiz y el cromático.
La siguiente función de peso es útil.
w J = k ₓ k ₁ (C - C mₐₓ ) n
donde k ₐ = 1, k ₁ = 0,75/(C mₐₓ ) n, C mₐₓ = 100, n = 2 y C es el menor de cromática del punto de consulta y C mₐₓ.
para que un peso de 0,25 se ponga en el término J cuando el cromático es cero, y un peso de 1 cuando el cromático es 100. La tendencia de poner menos peso en J cuando el cromático es pequeño, y más peso en J cuando el cromático es grande sigue el uso recomendado para CMC y CIEDE2000.
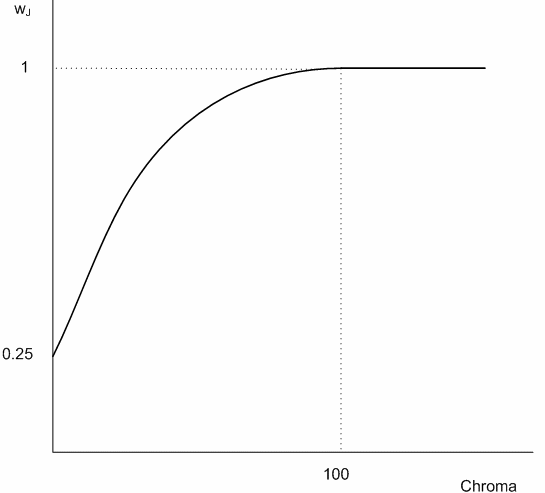
Figura 31 : Función de peso en el componente J de la métrica
Use el espacio Jab para el ejemplo siguiente. Es muy exigente a nivel computacional buscar en todos los triángulos de límite para determinar el punto más cercano de la métrica euclidiana. A continuación se muestra un enfoque sencillo para hacer que este proceso sea lo más eficaz posible, sin introducir suposiciones adicionales que puedan acelerar el proceso, sino que también terminan en una respuesta aproximada. En primer lugar, es necesario comprender el procedimiento geométrico de proyectar un punto en el triángulo especificado. Aquí se ofrece una descripción.
Primero se realiza una proyección ortogonal en el plano infinito que contiene el triángulo. La distancia más corta del punto de consulta desde el plano se puede determinar en dos pasos.
(a) Calcule el vector normal de unidad en el triángulo.
(b) Calcule el producto de punto del vector normal unitario y un vector formado desde el punto de consulta y un punto en el triángulo; es decir, uno de sus vértices. Dado que el vector normal tiene longitud de unidad, el valor absoluto de este producto de punto es la distancia del punto de consulta desde el plano.
Es posible que el punto proyectado no sea la respuesta, porque podría estar fuera del triángulo. Por lo tanto, primero debe realizar una comprobación. El cálculo es equivalente a calcular las coordenadas barycéntricas del punto proyectado en relación con el triángulo. Si se determina que el punto proyectado está dentro del triángulo, es la respuesta. Si no es así, el punto más cercano se adquiere en uno de los bordes del triángulo. Realice una búsqueda en cada uno de los tres bordes. Determinar la proyección del punto de consulta en un borde es un proceso similar a la proyección en el triángulo, pero una dimensión menor. Primero se calcula una proyección ortogonal. Si el punto proyectado se encuentra en el borde, es la respuesta. Si no es así, el punto más cercano se adquiere en uno de los dos puntos finales. Realizar una búsqueda en los dos puntos finales; es decir, calcule la distancia del punto de consulta de cada uno y compare cuál es menor.
Un examen cuidadoso revela que hay una gran cantidad de búsquedas repetidas al recorrer todos los triángulos porque un borde siempre se comparte por dos triángulos y un vértice compartido por al menos tres bordes. Además, no te interesa encontrar el punto más cercano a un triángulo en particular; en su lugar, está interesado en encontrar el punto más cercano al límite de gama completa. Sin embargo, un triángulo determinado sería el en el que se logra esto. Hay dos estrategias que puede usar para acelerar la búsqueda.
Estrategia I. Cada vértice se procesará, como máximo, una vez. Cada borde se procesará, como máximo, una vez.
Estrategia II. En cualquier momento de la búsqueda, tiene un mejor candidato con la mejor distancia correspondiente. Si puede determinar, mediante una comprobación rápida, que un triángulo no es capaz de dar una mejor distancia, no es necesario continuar el cálculo más allá. No necesita el punto y la distancia más cercanos para este triángulo.
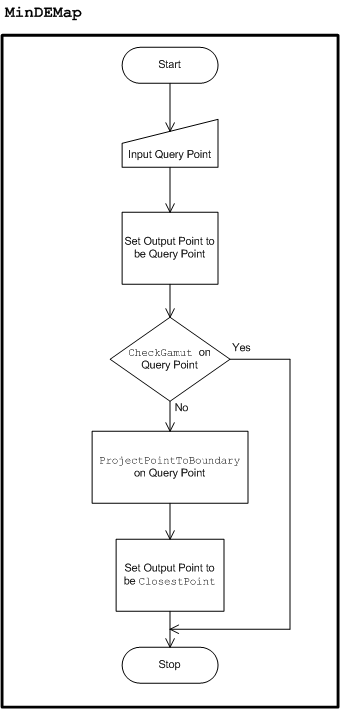
Figura 32 : Esquemas mínimos de asignación de DE
En la figura 32 se muestra el flujo general de lógica para el mapa de gama MinDEMap. Para un punto de consulta, primero se invoca la función CheckGamut. Si el punto está en gamut, el mapa es una operación sin operación. Si el punto está fuera de gama, llame a ProjectPointToBoundary. Ahora pase a la figura 33. En este momento, se supone que se han calculado los siguientes valores.
(a) Vector normal unitario a cada triángulo de límite de gama con respecto al producto de puntos estándar.
(b) Lista de vértices y lista de bordes, además de la lista de triángulos.
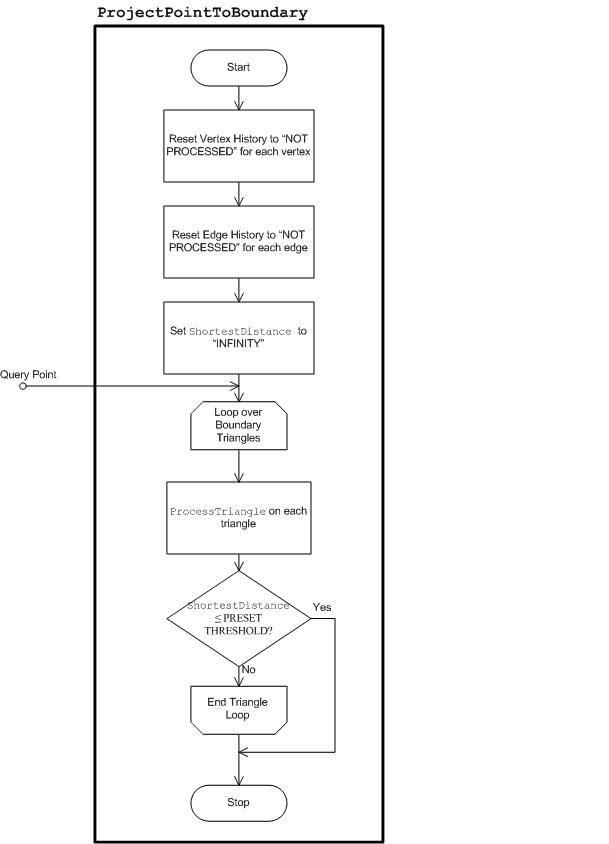
Figura 33 : Rutina ProjectPointToBoundary
Todas estas son sobrecargas constantes y habrían disminuido el costo si se realizan suficientes consultas a este límite de gama. Normalmente, este es el caso cuando se crea una transformación LUT de un dispositivo a otro, donde solo hay dos gamas fijas y la transformación LUT se ejecuta a través de puntos en la cuadrícula de muestreo uniforme. Calcule previamente los vectores normales con respecto al producto de punto estándar, aunque la noción de perpendicularidad se basará en el producto de punto ponderado, que depende del punto de consulta, tal como se explicó anteriormente. La razón se debe a que un vector normal con respecto al producto de puntos ponderados se puede obtener fácilmente del vector normal con respecto al producto de punto estándar. Si n ₀ es un vector normal con respecto al producto de punto estándar, entonces
n = (componente J de n ₀ /w J, a-component of n ₀, b-component of n ₀ )
es normal para el triángulo con respecto al producto de punto ponderado. Debido a esta relación, sigue siendo beneficioso calcular previamente n ₀ aunque se deba ajustar en función del punto de consulta.
La rutina ProjectPointToBoundary comienza restableciendo el "historial procesado" de los vértices y bordes. Se trata de tablas de marcas BOOLEAN que realizan un seguimiento de si se ha visitado un vértice o borde antes. También restablece la variable ShortestDistance a "INFINITY", que es el valor máximo codificado en el sistema de números de punto flotante usado. A continuación, se ejecuta a través de un bucle, buscando el punto más cercano de cada triángulo mediante la llamada ProcessTriangle. ProcessTriangle es la rutina para actualizar la variable ShortestDistance y está claramente en el bucle crítico. Una optimización es detener cuando el resultado es lo suficientemente bueno. Después de cada llamada a ProcessTriangle, se examina la variable ShortestDistance. Si satisface un umbral predefinido, puede detenerse. El umbral predefinido depende del espacio de colores utilizado y de la precisión necesaria del sistema de creación de imágenes de color. Para una aplicación típica, no desea realizar un trabajo innecesario si la diferencia de color es menor que lo que la visión humana puede distinguir. Para CIECAM02, esta diferencia de color es 1. Use un valor de umbral de 0,005 en la implementación, sin embargo, para conservar la precisión de los cálculos, ya que esto podría ser solo un paso intermedio en una cadena de transformaciones.
ProcessTriangle implementa la estrategia II anterior. Obtener un vector normal del vector normal de la unidad preprocesada al triángulo con respecto al producto de punto estándar, calcula la distancia del punto de consulta al plano infinito que contiene el triángulo formando el producto de punto del vector normal de unidad y queryVector, el vector de uno de los vértices del triángulo, vértice1, al punto de consulta, queryPoint.
queryVector = queryPoint - vertex1
distance = | normalVector * queryVector |/|| normalVector||
Se trata de un cálculo relativamente económico y la distancia es necesaria para realizar cálculos adicionales. Si esta distancia no es menor que la mejor distancia actual, ShortestDistance, este triángulo no producirá una mejor distancia, ya que no dará una mejor distancia que el plano que lo contiene. En este caso, se devuelve el control al bucle de triángulos. Si la distancia es menor que ShortestDistance, potencialmente, tiene un punto más cercano, si este punto se encuentra dentro del triángulo. Debe realizar algunos cálculos "duros" (aunque nada más allá del álgebra lineal) para determinarlo. Si los otros dos vértices del triángulo son vértices2 y vértices3, forman primero los vectores baseBasisVector y secondBasisVector.
firstBasisVector = vertex2 - vertex1
secondBasisVector = vertex3 - vertex1
Use el siguiente sistema lineal de ecuaciones para resolver los desconocidos que usted y v.
firstBasisVector * queryVector = (firstBasisVector * firstBasisVector)u + (firstBasisVector * secondBasisVector)v
secondBasisVector * queryVector = (secondBasisVector * firstBasisVector)u + (secondBasisVector * secondBasisVector)v
y las condiciones para que el punto proyectado se encuentre dentro del triángulo son:
0 ≤ u ≤ 1, 0 ≤ v ≤ 1 y usted + v ≤ 1
Después de este cálculo, si se determina que el punto proyectado se encuentra dentro del triángulo, ha encontrado un nuevo punto más cercano; la distancia que calculó al principio es la distancia más corta. En este caso, actualice las variables ShortestDistance y ClosestPoint. Si el punto proyectado se encuentra fuera del triángulo, es posible que encuentre un punto más cercano en uno de sus bordes. Por lo tanto, puede llamar a la rutina ProcessEdge en cada uno de los tres bordes.
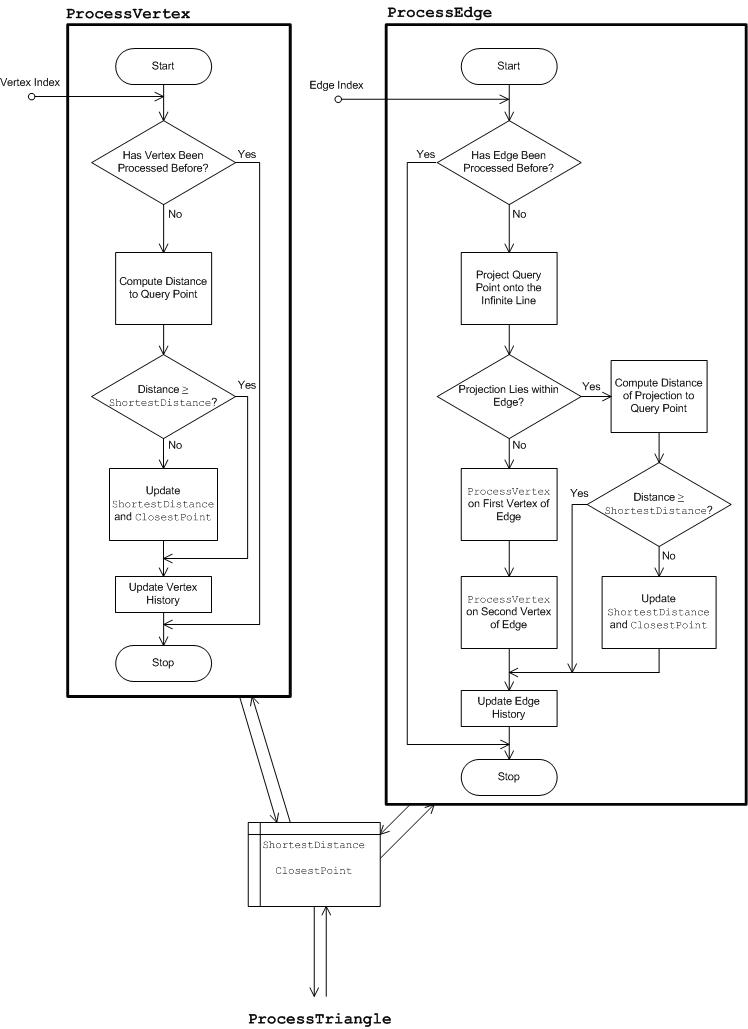
Figura 34 : Rutinas ProcessEdge y ProcessVertex
La rutina ProcessEdge implementa la estrategia I, que se muestra en la figura 34. ProcessEdge se inicia comprobando si el borde se ha procesado antes. Si es así, no se realiza ninguna otra acción. Si no es así, continúa calculando la proyección ortogonal del punto de consulta en la línea infinita que contiene el borde. El álgebra lineal implicada en el cálculo es similar a las ecuaciones de triángulo anteriores. Sin embargo, el cálculo es más sencillo, no se describe aquí. Si el punto proyectado se encuentra dentro del borde, encontrará la distancia del punto proyectado desde el punto de consulta. Si esta distancia es menor que ShortestDistance, ha encontrado un nuevo punto más cercano. Actualice ShortestDistance y ClosestPoint. Si el punto proyectado se encuentra fuera del borde, llame a ProcessVertex en los dos puntos finales. Antes de devolver el control, actualice el historial de bordes para que este borde se marque como "PROCESSED".
Por último, proporcione una descripción de ProcessVertex. La rutina ProjectVertex también implementa la estrategia I y mantiene una tabla de historial de vértices. Como se muestra en la figura 34, primero comprueba si el vértice se ha procesado antes. Si es así, no se realiza ninguna otra acción. Si no es así, continúa calculando la distancia del vértice desde el punto de consulta. Si la distancia es menor que ShortestDistance, actualice ShortestDistance y ClosestPoint. Al final, actualiza el historial de vértices para que este vértice se marque como "PROCESADO".
Cuando el bucle de control externo ha agotado todos los triángulos o ha salido antes de que se alcance el umbral de diferencia de color, se obtiene acceso a la variable ClosestPoint. Este es el resultado de MinDEMap. El autor de la llamada también puede recuperar ShortestDistance si está interesado en cuánto se encuentra el color asignado del color de la consulta.
Suavizado de matiz
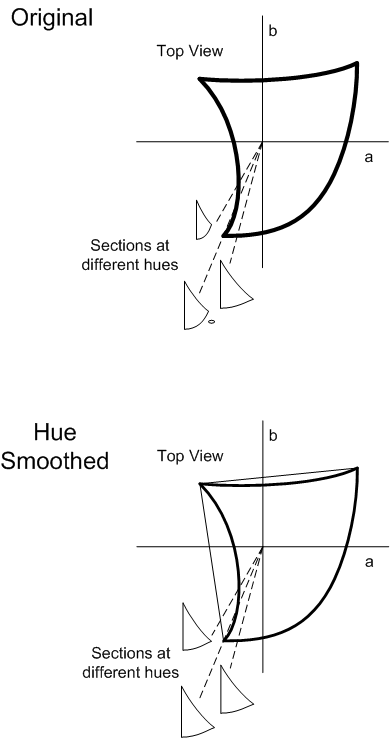
Figura 35 : Suavizado de matiz
Surge un problema con las operaciones restringidas de matiz; Es decir, la operación solo tiene en cuenta las variables dentro de un plano de matiz. En la figura 35 se muestra un ejemplo de una gama que muestra segmentos de matiz "discontinuos" en los tonos azules. Dentro de este intervalo de matiz, para ciertos ángulos de matiz, el límite de la gama es tangencial al plano de matiz. En efecto, esto provoca un cambio en la estructura topológica de los segmentos de matiz. En el ejemplo que se muestra, a medida que el plano de matiz recorre este intervalo de matiz, surge una "isla" y se sumergió. Este cambio en la topología hará que las operaciones específicas de matiz sean discontinuas. Por ejemplo, la cusp en el matiz fijo cambiará abruptamente a medida que el ángulo de matiz cambia a través de este rango.
Hay una razón de ciencia de colores por la que es conveniente conservar el matiz en determinadas operaciones. Para resolver el problema anterior, los triángulos de límite de gamut originales deben ser "suavizados de matiz". Por lo general, un suavizado de matiz de un conjunto de triángulos de límites de gamut es un conjunto de triángulos de forma que (a) forma el límite de una nueva "gama", que podría no corresponder a la gama de dispositivos real, y que contiene la gama definida por el conjunto original de triángulos; y (b) los triángulos del nuevo conjunto se delimitan lejos de ser paralelos a los planos de matiz.
Una manera práctica de obtener un conjunto suavizado de tonos de triángulos es tomar el casco convexa de los vértices originales. Como se muestra en la figura 35, los segmentos de matiz del casco convexa varían suavemente en el rango de matiz problemático sin un cambio repentino en la topología.
Establecer elementos primarios y secundarios en la descripción del límite de gama
Algunos métodos de asignación de gama, como HueMap, dependen de la ubicación de los dispositivos principales y secundarias. Para los dispositivos aditivos, los principales son rojo, verde y azul (R, G y B); y las secundarias son cian, magenta y amarillo (C, M e Y). En el caso de los dispositivos restivos, los principales son C, M e Y; y las secundarias son R, G y B. El GBD realiza un seguimiento de los seis valores, además de blanco y negro (W y K), en una matriz de valores de color Jab. Estos valores se establecen en la descripción del límite de gama cuando se crea. En el caso de los dispositivos de salida, las principales se pueden determinar mediante la ejecución de combinaciones de valores de control de dispositivo a través del modelo de dispositivo. En el caso de los dispositivos de captura, este enfoque no es adecuado para crear el GBD de referencia, ya que es casi imposible capturar una imagen que produce un valor de dispositivo puro totalmente saturado, como (0,0, 0,0, 1,0). Los perfiles de dispositivo WCS contienen los índices de las principales en el destino de captura. Dado que estos valores no están contenidos en un perfil ICC, utilice valores medidos a partir de un objetivo típico del escáner después de convertir en Jab, en relación con las condiciones de visualización de ICC.
Establecer el eje neutro en la descripción del límite de gama
Los métodos de asignación de gama MinCD y HueMap y Relative MinCD usan el eje neutro del dispositivo para enderezar. Para los dispositivos de salida de línea base, el eje neutro se puede determinar ejecutando valores neutros del dispositivo (R=G=B o C=M=Y) a través del método DeviceToColorimetric y, a continuación, a través del método ColorimetricToAppearance del objeto CIECAM02. Sin embargo, los dispositivos de captura no siempre devuelven un valor neutro del dispositivo cuando se presenta una muestra neutra. Esto es especialmente cierto cuando la iluminación ambiental no es perfectamente neutra. Los perfiles de dispositivo WCS contienen los índices de las muestras neutras del destino. Use esos ejemplos para establecer el eje neutro. Dado que esta información no está disponible para los perfiles ICC, debe usar el mismo método que se usa para los dispositivos de salida; ejecute ejemplos neutros del dispositivo a través del método DeviceToColorimetric y, a continuación, adále los valores de entrada y los resultados de colorimetric.
Temas relacionados