Apéndice: Transformaciones de matriz
En este tema se proporciona información general matemática sobre las transformaciones de matriz para gráficos 2D. Sin embargo, no es necesario conocer las matemáticas de matriz para usar transformaciones en Direct2D. Lea este tema si está interesado en las matemáticas; de lo contrario, no dude en omitir este tema.
Introducción a matrices
Una matriz es una matriz rectangular de números reales. El orden de la matriz es el número de filas y columnas. Por ejemplo, si la matriz tiene 3 filas y 2 columnas, el orden es 3 × 2. Normalmente, las matrices se muestran con los elementos de matriz entre corchetes:
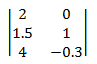
Notación: una matriz se designa mediante una letra mayúscula. Los elementos se designan mediante letras minúsculas. Los subíndices indican el número de fila y columna de un elemento. Por ejemplo, unij es el elemento de la columna i'th row y j'th de la matriz A.
En el diagrama siguiente se muestra una matriz i × j, con los elementos individuales de cada celda de la matriz.

Operaciones de matriz
En esta sección se describen las operaciones básicas definidas en matrices.
Adición. La suma A + B de dos matrices se obtiene agregando los elementos correspondientes de A y B:
- A + B = \[ a*ij* \] + \[ b*ij* \] = \[ a*ij* + b*ij* \]
Multiplicación escalar. Esta operación multiplica una matriz por un número real. Dado un número real k, el producto escalar kA se obtiene multiplicando cada elemento de A por k.
- kA = k\[ a*ij* \] = \[ k × a*ij* \]
Multiplicación de matriz. Dadas dos matrices A y B con orden (m × n) y (n × p), el producto C = A × B es una matriz con orden (m × p), definido de la siguiente manera:
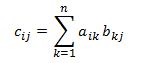
o, de forma equivalente:
- c*ij* = a*i*1 x b1*j* + a*i*2 x b2*j* + ... + a*in* + b*nj*
Es decir, para calcular cada elementocij, haga lo siguiente:
- Tome la fila I'ésima de A y la columna j'th de B.
- Multiplique cada par de elementos de la fila y columna: la primera entrada de fila por la primera entrada de columna, la segunda entrada de fila por la segunda entrada de columna, etc.
- Suma el resultado.
Este es un ejemplo de multiplicar una matriz (2 × 2) por una matriz (2 × 3).
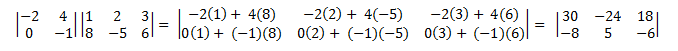
La multiplicación de matriz no es conmutativa. Es decir, A × B ≠ B × A. Además, a partir de la definición, sigue que no se pueden multiplicar todos los pares de matrices. El número de columnas de la matriz izquierda debe ser igual al número de filas de la matriz derecha. De lo contrario, el operador × no está definido.
Identificar matriz. Una matriz de identidad, designada I, es una matriz cuadrada definida de la siguiente manera:
- I*ij* = 1 si *i* = *j*, o 0 de lo contrario.
En otras palabras, una matriz de identidad contiene 1 para cada elemento donde el número de fila es igual al número de columna y cero para todos los demás elementos. Por ejemplo, esta es la matriz de identidades 3 × 3.
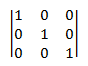
Las siguientes igualdades contienen para cualquier matriz M.
- M x I = M I x M = M
Transformaciones Affine
Una transformación afín es una operación matemática que asigna un espacio de coordenadas a otro. En otras palabras, asigna un conjunto de puntos a otro conjunto de puntos. Las transformaciones Affine tienen algunas características que las hacen útiles en los gráficos informáticos.
- Las transformaciones Affine conservan la collinearidad. Si tres o más puntos se encuentran en una línea, todavía forman una línea después de la transformación. Las líneas rectas permanecen rectas.
- La composición de dos transformaciones afín es una transformación afín.
Las transformaciones Affine para el espacio 2D tienen la siguiente forma.
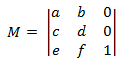
Si aplica la definición de multiplicación de matriz dada anteriormente, puede mostrar que el producto de dos transformaciones affine es otra transformación afín. Para transformar un punto 2D mediante una transformación afín, el punto se representa como una matriz de 1 × 3.
- P = \| x y 1 \|
Los dos primeros elementos contienen las coordenadas x e y del punto. El 1 se coloca en el tercer elemento para que las matemáticas funcionen correctamente. Para aplicar la transformación, multiplique las dos matrices de la siguiente manera.
- P' = P × M
Esto se expande a lo siguiente.
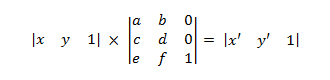
where
- x' = ax + cy + e y' = bx + dy + f
Para obtener el punto transformado, tome los dos primeros elementos de la matriz P'.
- p = (x', y') = (ax + cy + e, bx + dy + f)
Nota
Una matriz de 1 × n se denomina vector de fila. Direct2D y Direct3D usan vectores de fila para representar puntos en el espacio 2D o 3D. Puede obtener un resultado equivalente mediante un vector de columna (n × 1) y transponer la matriz de transformación. La mayoría de los textos gráficos usan la forma vectorial de columna. En este tema se presenta el formato vectorial de fila para la coherencia con Direct2D y Direct3D.
En las siguientes secciones se derivan las transformaciones básicas.
Transformación de traducción
La matriz de transformación de traducción tiene el siguiente formato.
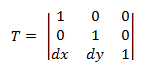
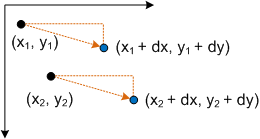
Conectar un punto P a esta ecuación produce:
- P' = (*x* + *dx*, *y* + *dy*)
que corresponde al punto (x, y) traducido por dx en el eje X y dy en el eje Y.
Transformación de escalado
La matriz de transformación de escalado tiene el siguiente formato.
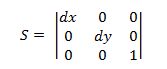
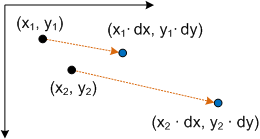
Conectar un punto P a esta ecuación produce:
- P' = (*x* * * * *dx*, *y* ** *dy*)
que corresponde al punto (x,y) escalado por dx y dy.
Rotación alrededor del origen
La matriz para girar un punto alrededor del origen tiene el siguiente formato.
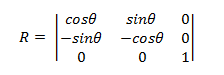
El punto transformado es:
- P' = (*x*cosΘ – ysinΘ, *x*sinΘ + *y*cosΘ)
Prueba. Para mostrar que P' representa una rotación, tenga en cuenta el siguiente diagrama.
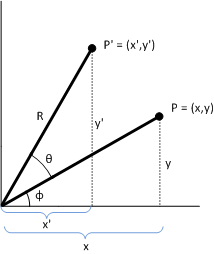
Con estas premisas:
-
P = (x,y)
-
Punto original que se va a transformar.
-
Φ
-
Ángulo formado por la línea (0,0) a P.
-
Θ
-
Ángulo por el que se va a girar (x,y) sobre el origen.
-
P' = (x',y')
-
Punto transformado.
-
R
-
Longitud de la línea (0,0) a P. También el radio del círculo de rotación.
Nota
En este diagrama se usa el sistema de coordenadas estándar usado en geometry, donde el eje Y positivo apunta hacia arriba. Direct2D usa el sistema de coordenadas de Windows, donde el eje Y positivo apunta hacia abajo.
El ángulo entre el eje x y la línea (0,0) a P' es Ν + Θ. Las identidades siguientes contienen:
- x = R cosΝ y = R sinΝ x' = R cos(Ν + Θ) y' = R sin(Ν+ Θ)
Ahora resuelve x' e y' en términos de Θ. Por las fórmulas de suma trigonométrica:
- x' = R(cosΝcosΘ – sinΝsinΘ) = RcosΝcosΘ – RsinΝsinΘ y' = R(sinΝcosΘ + cosΝsinΘ) = RsinΝcosΘ + RcosΝsinΘ
Sustituyendo, obtenemos:
- x' = xcosΘ – ysinΘ y' = xsinΘ + ycosΘ
que corresponde al punto transformado P' mostrado anteriormente.
Rotación alrededor de un punto arbitrario
Para girar alrededor de un punto (x,y) distinto del origen, se usa la siguiente matriz.
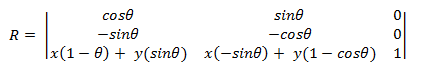
Puede derivar esta matriz tomando el punto (x,y) como origen.
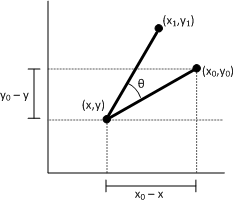
Let (x1, y1) ser el punto resultante de girar el punto (x0, y0) alrededor del punto (x,y). Podemos derivar x1 como se indica a continuación.
- x1 = (x0 – x)cosΘ– (y0 – y)sinΘ + x1 = x0cosΘ – y0sinΘ + \[ (1 – cosΘ) + ysinΘ \]
Ahora, vuelva a conectar esta ecuación a la matriz de transformación, usando la fórmula x1 = ax0 + cy0 + e de versiones anteriores. Use el mismo procedimiento para derivar y1.
Transformación de asimetría
La transformación de asimetría se define mediante cuatro parámetros:
- Θ: La cantidad que se va a sesgar a lo largo del eje X, medida como un ángulo del eje Y.
- Ν: La cantidad que se va a sesgar a lo largo del eje Y, medida como un ángulo del eje X.
- (px, py): coordenadas x e y del punto sobre el que se realiza la asimetría.
La transformación de asimetría usa la siguiente matriz.
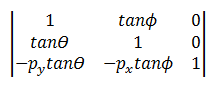
El punto transformado es:
- P' = (*x* + *y*tanΘ – *py*tanΘ, *y* + *x*tanΝ) – *py*tanΝ
o de forma equivalente:
- P' = (*x* + (*y* – *py*)tanΘ, *y* + (*x* – *px*)tanΝ)
Para ver cómo funciona esta transformación, considere cada componente individualmente. El parámetro Θ mueve cada punto en la dirección x por una cantidad igual a tanΘ. En el diagrama siguiente se muestra la relación entre Θ y la asimetría del eje X.
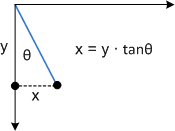
Este es el mismo sesgo aplicado a un rectángulo:
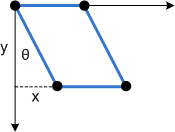
El parámetro Ν tiene el mismo efecto, pero a lo largo del eje Y:
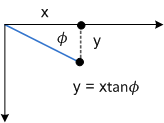
En el diagrama siguiente se muestra la asimetría del eje Y aplicada a un rectángulo.
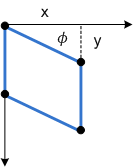
Por último, los parámetros px y py desplazan el punto central del sesgo a lo largo de los ejes x e y.
Representar transformaciones en Direct2D
Todas las transformaciones de Direct2D son transformaciones afín. Direct2D no admite transformaciones no afín. Las transformaciones se representan mediante la estructura D2D1_MATRIX_3X2_F . Esta estructura define una matriz de 3 × 2. Dado que la tercera columna de una transformación afín siempre es la misma ([0, 0, 1]) y porque Direct2D no admite transformaciones no afín, no es necesario especificar la matriz completa de 3 × 3. Internamente, Direct2D usa 3 matrices × 3 para calcular las transformaciones.
Los miembros del D2D1_MATRIX_3X2_F se denominan según su posición de índice: el miembro _11 es el elemento (1,1), el miembro _12 es el elemento (1,2), etc. Aunque puede inicializar directamente los miembros de la estructura, se recomienda usar la clase D2D1::Matrix3x2F . Esta clase hereda D2D1_MATRIX_3X2_F y proporciona métodos auxiliares para crear cualquiera de las transformaciones afín básicas. La clase también define operator*() para componer dos o más transformaciones, como se describe en Aplicar transformaciones en Direct2D.
Siguientes