Algoritmo de vector de cuaternión de orientación del dispositivo

En este artículo se describe el algoritmo que usa el Kit de laboratorio de hardware de Windows (Windows HLK) para determinar la diferencia entre el vector recibido y el vector esperado para la precisión de los datos del eje 9 en las pruebas avanzadas del sensor de orientación. Las pruebas comprueban que la fusión del sensor está correctamente integrada y que todos los sensores necesarios para la fusión del sensor se integran e instalan correctamente.

Nota

En algunos casos, puede usar la herramienta de diagnóstico del sensor para examinar el inclinómetro 3D y el sensor de orientación de dispositivo agregado que está bajo prueba.

Algoritmo de vector de cuaternión

El algoritmo usa las cos de arco del producto de punto dimensional 4 de los dos vectores, dividido por el producto de la magnitud de los dos vectores y dividido entre 2. Este algoritmo se muestra en la figura 1 Fórmula del algoritmo vectorial de cuaternión:

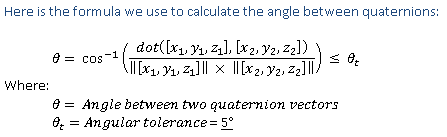
Los valores de matriz de rotación se convierten en valores de cuaternión para la validación de precisión. El vector de cuaternión calculado no debe desviarse más de +/- 5 grados del vector de cuaternión esperado (tolerancia en comparación con el ángulo formado entre vectores de cuaternión) (**+/- Precisión de 10 grados permitida en la dirección del eje de encabezado). La prueba HLK de Windows permite que el delta de Øt sea de hasta 15 grados.

Cómo calcular el ángulo delta entre los vectores de quaternion recibidos y esperados

En esta sección se describe el cálculo que calcula el ángulo delta entre los vectores de Quaternion recibidos y esperados en pruebas de orientación avanzada en HLK de Windows.

Los dos valores de datos siguientes son de interés en el informe de datos del sensor de orientación del dispositivo agregado:

• Vector de cuaternión

• Matriz de rotación

La prueba consta de las dos comprobaciones siguientes:

1. Comprobación del vector quaternion recibido en el informe de datos del sensor. Un vector quaternion tiene la forma (xi + yj + zk + w).

   1. Siempre se espera que el valor de w sea positivo.

   2. Se espera que el vector quaternion se normalice y no sea cero. Por ejemplo, la magnitud del vector debe estar cerca de 1,0. Se proporciona un porcentaje (1%) de margen para redondear los errores en el cálculo de la magnitud.

   3. El ángulo delta se calcula mediante delta = 2 * Acos( ( Exp . Rec ) / ( | Exp | * | Rec | ) ) , donde:

      \* indica la multiplicación escalar.

      . indica el producto de punto

      Exp es el vector quternion esperado

      Rec es el vector de cuaternión recibido.

      | Q |indica la magnitud del vector de quternion.

      delta es el ángulo en grados.

   4. Si delta es mayor que 360 grados, delta se vuelve a calcular como delta = delta - 360.

   5. En este momento, delta debe ser menor o igual que la tolerancia a errores; por ejemplo, 10 grados.

2. Comprobación de la matriz de rotación recibida. Se espera que la matriz de rotación sea una matriz de 3x3.

   1. Cada columna y vector de fila de la matriz de rotación se deben normalizar y no cero. Se proporciona un margen de margen (1) para redondear los errores en el cálculo de la magnitud.

   2. La matriz de rotación recibida se transforma en un vector de cuaternión.

   3. Se vuelven a usar todos los pasos de <a><e> de verificación (1).

Temas relacionados

Probar la funcionalidad del sensor con la herramienta de diagnóstico del sensor

Integración de sensores de movimiento y orientación