¿Qué es la regresión?
La regresión es una técnica de análisis de datos sencilla, común y muy útil, a menudo denominada coloquialmente "ajustar una línea". En su forma más simple, la regresión ajusta una línea recta entre una variable (característica) y otra (etiqueta). En formas más complicadas, la regresión puede encontrar relaciones no lineales entre una sola etiqueta y varias características.
Regresión lineal simple
La regresión lineal simple modela una relación lineal entre una sola característica y una etiqueta normalmente continua, lo que permite que la característica prediga la etiqueta. Es posible que tenga un aspecto similar a este:
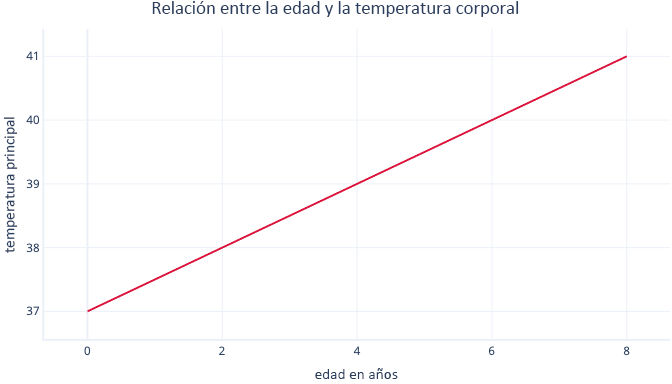
La regresión lineal simple tiene dos parámetros: una intersección (c), que indica el valor de la etiqueta cuando la característica se establece en cero, y una pendiente (m), que indica cuánto aumentará la etiqueta para cada incremento de un punto de la característica.
Si le gusta pensar matemáticamente, es muy simple:
y = mx + c
Donde y es la etiqueta y x es la característica.
Por ejemplo, en nuestro escenario, si intentamos predecir qué pacientes tendrán una temperatura corporal elevada en función de su edad, tendríamos el modelo:
temperatura = m * edad + c
Debe buscar los valores de m y c durante el procedimiento de ajuste. Si resulta que m = 0,5 y c = 37, es posible que lo visualicemos de la siguiente forma:
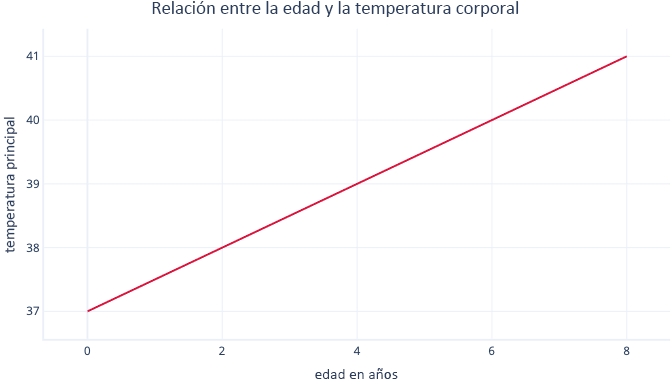
Esto significaría que cada año de edad está asociado con un aumento de la temperatura corporal de 0,5 °C, con un punto inicial de 37 °C.
Ajuste de la regresión lineal
Normalmente, usamos bibliotecas existentes para ajustarnos a los modelos de regresión. La regresión normalmente pretende encontrar la línea que genera el error mínimo, donde error se refiere a la diferencia entre el valor del punto de datos real y el valor previsto. Por ejemplo, en la imagen siguiente, la línea negra indica el error entre la predicción, la línea roja y un valor real: el punto.
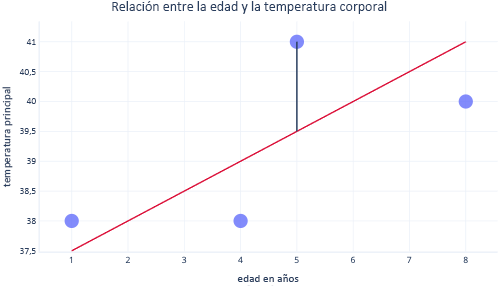
Al mirar estos dos puntos en un eje Y, podemos ver que la predicción era 39,5, pero el valor real era 41.
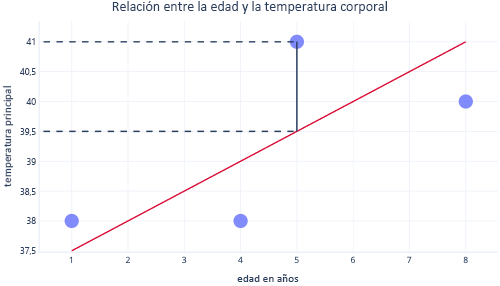
Por lo tanto, el modelo estaba equivocado en 1,5 para este punto de datos.
Normalmente, ajustamos un modelo minimizando la suma residual de cuadrados. Esto significa que la función de costo se calcula de la siguiente manera:
- Calcule la diferencia entre los valores reales y los previstos (como los anteriores) para cada punto de datos.
- Eleve estos valores al cuadrado.
- Sume (o halle el promedio) de estos valores al cuadrado.
El paso de elevar al cuadrado significa que no todos los puntos contribuyen uniformemente a la línea: los valores atípicos, que son puntos que no se encuentran en el patrón esperado, tienen un error desproporcionadamente mayor, lo que puede afectar la posición de la línea.
Puntos fuertes de la regresión
Las técnicas de regresión disponen de múltiples ventajas que otros modelos más complejos no tienen.
Predecible y fácil de interpretar
Las regresiones son fáciles de interpretar porque describen ecuaciones matemáticas simples, que a menudo se pueden representar en gráficos. Los modelos más complejos a menudo se conocen como soluciones de caja negra, porque es difícil comprender cómo hacen las predicciones o cómo se comportarán con determinadas entradas.
Fácil de extrapolar
Las regresiones hacen que sea fácil extrapolar: realizar predicciones para valores fuera del intervalo de nuestro conjunto de datos. Por ejemplo, es fácil calcular en el ejemplo anterior que un perro de nueve años tendrá una temperatura de 40,5 °C. Siempre se debe tener precaución a la hora de extrapolar: este modelo haría la predicción siguiente: a los 90 años se tendría una temperatura lo suficientemente alta como para hervir agua.
Normalmente, se garantiza un ajuste óptimo
La mayoría de los modelos de aprendizaje automático usan el trazo descendente del gradiente para ajustar los modelos, lo que implica el ajuste del algoritmo de trazo descendente del gradiente y no proporciona ninguna garantía de que se encontrará una solución óptima. Por el contrario, la regresión lineal que usa la suma de los cuadrados como función de costo no necesita realmente un procedimiento de trazo de gradiente descendente iterativo. En su lugar, se pueden usar las matemáticas para calcular la ubicación óptima de la línea. Las matemáticas están fuera del ámbito de este módulo, pero es útil saber que (siempre que el tamaño de la muestra no sea demasiado grande) con la regresión lineal no se necesita especial atención al proceso de ajuste y que se garantiza la solución óptima.