Conceptos de red neuronal profunda

Completado

Antes de explorar cómo entrenar un modelo de Machine Learning de red neuronal profunda(DNN), consideremos lo que se intenta lograr. El aprendizaje automático está relacionado con la predicción de una etiqueta en función de algunas características de una observación determinada. En términos simples, un modelo de Machine Learning es una función que calcula y (la etiqueta) a partir de x (las características): f(x)=y.

Un ejemplo de clasificación simple

Por ejemplo, supongamos que la observación consta de algunas medidas de un pingüino.

Específicamente, las medidas son las siguientes:

• El largo del pico del pingüino.
• La profundidad del pico del pingüino.
• El largo de la aleta del pingüino.
• El peso del pingüino.

En este caso, las características (x) son un vector de cuatro valores, o bien, matemáticamente expresado, x=[x₁,x₂,x₃,x₄].

Imagine que la etiqueta que intenta predecir (y) es la especie del pingüino y que hay tres posibilidades de especie:

0. Adelia
1. Papúa
2. Barbijo

Este es un ejemplo de un problema de clasificación, en el que el modelo de Machine Learning debe predecir la clase más probable a la que pertenece la observación. Un modelo de clasificación logra esto mediante la predicción de una etiqueta que consta de la probabilidad de cada clase. Es decir, y es un vector de valores de tres probabilidades, una para cada una de las posibles clases: y=[P(0),P(1),P(2)].

Puede entrenar el modelo de Machine Learning con las observaciones para las que ya conoce la etiqueta verdadera. Por ejemplo, puede tener las medidas de características siguientes para un pingüino de Adelia:

x=[37.3, 16.8, 19.2, 30.0]

Ya sabe que se trata de un ejemplo de un pingüino de Adelia (clase 0), por lo que una función de clasificación perfecta debe dar como resultado una etiqueta que indique una probabilidad del 100 % para la clase 0 y una probabilidad del 0 % para las clases 1 y 2:

y=[1, 0, 0]

Un modelo de red neuronal profunda

Por tanto, ¿cómo podríamos usar el aprendizaje profundo para crear un modelo de clasificación para el modelo de clasificación de los pingüinos? Veamos un ejemplo:

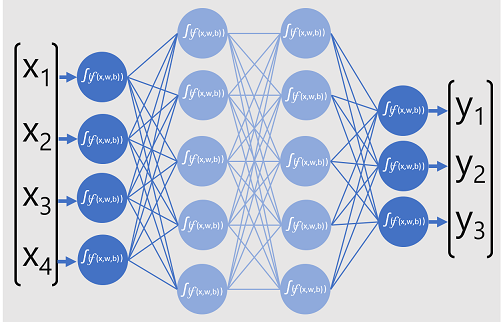
El modelo de red neuronal profunda para el clasificador consta de varias capas de neuronas artificiales. En este caso, hay cuatro capas:

• Una capa de entrada con una neurona para cada valor de entrada esperado (x).
• Dos capas denominadas ocultas, cada una con cinco neuronas.
• Una capa de salida con tres neuronas, una para cada valor de probabilidad de clase (y) que el modelo va a predecir.

Debido a la arquitectura en capas de la red, este tipo de modelo se conoce a veces como perceptrón de varias capas. Además, tenga en cuenta que todas las neuronas de las capas de entrada y ocultas están conectadas a todas los neuronas de las capas subsiguientes. Este es un ejemplo de una red totalmente conectada.

Al crear un modelo como este, debe definir un capa de entrada que admita la cantidad de características que va a procesar el modelo y una capa de salida que refleje la cantidad de salidas que espera que genere. Puede decidir la cantidad de capas ocultas que quiere incluir y cuántas neuronas en cada una de ellas, pero no tiene ningún control sobre los valores de entrada y salida de estas capas, ya que se determinan mediante el proceso de entrenamiento del modelo.

Entrenamiento de una red neuronal profunda

El proceso de entrenamiento de una red neuronal profunda se compone de varias iteraciones, llamadas épocas. Para la primera época, empiece por asignar valores de inicialización aleatorios para los valores de ponderación (w) y sesgo b. Luego, el proceso es tal como se muestra a continuación:

1. Las características de las observaciones de datos con valores de etiqueta conocidos se envían a la capa de entrada. Por lo general, estas observaciones se agrupan en lotes (que se suelen denominar como mini lotes).
2. Luego, las neuronas aplican su función y, si está activada, pasan el resultado a la capa siguiente hasta que la capa de salida genera una predicción.
3. La predicción se compara con el valor conocido real y se calcula el monto de la varianza entre los valores previstos y los verdaderos (lo que se conoce como la pérdida).
4. En función de los resultados, se calculan los valores revisados de os valores de ponderación y sesgo a fin de reducir la pérdida y estos ajustes se retropropagan a la neuronas de las capas de la red.
5. En la época siguiente, el entrenamiento por lotes se repite con propagación hacia adelante con los valores de ponderación y sesgo corregidos, a fin de mejorar la precisión del modelo (mediante la reducción de la pérdida).

Nota:

El procesamiento de las características de entrenamiento como un lote mejora la eficacia del proceso de entrenamiento mediante el procesamiento de varias observaciones de manera simultánea como una matriz de características con vectores de ponderaciones y sesgos. Las funciones algebraicas lineales que trabajan con matrices y vectores también se usan en el procesamiento de gráficos 3D. Como resultado, los equipos con unidades de procesamiento gráfico (GPU) ofrecen un rendimiento significativamente mejor para entrenar modelos de aprendizaje profundo que los equipos que solo tienen CPU (unidad de procesamiento central).

Una visión más detallada de las funciones de pérdida y la retropropagación

En la descripción anterior del proceso de entrenamiento de aprendizaje profundo se mencionó que la pérdida del modelo se calcula y utiliza para ajustar los valores de ponderación y sesgo. ¿Cómo funciona esto exactamente?

Cálculo de la pérdida

Supongamos que uno de los ejemplos transmitidos a través del proceso de entrenamiento contiene las características de un pingüino de Adelia (clase 0). La salida correcta de la red sería [1, 0, 0]. Ahora, supongamos que la red genera la salida [0.4, 0.3, 0.3]. Si las comparamos, podemos calcular una varianza absoluta para cada elemento (es decir, la distancia entre cada valor previsto y el valor que debería ser) como [0.6, 0.3, 0.3].

Dado que en la práctica se procesan varias observaciones, generalmente se agrega la varianza, por ejemplo, elevando cada valor de varianza a la potencia de 2 y luego calculando la media para terminar con un solo valor de pérdida promedio, como 0,18.

Optimizadores

Ahora viene la parte inteligente. La pérdida se calcula con una función que opera en los resultados de la capa final de la red, que también es una función. La capa de red final funciona en las salidas de las capas anteriores, que también son funciones. Por tanto, todo el modelo, desde la capa de entrada hasta el cálculo de la pérdida, no es más que una gran función anidada. Las funciones tienen algunas características muy útiles, entre las que se incluyen las siguientes:

• Puede conceptualizar una función como una línea trazada si compara su salida con cada una de sus variables.
• Puede usar un cálculo diferencial para calcular la derivada de la función en cualquier punto con respecto a sus variables.

Tomemos la primera de estas funcionalidades. Podemos trazar la línea de la función para mostrar cómo se compara un valor de ponderación individual con la pérdida y marcar en esa línea el punto en el que el valor de ponderación actual coincide con el valor de pérdida actual.

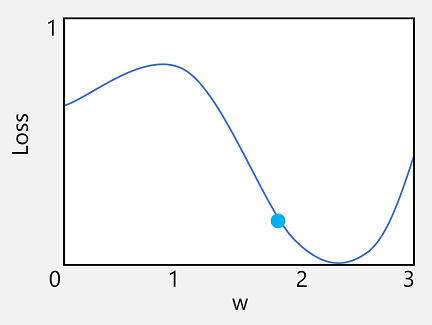
Ahora aplicaremos la segunda característica de una función. La derivada de una función para un punto determinado indica si la pendiente (o gradiente) de la salida de la función (en este caso, la pérdida) aumenta o disminuye con respecto a una variable de función (en este caso, el valor de ponderación). Una derivada positiva indica que la función está aumentando, mientras que una negativo indica que disminuye. En este caso, en el punto trazado del valor de ponderación actual, la función tiene una gradiente descendente. En otras palabras, el aumento de la ponderación disminuirá la pérdida.

Usamos un optimizador para aplicar este mismo truco a todas las variables de ponderación y sesgo del modelo y determinar en qué dirección se deben ajustar (hacia arriba o hacia abajo) para disminuir la cantidad total de pérdidas en el modelo. Hay varios algoritmos de optimización de uso común, que incluyen el descenso por gradiente estocástico (SGD), la tasa de aprendizaje adaptativo (ADADELTA) y la estimación de impulso adaptativo (Adam), entre otros; todos diseñados para determinar cómo ajustar las ponderaciones y los sesgos para reducir las pérdidas.

Velocidad de aprendizaje

Ahora, la siguiente pregunta obvia es: ¿cuánto debería ajustar el optimizador los valores de ponderaciones y sesgos? Si observa el trazado del valor de ponderación, puede ver que con un ligero aumento de la ponderación, la línea funcional cae (disminución de la pérdida). Sin embargo, si el valor aumenta demasiado, la línea de función comenzará a aumentar nuevamente y la pérdida puede incluso aumentar. Puede ser que después de la época siguiente resulte necesario disminuir la ponderación.

El tamaño del ajuste se controla mediante un parámetro que se establece para el entrenamiento, denominado velocidad de aprendizaje. Una velocidad de aprendizaje baja genera ajustes pequeños (por lo que puede tardar más épocas en minimizar la pérdida), mientras que una velocidad de aprendizaje alta genera ajustes grandes (de modo que es posible que no se alcance el mínimo).