Evaluación de diferentes tipos de agrupación en clústeres

Completado

Entrenamiento de un modelo de agrupación en clústeres

Hay varios algoritmos que puede usar para la agrupación en clústeres. Uno de los algoritmos más usados es la agrupación en clústeres k-means que, en su forma más sencilla, comprende los pasos siguientes:

1. Los valores de las características se vectorizan para definir coordenadas de n dimensiones (donde n es el número de características). En el ejemplo de la flor, hay dos características: número de pétalos y número de hojas. Por consiguiente, el vector de características tiene dos coordenadas que se pueden usar para trazar conceptualmente los puntos de datos en un espacio bidimensional.
2. Usted decide cuántos clústeres quiere usar para agrupar las flores: llame a este valor k. Por ejemplo, para crear tres clústeres, usaría un valor k de 3. Después, se representan los puntos k en coordenadas aleatorias. Estos puntos se convierten en los puntos centrales de cada clúster, por lo que se denominan centroides.
3. Cada punto de datos (en este caso, cada flor) se asigna a su centroide más cercano.
4. Cada centroide se mueve al centro de los puntos de datos asignados en función de la distancia media entre los puntos.
5. Si el centroide se mueve, los puntos de datos estarán más cerca de otro centroide, por lo que se reasignan a los clústeres en función del nuevo centroide más cercano.
6. Los pasos de movimiento de centroides y reasignación de clústeres se repiten hasta que los clústeres se estabilizan o se alcanza un número máximo predeterminado de iteraciones.

En la siguiente animación se ilustra este proceso:

Agrupación en clústeres jerárquica

La agrupación en clústeres jerárquica es otro tipo de algoritmo de agrupación en clústeres en el que los propios clústeres pertenecen a un grupos más grandes, que pertenecen a grupos incluso más grandes, y así sucesivamente. El resultado es que los puntos de datos pueden agruparse con diferentes grados de precisión: con un gran número de grupos muy pequeños y precisos, o con un pequeño número de grupos más grandes.

Por ejemplo, si aplicamos la agrupación en clústeres a los significados de las palabras, podemos obtener un grupo que contenga adjetivos específicos de las emociones ("enfadado", "feliz", etc.). Este grupo pertenece a un grupo que contiene todos los adjetivos relacionados con los humanos ("feliz", "guapo", "joven"), que pertenece a un grupo aún más alto que contiene todos los adjetivos ("feliz", "verde", "guapo", "duro", etc.).

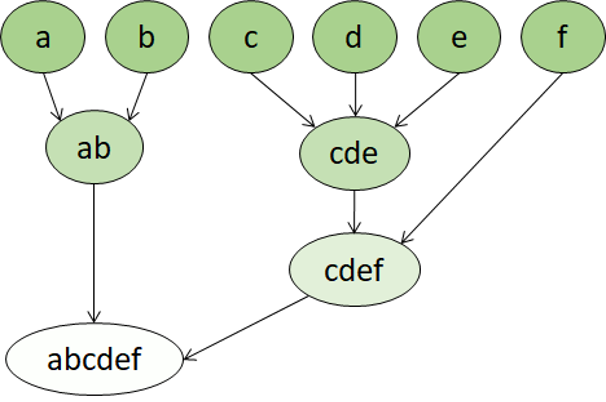
La agrupación en clústeres jerárquicas es útil no solo para dividir los datos en grupos, sino también para comprender las relaciones entre estos grupos. Una ventaja importante de la agrupación en clústeres jerárquica es que no requiere que se defina previamente el número de clústeres. Además, a veces, puede proporcionar resultados más interpretables que los enfoques no jerárquicos. El principal inconveniente es que estos enfoques pueden tardar más tiempo en calcularse que los enfoques más sencillos y, a veces, no son adecuados para grandes conjuntos de datos.