Evaluación de modelos de clasificación
La precisión del entrenamiento de un modelo de clasificación es mucho menos importante que lo bien que funcionará ese modelo cuando se le den nuevos datos no vistos. Después de todo, entrenamos modelos para que se puedan usar en los nuevos datos que se encuentran en el mundo real. Por lo tanto, después de entrenar un modelo de clasificación, evaluaremos cómo funciona con un conjunto de datos nuevos no vistos.
En las unidades anteriores, creamos un modelo que predecía si un paciente tenía diabetes o no en función de su nivel de glucosa en sangre. Ahora, cuando se aplica a algunos datos que no formaban parte del conjunto de entrenamiento, obtenemos las siguientes predicciones.
| x | y | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |
Recordemos que x se refiere al nivel de glucosa en sangre, y se refiere a si son realmente diabéticos, e ŷ se refiere a la predicción del modelo sobre si son diabéticos o no.
El simple cálculo de cuántas predicciones fueron correctas es a veces engañoso o demasiado simplista para que comprendamos el tipo de errores que cometerá en el mundo real. Para obtener información más detallada, podemos tabular los resultados en una estructura denominada matriz de confusión, como la siguiente:
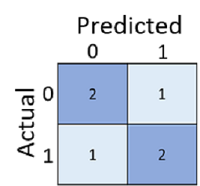
La matriz de confusión muestra el número total de casos en los que:
- El modelo predijo 0 y la etiqueta real es 0 (verdaderos negativos; arriba a la izquierda)
- El modelo predijo 1 y la etiqueta real es 1 (verdaderos positivos, abajo a la derecha)
- El modelo predijo 0 y la etiqueta real es 1 (falsos negativos, abajo a la izquierda)
- El modelo predijo 1 y la etiqueta real es 0 (falsos positivos, arriba a la derecha)
Las celdas de una matriz de confusión se suelen sombrear para que los valores más altos tengan un sombreado más profundo. De este modo, resulta más fácil ver una tendencia diagonal fuerte de la parte superior izquierda a la inferior derecha, resaltando las celdas en las que el valor predicho y el valor real son los mismos.
A partir de estos valores principales, puede calcular un rango de otras métricas que pueden ayudarle a evaluar el rendimiento del modelo. Por ejemplo:
- Exactitud: (VP+VN)/(VP+VN+FP+FN): de todas las predicciones, ¿cuántas son correctas?
- Coincidencia: VP/(VP+FN): de todos los casos que son positivos, ¿cuántos detectó el modelo?
- Precisión: VP/(VP+FP): de todos los casos en los que el modelo predijo ser positivo, ¿cuántos realmente son positivos?