Comparación y optimización de curvas de ROC
Las curvas de características operativas del receptor (ROC) nos permiten comparar modelos entre sí y ajustar nuestro modelo seleccionado. Vamos a analizar cómo y por qué se realizan.
Ajuste de un modelo
El uso más obvio de una curva de ROC es elegir un umbral de decisión que proporcione el mejor rendimiento. Recuerde que nuestros modelos nos proporcionan probabilidades, como una probabilidad del 65 % de que la muestra sea un excursionista. El umbral de decisión es el punto por encima del cual se asigna verdadero (excursionista) a una muestra o por debajo del cual se le asigna false (árbol). Si nuestro umbral de decisión fuera del 50 %, el 65 % se asignaría a "verdadero" (excursionista). Sin embargo, si nuestro umbral de decisión fuera del 70 %, una probabilidad del 65 % sería demasiado pequeña y se asignaría a "falso" (árbol).
Hemos visto en el ejercicio anterior que, al construir una curva de ROC, solo se cambia el umbral de decisión y se evalúa el funcionamiento del modelo. Al hacerlo, podemos encontrar el umbral que proporciona los resultados óptimos.
Por lo general, no hay un solo umbral que proporcione la mejor tasa de verdaderos positivos (TPR) y la tasa de falsos positivos (FPR) más baja. Esto significa que el umbral óptimo depende de lo que se intente lograr. Por ejemplo, en nuestro escenario, es muy importante tener una tasa de verdaderos positivos alta, ya que si no se identifica un excursionista y se produce una avalancha, el equipo no sabrá rescatarle. Sin embargo, existe un inconveniente: si la tasa de falsos positivos es demasiado alta, el equipo de rescate puede enviarse repetidamente para rescatar a personas que simplemente no existen. En otras situaciones, la tasa de falsos positivos se considera más importante. Por ejemplo, la ciencia tiene una tolerancia baja para los resultados falsos positivos. Si la tasa de falsos positivos de experimentos científicos fuera mayor, habría una oleada interminable de notificaciones contradictorias y sería imposible distinguir lo real.
Comparación de modelos con AUC
Puede usar las curvas de ROC para comparar modelos entre sí, al igual que con las funciones de costo. La curva de ROC de un modelo muestra lo bien que funcionará para una variedad de umbrales de decisión. Al fin y al cabo, lo más importante de un modelo es qué rendimiento tendrá en el mundo real, donde solo hay un umbral de decisión. ¿Por qué, entonces, desearíamos comparar modelos con umbrales que nunca usaremos? Existen dos respuestas para esto.
En primer lugar, comparar curvas de ROC de maneras concretas es como realizar una prueba estadística que nos indique no solo que un modelo ha funcionado mejor en este conjunto de pruebas concreto, sino si es probable que siga teniendo un mejor rendimiento en el futuro. Esto está fuera del ámbito de este material de aprendizaje, pero merece la pena tenerlo en cuenta.
En segundo lugar, la curva de ROC muestra, hasta cierto punto, cómo depende el modelo de tener el umbral perfecto. Por ejemplo, si nuestro modelo solo funciona bien cuando tenemos un umbral de decisión de 0,9, pero muy por encima o por debajo de este valor, no es un buen diseño. Probablemente preferiríamos trabajar con un modelo que funcione razonablemente bien para varios umbrales, sabiendo que si los datos reales que encontramos son ligeramente diferentes a nuestro conjunto de pruebas, el rendimiento de nuestro modelo no se contraerá necesariamente.
¿Cómo se comparan las ROC?
La manera más fácil de comparar las ROC numéricamente es usar el área bajo la curva (AUC). Literalmente, se trata del área del gráfico que se encuentra por debajo de la curva. Por ejemplo, nuestro modelo perfecto del último ejercicio tiene una AUC de 1:
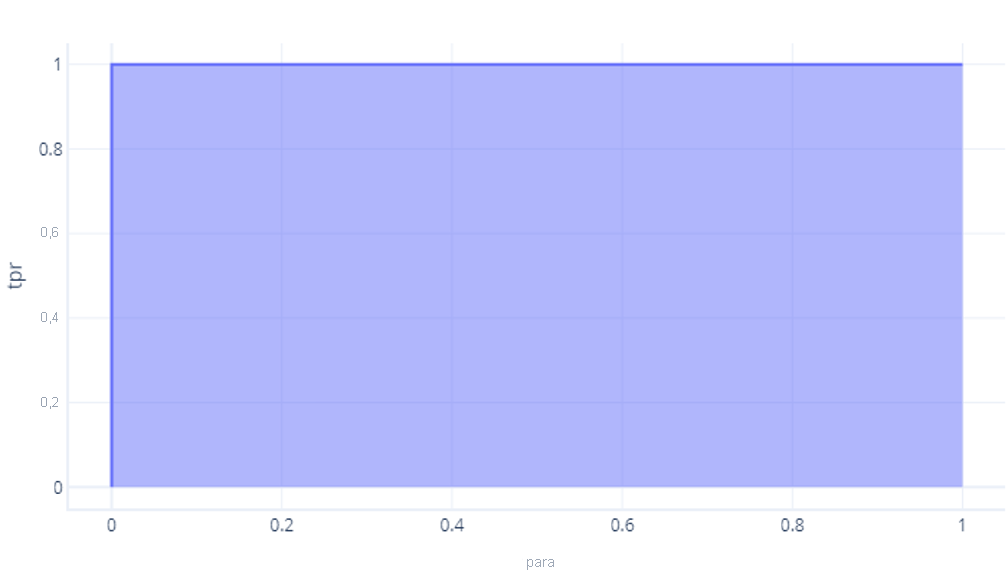
Aunque nuestro modelo cuyo rendimiento no era mejor al del simple azar tenga un área de aproximadamente 0,5:
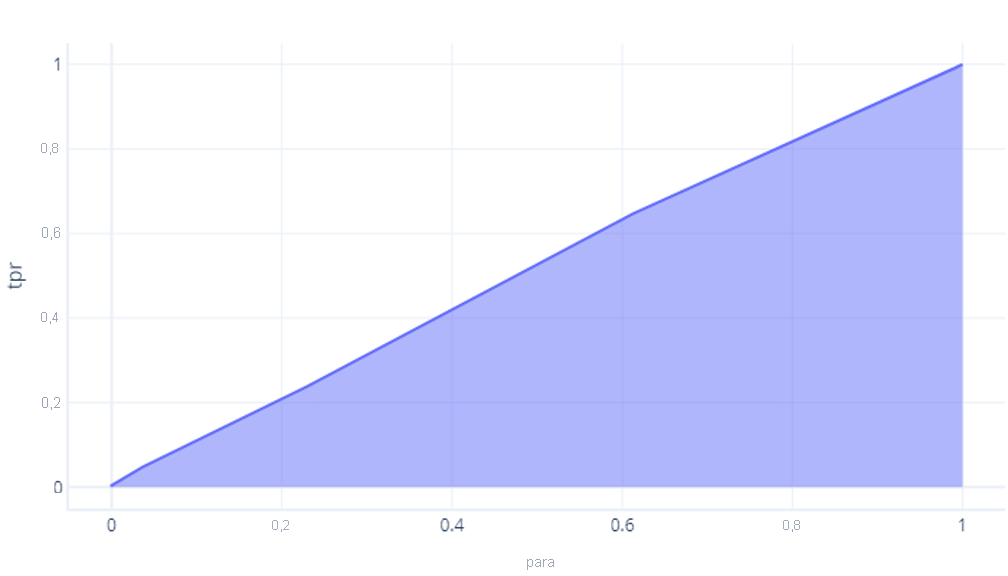
Cuanto más perfecto sea un modelo, mayor será esta área. Si tenemos un modelo con una AUC grande, sabemos que funciona bien para diversos umbrales, por lo que probablemente tiene una buena arquitectura y ha recibido un buen entrenamiento. Por el contrario, un modelo con una AUC pequeña (más próxima a 0,5) no funciona bien.