Análisis de la clasificación con curvas de características operativas del receptor
Los modelos de clasificación deben asignar un ejemplo a una categoría. Por ejemplo, debe usar características como el tamaño, el color y el movimiento para determinar si un objeto es un excursionista o un árbol.
Hay muchas maneras de mejorar los modelos de clasificación. Por ejemplo, podemos asegurarnos de que nuestros datos están equilibrados, limpios y escalados. También podemos modificar nuestra arquitectura de modelos y usar hiperparámetros para lograr el máximo rendimiento posible de nuestros datos y arquitectura. Finalmente, no encontramos ninguna manera mejor de mejorar el rendimiento en nuestro conjunto de pruebas (o datos de exclusión) y declarar que nuestro modelo está listo.
El ajuste del modelo en este punto puede ser complejo, pero podemos usar un sencillo paso final para mejorar aún más el buen funcionamiento de nuestro modelo. Sin embargo, para entender esto, es necesario volver a los aspectos básicos.
Probabilidades y categorías
Muchos modelos tienen varias fases de toma de decisiones y la última suele ser simplemente un paso de binarización. Durante la binarización, las probabilidades se convierten en una etiqueta dura. Por ejemplo, supongamos que el modelo se proporciona con características y calcula que existe una probabilidad del 75 % de que se mostrara un excursionista y del 25 % de que se mostrara un árbol. Un objeto no puede ser un 75 % excursionista y 25 % árbol; es una cosa o la otra. Como tal, el modelo aplica un umbral, que normalmente es del 50 %. Como la clase correspondiente al excursionista es mayor que el 50 %, se declara que el objeto es un excursionista.
El umbral del 50 % es lógico; significa que siempre se elige la etiqueta más probable según el modelo. Sin embargo, si el modelo está sesgado, es posible que este umbral del 50 % no sea adecuado. Por ejemplo, si el modelo tiene una ligera tendencia a elegir árboles, en lugar de excursionistas (la frecuencia con la que elige árboles es un 10 % mayor que la normal), podríamos ajustar nuestro umbral de decisión para tenerlo en cuenta.
Actualizador en función de las matrices de decisión
Las matrices de decisión son una excelente manera de evaluar los tipos de errores que está cometiendo un modelo. Esto nos proporciona las tasas de verdaderos positivos (VP), verdaderos negativos (VN), falsos positivos (FP) y falsos negativos (FN)

Podemos calcular algunas características útiles a partir de la matriz de confusión. A continuación se muestran dos características populares:
- Tasa de verdaderos positivos (sensibilidad): la frecuencia con la que las etiquetas "True" se identifican correctamente como "True". Por ejemplo, la frecuencia con la que el modelo predice "excursionista" cuando lo que se muestra es un excursionista.
- Tasa de falsos positivos (índice de falsas alarmas): la frecuencia con la que las etiquetas "False" se identifican incorrectamente como "True". Por ejemplo, la frecuencia con la que el modelo predice "excursionista" cuando se muestra un árbol.
El examen de las tasas de verdaderos positivos y falsos positivos puede ayudarnos a comprender el rendimiento de un modelo.
Considere nuestro ejemplo del excursionista. Lo ideal sería que la tasa de verdaderos positivos fuera muy alta, mientras que la de los falsos positivos fuera muy baja, ya que esto significaría que el modelo identifica bien a los excursionistas y no identifica a árboles como excursionistas con mucha frecuencia. Sin embargo, si la tasa de verdaderos positivos es muy alta, pero la de falsos positivos también lo es, el modelo está sesgado, es decir, identifica casi todo lo que encuentra como excursionista. Tampoco es deseable un modelo con una tasa de verdaderos positivos baja, ya que, cuando el modelo encuentre un excursionista, lo etiquetará como un árbol.
Curvas ROC
Las curvas de características operativas del receptor (ROC) son un gráfico en el que se traza la tasa de verdaderos positivos frente a la tasa de falsos positivos.
Las curvas de ROC pueden resultar confusas para principiantes por dos motivos principales. El primer motivo es que los principiantes saben que un modelo solo tiene un valor para las tasas de verdaderos positivos y verdaderos negativos, por lo que los trazados de ROC deben ser como este:
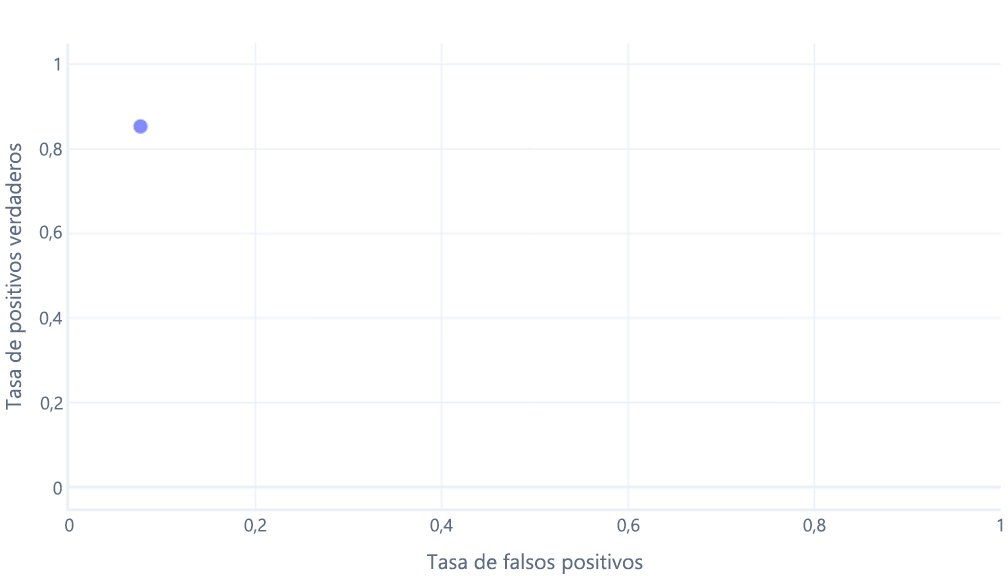
Si también piensa esto, está en lo cierto. Un modelo entrenado solo genera un punto. Sin embargo, recuerde que nuestros modelos tienen un umbral (normalmente el 50 %) que se usa para decidir si se debe utilizar la etiqueta true (excursionista) o false (árbol). Si cambiamos este umbral al 30 % y recalculamos las tasas de verdaderos positivos y falsos positivos, obtenemos otro punto:
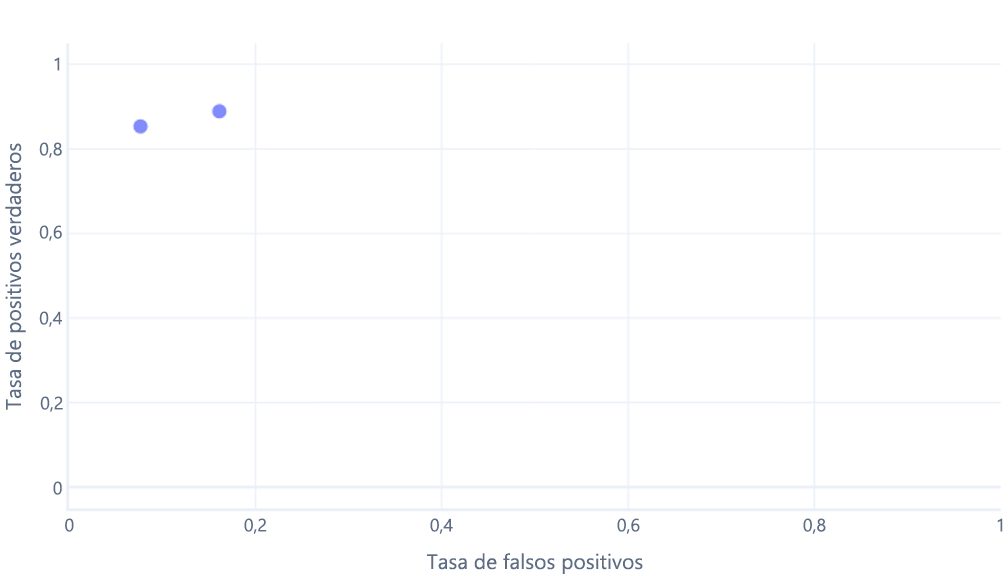
Si lo hacemos para umbrales entre el 0 % y el 100 %, podríamos obtener un grafo como el siguiente:
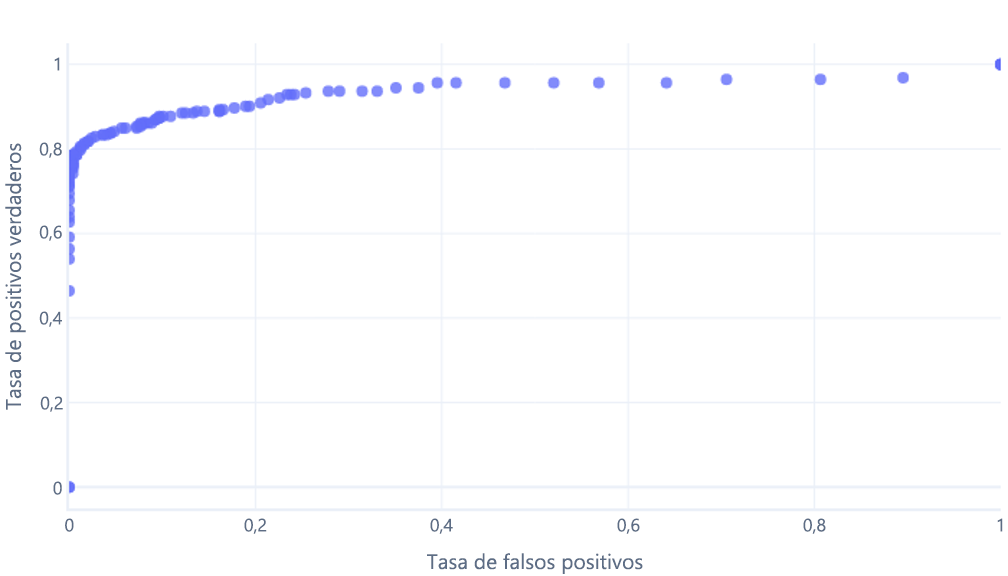
que normalmente mostramos como una línea, en su lugar:
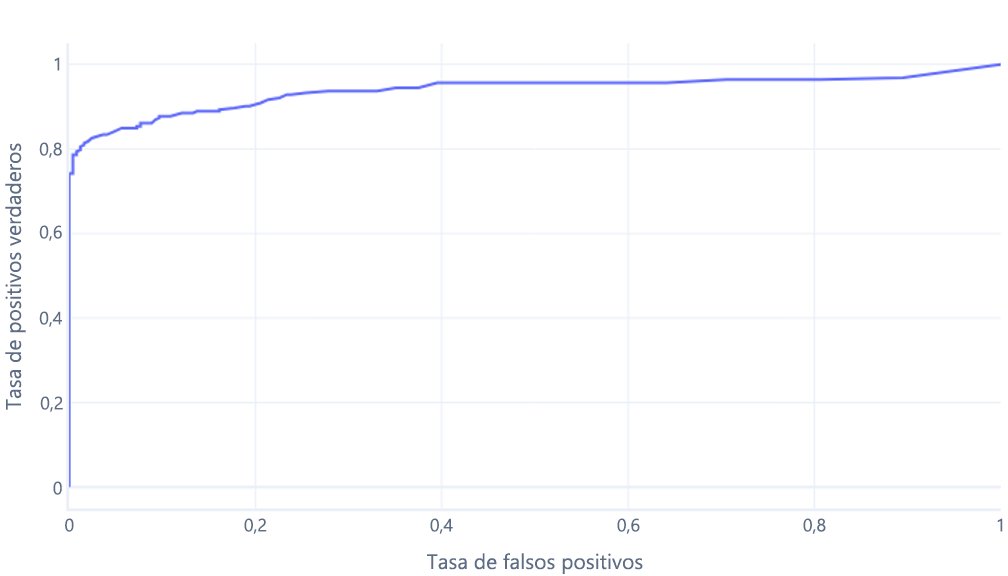
El segundo motivo por el que estos gráficos pueden resultar confusos es la jerga implicada. Recuerde que queremos una tasa de verdaderos positivos alta (que identifique a los excursionistas como tales) y una tasa de falsos positivos baja (que no identifique los árboles como excursionistas).
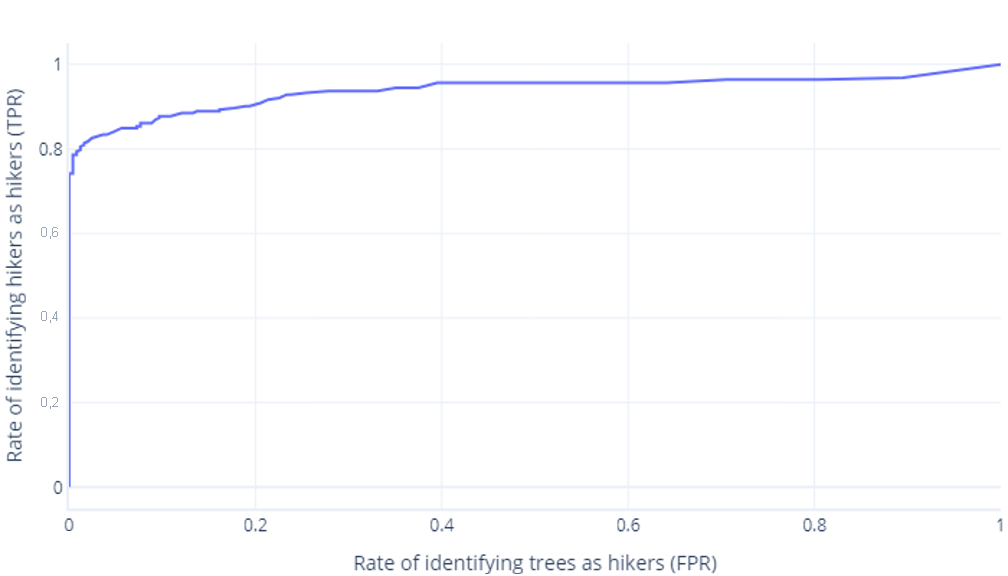
ROC buenas, ROC malas
Comprender las curvas de ROC buenas y malas es algo que se hace mejor en un entorno interactivo. Cuando esté listo, vaya al ejercicio siguiente para explorar este tema.