Árboles de decisión y arquitectura de modelos
Cuando se habla de arquitectura, a menudo pensamos en edificios. La arquitectura es responsable de la estructura de un edificio: su altura, profundidad, número de plantas y cómo se conectan las cosas internamente. Esta arquitectura también determina cómo usamos un edificio: por dónde entramos y qué podemos "obtener de él", en términos prácticos.
En el aprendizaje automático, la arquitectura hace referencia a un concepto similar. ¿Cuántos parámetros tiene y cómo están vinculados para lograr un cálculo? ¿Realizamos muchos cálculos en paralelo (ancho) o tenemos operaciones en serie que se basan en un cálculo anterior (profundidad)? ¿Cómo se pueden proporcionar entradas a este modelo y cómo se pueden recibir salidas? Estas decisiones de arquitectura solo se aplican normalmente a modelos más complejos y pueden variar desde las más sencillas a las más complejas. Estas decisiones se suelen tomar antes de entrenar el modelo, aunque, en algunas circunstancias, hay margen para realizar cambios después del entrenamiento.
Vamos a explorar este escenario usando concretamente árboles de decisión como ejemplo.
¿Qué es un árbol de decisión?
Básicamente, un árbol de decisión es un diagrama de flujo. Los árboles de decisión son un modelo de categorización que divide las decisiones en varios pasos.
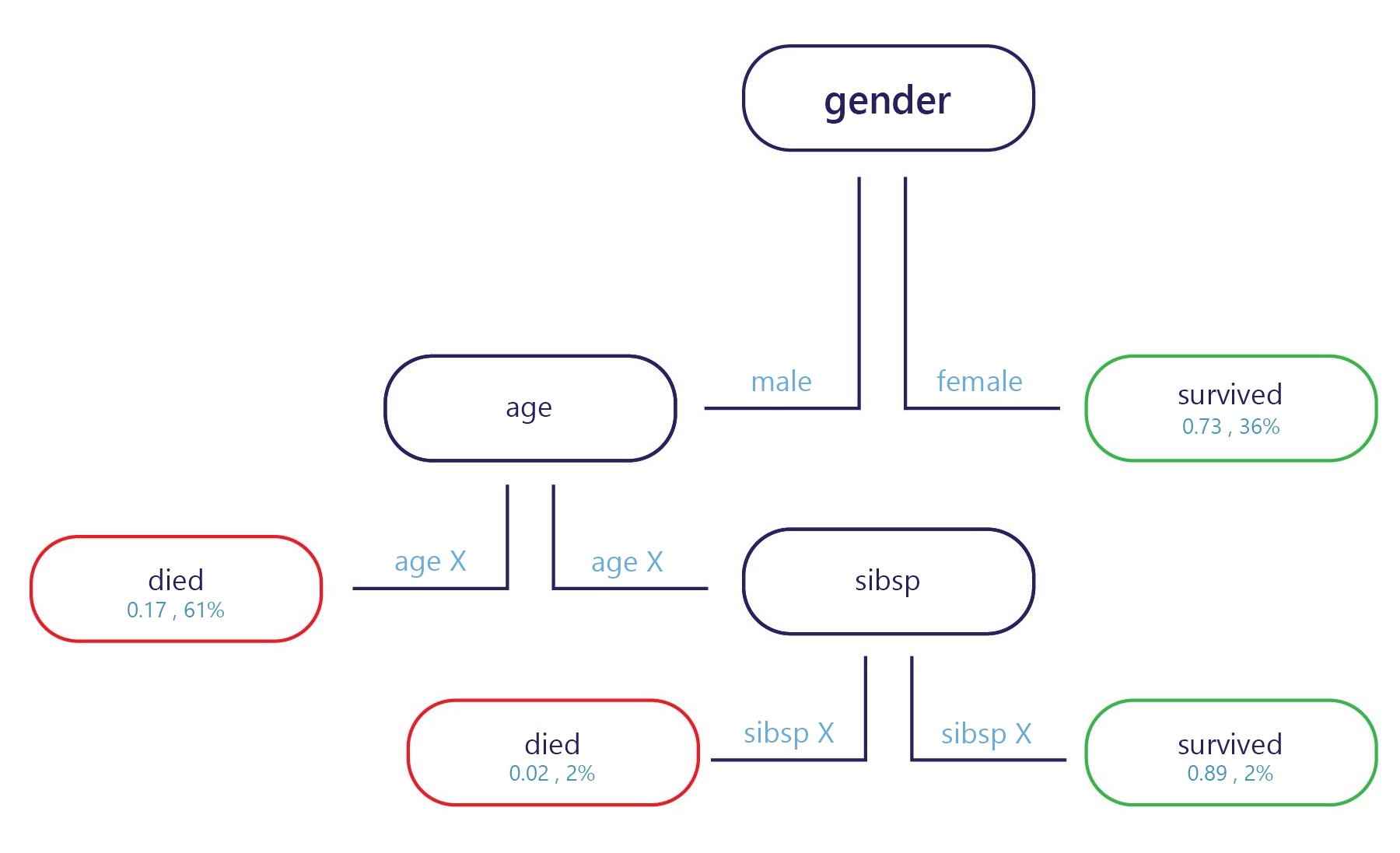
La muestra se proporciona en el punto de entrada (arriba, en el diagrama anterior) y cada punto de salida tiene una etiqueta (abajo en el diagrama). En cada nodo, una instrucción simple "if" decide a qué rama pasa la muestra a continuación. Una vez que la rama ha llegado al final del árbol (las hojas), se le asigna una etiqueta.
¿Cómo se entrenan los árboles de decisión?
En los árboles de decisión se entrena un nodo o punto de decisión cada vez. En el primer nodo, se evalúa todo el conjunto de entrenamiento. A partir de ahí, se selecciona una característica que pueda separar mejor el conjunto en dos subconjuntos que tengan etiquetas más homogéneas. Por ejemplo, imagine que nuestro conjunto de entrenamiento fuera el siguiente:
| Peso (característica) | Edad (característica) | Ganó una medalla (etiqueta) |
|---|---|---|
| 90 | 18 | No |
| 80 | 20 | No |
| 70 | 19 | No |
| 70 | 25 | No |
| 60 | 18 | Sí |
| 80 | 28 | Sí |
| 85 | 26 | Sí |
| 90 | 25 | Sí |
Si estamos haciendo todo lo posible para encontrar una regla que divida estos datos, podríamos hacerlo por edad, en torno a 24 años, porque la mayoría de los medallistas tenían más de 24 años. Esta división nos proporcionaría dos subconjuntos de datos.
Subconjunto 1
| Peso (característica) | Edad (característica) | Ganó una medalla (etiqueta) |
|---|---|---|
| 90 | 18 | No |
| 80 | 20 | No |
| 70 | 19 | No |
| 60 | 18 | Sí |
Subconjunto 2
| Peso (característica) | Edad (característica) | Ganó una medalla (etiqueta) |
|---|---|---|
| 70 | 25 | No |
| 80 | 28 | Sí |
| 85 | 26 | Sí |
| 90 | 25 | Sí |
Si nos detenemos aquí, tenemos un modelo sencillo con un nodo y dos hojas. La hoja 1 contiene los que no ganaron medalla y tiene una precisión del 75 % en nuestro conjunto de entrenamiento. La hoja 2 contiene los medallistas y también tiene una precisión del 75 % en el conjunto de entrenamiento.
Sin embargo, no es necesario detenerse aquí. Podemos continuar este proceso y seguir dividiendo las hojas.
En el subconjunto 1, el primer nodo nuevo podría dividirse por el peso, ya que el único medallista tenía un peso inferior a los que no ganaron una medalla. La regla puede establecerse en "peso < 65". Se predice que las personas con un peso < 65 ganarán una medalla, aunque las personas con un peso ≥ 65 no cumplen este criterio, y es posible que no ganen una medalla.
En el subconjunto 2, el segundo nodo nuevo también podría dividirse por el peso, pero esta vez se predice que cualquier persona con un peso superior a 70 habría ganado una medalla, mientras que los que están por debajo de ese peso no.
Esto nos proporcionaría un árbol que podría lograr una precisión del 100 % en el conjunto de entrenamiento.
Puntos fuertes y débiles de los árboles de decisión
Se considera que los árboles de decisión tienen un sesgo bajo. Esto significa que suelen ser buenos para identificar características que son importantes para etiquetar algo correctamente.
La principal debilidad de los árboles de decisión es el sobreajuste. Tenga en cuenta el ejemplo anterior: el modelo proporciona una manera exacta de calcular quién es probable que gane una medalla, de forma que se predecirá correctamente el 100 % del conjunto de datos de entrenamiento. Este nivel de precisión es inusual para los modelos de aprendizaje automático, que normalmente producen numerosos errores en el conjunto de datos de entrenamiento. Un buen rendimiento del entrenamiento no es algo malo en sí mismo, pero el árbol se ha especializado tanto en el conjunto de entrenamiento que es probable que no le vaya bien en el conjunto de pruebas. El motivo es que el árbol ha logrado aprender relaciones en el conjunto de entrenamiento que probablemente no son reales, como que tener un peso de 60 kilos garantiza una medalla si se tienen menos de 25 años.
La arquitectura del modelo afecta al sobreajuste
La forma en que estructuramos el árbol de decisión es clave para evitar sus puntos débiles. Cuanto más profundo sea el árbol, más probable es que se sobreajuste el conjunto de entrenamiento. Por ejemplo, en el árbol simple anterior, si limitásemos el árbol a solo el primer nodo, se producirían errores en el conjunto de entrenamiento, pero es probable que funcionara mejor en el conjunto de pruebas. El motivo es que habría reglas más generales sobre quién gana una medalla, por ejemplo, "atletas mayores de 24 años", en lugar de reglas muy específicas que solo se podrían aplicar al conjunto de entrenamiento.
Aunque aquí nos centramos en los árboles, otros modelos complejos suelen tener puntos débiles similares que se pueden mitigar a través de decisiones sobre cómo se estructuran o cómo pueden manipularse en el entrenamiento.