Vectores one-hot
Hasta ahora, hemos abordado la codificación de datos continuos (números de punto flotante), datos ordinales (normalmente enteros) y datos categóricos binarios (supervivientes/fallecidos, hombres/mujeres, etc.).
Ahora aprenderemos a codificar datos y veremos recursos de datos categóricos que tienen más de dos clases. También veremos los efectos potencialmente perjudiciales de nuestras decisiones de mejora del modelo sobre su rendimiento.
Los datos categóricos no son numéricos
Los datos categóricos no funcionan con números del mismo modo que otros tipos de datos funcionan con números. Con los datos ordinales o continuos (numéricos), los valores más altos implican un aumento de la cantidad. Por ejemplo, un precio de billete de 30 £ del Titanic es más caro que el de un billete de 12 £.
Por el contrario, los datos categóricos no tienen ningún orden lógico. Tendremos problemas si intentamos codificar como números características categóricas que tengan más de dos clases.
Por ejemplo, la opción del Puerto de embarque tiene tres valores: C (Cherburgo), Q (Queenstown) y S (Southampton). No podemos reemplazar estos símbolos por números. Si lo hacemos, implicará que uno de estos puertos es menor que los otros puertos, mientras que otro es mayor que los demás puertos. Este reemplazo no tiene sentido.
Como ejemplo de este problema, pasaremos a otra cosa y modelaremos la relación entre el Puerto de embarque y la Clase de billete, tratando el Puerto de embarque como un número. En primer lugar, se establece C < S < Q:
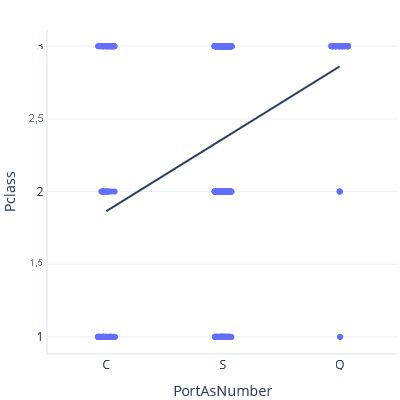
En el trazado anterior, la línea predice una clase de ~3 para el puerto Q.
Sin embargo, si establecemos S < C < Q, obtenemos una línea de tendencia y una predicción diferentes:
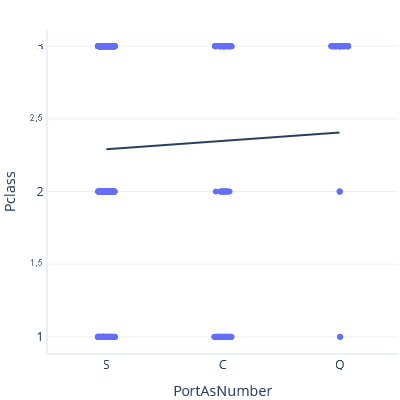
Ninguna de estas líneas de tendencia es correcta. No tiene sentido tratar las categorías como características continuas. ¿Cómo se trabaja entonces con categorías?
Codificación one-hot
La codificación one-hot puede codificar datos categóricos de una forma que evita este problema. Cada categoría disponible obtiene su propia columna y una fila determinada contiene un único valor 1 en la categoría a la que pertenece.
Por ejemplo, podemos codificar el valor del puerto en tres columnas, una para Cherbourg, otra para Queenstown y otra para Southampton (el orden exacto aquí no tiene relevancia). Una persona que embarcara en Cherbourg tendría un 1 en la columna Port_Cherbourg, de esta forma:
| Port_Cherbourg | Port_Queenstown | Port_Southampton |
|---|---|---|
| 1 | 0 | 0 |
Una persona que embarcara en Queenstown tendría un 1 en la segunda columna:
| Port_Cherbourg | Port_Queenstown | Port_Southampton |
|---|---|---|
| 0 | 1 | 0 |
Una persona que embarcara en Southampton tendría un 1 en la tercera columna:
| Port_Cherbourg | Port_Queenstown | Port_Southampton |
|---|---|---|
| 0 | 0 | 1 |
Codificación one-hot, limpieza de datos y potencia estadística
Antes de usar la codificación one-hot, es importante comprender que su uso puede tener un impacto positivo o negativo en el rendimiento real de un modelo.
¿Qué es la potencia estadística?
Eficacia estadística hace referencia a la capacidad de un modelo para identificar de forma confiable las relaciones reales entre las características y las etiquetas. Por ejemplo, un modelo eficaz podría informar de la relación entre el precio del billete y la tasa de supervivencia con un alto grado de certeza. Por el contrario, un modelo con poca eficacia estadística podría informar de una relación con un bajo grado de certeza, o incluso podría no encontrar la relación en absoluto.
Aquí evitaremos las matemáticas, pero recuerde que las decisiones que tomamos pueden influir en la eficacia de los modelos.
La eliminación de datos reduce la potencia estadística
Hemos mencionado varias veces que la limpieza de datos (en parte) implica la eliminación de muestras de datos incompletas. Lamentablemente, la limpieza de datos puede reducir la eficacia estadística. Por ejemplo, supongamos que queremos predecir la supervivencia de la travesía del Titanic con los siguientes datos:
| Precio del billete | Supervivencia |
|---|---|
| 4 £ | 0 |
| 8 £ | 0 |
| 10 £ | 1 |
| 25 £ | 1 |
Podríamos suponer que los pasajeros con un billete de 15 £ sobrevivieron, porque todas las personas con billetes de 10 £ o más sobrevivieron. Sin embargo, si tuviéramos menos datos, esta suposición sería más difícil:
| Precio del billete | Supervivencia |
|---|---|
| 4 £ | 0 |
| 8 £ | 0 |
| 25 £ | 1 |
Las columnas sin valor reducen la potencia estadística
Las características que tienen poco valor también pueden dañar la eficacia estadística, especialmente cuando el número de características (o columnas) comienza a aproximarse al número de muestras (o filas).
Por ejemplo, supongamos que queremos predecir la supervivencia con los siguientes datos:
| Precio del billete | Supervivencia |
|---|---|
| 4 £ | 0 |
| 4 £ | 0 |
| 25 £ | 1 |
| 25 £ | 1 |
Podríamos predecir con seguridad que quienes tenían un billete para un camarote A sobrevivieron, porque todos los que tenían billetes de 25 £ sobrevivieron.
Sin embargo, ahora tenemos otra característica (camarote):
| Precio del billete | Cabin | Supervivencia |
|---|---|---|
| 4 £ | A | 0 |
| 4 £ | A | 0 |
| 25 £ | B | 1 |
| 25 £ | B | 1 |
La columna Cabina no proporciona información útil, ya que simplemente corresponde al precio del billete. No está claro si alguien con un billete de 25 £ Camarote A sobreviviría. ¿Muere, como otros de Camarote A, o sobrevive como aquellos con billetes de 25 £?
La codificación one-hot puede reducir la potencia estadística
La codificación one-hot reduce la eficacia estadística mucho más que los datos continuos u ordinales, porque requiere varias columnas, una para cada valor categórico posible. Por ejemplo, si codificamos un solo acceso al puerto de embarque, agregamos tres entradas de modelo (C, S y Q).
Una variable categórica resulta útil si el número de categorías es considerablemente inferior al número de muestras (filas del conjunto de datos). Una variable categórica también resulta útil si proporciona información que aún no está disponible para el modelo a través de otras entradas.
Por ejemplo, vimos que la probabilidad de supervivencia era distinta para las personas que embarcaron en puertos diferentes. Probablemente, esta variación refleja el hecho de que la mayoría de las personas del puerto Queenstown tenían billetes de tercera clase. Por tanto, el embarque probablemente reduce la eficacia estadística en cierto grado, sin agregar información relevante a nuestro modelo.
Por el contrario, Camarote probablemente tiene una fuerte influencia en la supervivencia. Esto se debe a que los camarote inferiores del barco se habrían llenado de agua antes de que loas camarote más cercanas a la cubierta superior del barco. Dicho esto, el conjunto de datos del Titanic contiene 147 camarotes diferentes. Esto reduce la eficacia estadística de nuestro modelo si los incluimos. Es posible que tengamos que experimentar con la inclusión o exclusión de datos de los camarotes en el modelo, para ver si son útiles o no.
En el siguiente ejercicio, crearemos finalmente nuestro modelo de predicción de la tasa de supervivencia del Titanic y practicaremos la codificación one-hot durante este proceso.