Optimización de modelos mediante el descenso de gradiente

  • 6 minutos

Hemos visto cómo las funciones de costo evalúan el rendimiento de los modelos mediante el uso de datos. El optimizador es la parte final del rompecabezas.

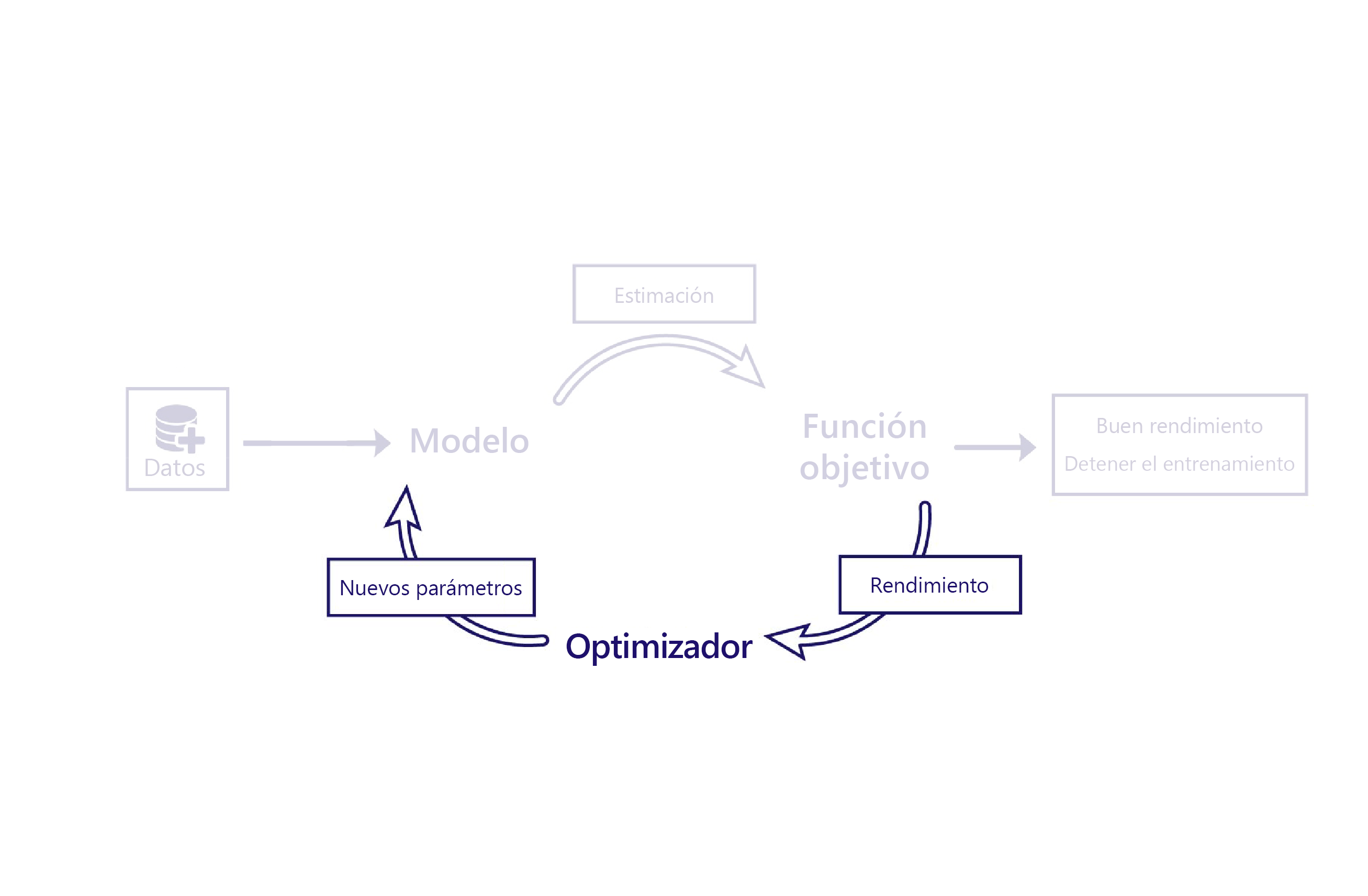
El rol del optimizador es modificar el modelo de forma que mejore su rendimiento. Para ello, altera las salidas y el costo del modelo y sugiere nuevos parámetros para dicho modelo.

Por ejemplo, en el escenario de la granja, el modelo lineal tiene dos parámetros: la intersección de la línea y la pendiente de la línea. Si la intersección de la línea es incorrecta, el modelo infravalora o sobrevalora las temperaturas de media. Si la pendiente se establece mal, el modelo no hace un buen trabajo para demostrar cómo han cambiado las temperaturas desde 1950. El optimizador cambia estos dos parámetros para que modelen las temperaturas a lo largo de los años de forma óptima.

Diagrama en el que se muestra la parte del optimizador del ciclo de vida del aprendizaje automático.

Descenso de gradiente

El algoritmo de optimización más común en la actualidad es el descenso de gradiente. Existen diversas variantes de este algoritmo, pero todas usan los mismos conceptos básicos.

El descenso de gradiente calcula cómo los cambios realizados en cada parámetro modifican el coste mediante el uso del cálculo. Por ejemplo, se podría predecir que el aumento de un parámetro reducirá el costo.

El descenso de gradiente se denomina como tal porque calcula la gradiente (pendiente) de la relación entre cada parámetro del modelo y el costo. A continuación, se modifican los parámetros para bajar esta pendiente.

Este algoritmo es sencillo pero eficaz. Sin embargo, no garantiza encontrar unos parámetros del modelo óptimos que minimicen el costo. Las dos principales fuentes de error son los mínimos locales y la inestabilidad.

Mínimos locales

Nuestro ejemplo anterior parecía realizar un buen trabajo, suponiendo que el costo seguiría aumentando cuando el parámetro era menor que 0 o mayor que 10:

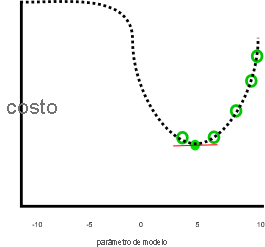
Trazado de la relación entre el costo y el parámetro del modelo, en el cual se muestra un costo que alcanza sus mínimos cuando el parámetro del modelo es cinco.

Este trabajo no parece ser tan grande si los parámetros menores que cero o mayores que 10 generaron costos más bajos, como en esta imagen:

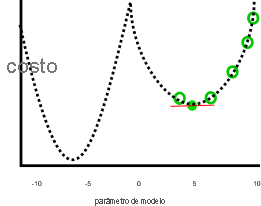
Trazado de la relación entre el costo y el parámetro del modelo, en el cual se muestra un costo que alcanza unos mínimos locales cuando el parámetro del modelo es 5, pero que es aún menor cuando el parámetro del modelo está en −6.

En el gráfico anterior, un valor de parámetro de siete negativos sería una solución mejor que cinco, ya que tiene un costo menor. El descenso de degradado no conoce la relación completa entre cada parámetro y el costo (representado por la línea) de puntos de antemano. Por lo tanto, es propenso a buscar los mínimos locales: estimaciones de parámetros que no son la mejor solución, pero cuyo gradiente es cero.

Inestabilidad

Un problema relacionado es que el descenso de gradiente a veces muestra inestabilidad. Esta inestabilidad suele producirse cuando el tamaño del paso o la velocidad de aprendizaje hacen (que cada parámetro se ajuste por cada iteración) es demasiado grande. En ese caso, los parámetros se ajustan demasiado lejos en cada paso y el modelo se vuelve, de hecho, menos eficaz con cada iteración:

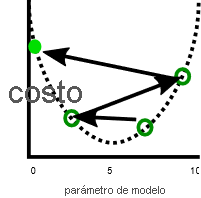
Gráfico de la relación entre el costo y el parámetro del modelo, en el cual se muestra un costo que se mueve con pasos grandes, con una reducción mínima del costo.

Una velocidad de aprendizaje más lenta puede resolver este problema, pero también puede plantear otros. En primer lugar, las velocidades de aprendizaje más lentas pueden hacer que el entrenamiento dure mucho tiempo, ya que se necesitan más pasos. En segundo lugar, realizar pasos más pequeños hace que sea más probable que el entrenamiento se resuelva en mínimos locales:

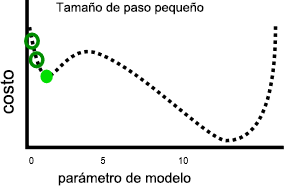
Gráfico de la relación entre el costo y el parámetro del modelo, que muestra movimientos pequeños en el costo.

Por el contrario, una velocidad de aprendizaje más rápida puede facilitar la tarea de evitar alcanzar los mínimos locales, ya que los pasos más grandes pueden saltarse los máximos locales:

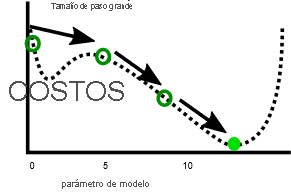
Gráfico de la relación entre el costo y el parámetro del modelo, que muestra los movimientos regulares del costo hasta que se alcanzan unos mínimos.

Como veremos en el ejercicio siguiente, hay un tamaño de paso óptimo para cada problema. Encontrar este punto óptimo es algo que a menudo requiere experimentación.