Aprendizaje profundo

Completado

El aprendizaje profundo es una forma avanzada de aprendizaje automático que intenta emular el modo en que el cerebro humano aprende. La clave del aprendizaje profundo es la creación de una red neuronal artificial que simula la actividad electroquímica de las neuronas biológicas mediante el uso de funciones matemáticas, como se muestra aquí.

Red neuronal biológica	Red neuronal artificial
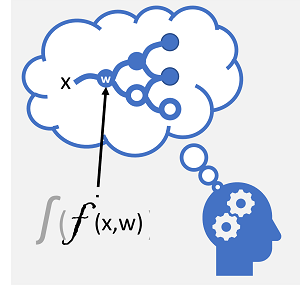
Las neuronas se activan en respuesta a estímulos electroquímicos. Cuando se activa, la señal se pasa a las neuronas conectadas.	Cada neurona es una función que funciona en un valor de entrada (x) y un peso (w). La función se ajusta en una función de activación que determina si se debe transmitir la salida.

Las redes neuronales artificiales se componen de varias capas de neuronas, básicamente definiendo una función profundamente anidada. Esta arquitectura es la razón por la que la técnica se denomina aprendizaje profundo y los modelos que producen suelen denominarse redes neuronales profundas (DNN). Puede usar redes neuronales profundas para muchos tipos de problemas de aprendizaje automático, incluida la regresión y la clasificación, así como modelos más especializados para el procesamiento de lenguaje natural y la visión artificial.

Al igual que otras técnicas de aprendizaje automático descritas en este módulo, el aprendizaje profundo implica ajustar los datos de entrenamiento a una función que puede predecir una etiqueta (y) en función del valor de una o varias características (x). La función (f(x)) es la capa externa de una función anidada en la que cada capa de la red neuronal encapsula funciones que operan sobre x y los valores de peso (w) asociados a ellas. El algoritmo utilizado para entrenar el modelo implica alimentar iterativamente los valores de las características (x) en los datos de entrenamiento a través de las capas para calcular los valores de salida para ŷ, validar el modelo para evaluar la distancia que separa los valores ŷ calculados de los valores y conocidos (lo que cuantifica el nivel de error, o pérdida, en el modelo), y luego modificar los pesos (w) para reducir la pérdida. El modelo entrenado incluye los valores de peso finales que dan como resultado las predicciones más precisas.

Ejemplo: uso del aprendizaje profundo para la clasificación

Para comprender mejor cómo funciona un modelo de red neuronal profunda, vamos a explorar un ejemplo en el que se usa una red neuronal para definir un modelo de clasificación para las especies pingüinos.

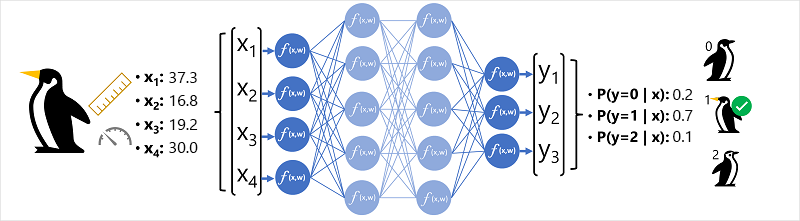
Los datos de características (x) consisten en algunas medidas de un pingüino. Específicamente, las medidas son las siguientes:

• El largo del pico del pingüino.
• La profundidad del pico del pingüino.
• El largo de las aletas del pingüino.
• El peso del pingüino.

En este caso, las características x es un vector de cuatro valores, o bien, matemáticamente expresado, x=[x1,x2,x3,x4].

La etiqueta que se intenta predecir (y) es la especie del pingüino y que hay tres posibilidades de especie:

• Adelia
• Papúa
• Barbijo

Este es un ejemplo de un problema de clasificación, en el que el modelo de Machine Learning debe predecir la clase más probable a la que pertenece una observación. Un modelo de clasificación logra esto mediante la predicción de una etiqueta que consta de la probabilidad de cada clase. En otras palabras, y es un vector de valores de tres probabilidades, una para cada una de las posibles clases: [P(y=0|x), P(y=1|x), P(y=2|x)].

El proceso para inferir una clase de pingüino predicha utilizando esta red es:

1. El vector de características de una observación de un pingüino se introduce en la capa de entrada de la red neuronal, que consta de una neurona para cada valor x. En este ejemplo, se usa el siguiente vector x como entrada: [37.3, 16.8, 19.2, 30.0]
2. Cada una de las funciones de la primera capa de neuronas calcula una suma ponderada combinando el valor x y el peso w, y la transmite a una función de activación que determina si cumple el umbral para pasar a la siguiente capa.
3. Cada neurona de una capa está conectada a todas las neuronas de la capa siguiente (una arquitectura a veces denominada red totalmente conectada), por lo que los resultados de cada capa se reenvían a través de la red hasta que llegan a la capa de salida.
4. La capa de salida genera un vector de valores; en este caso, con una función softmax o similar para calcular la distribución de probabilidad para las tres clases posibles de pingüino. En este ejemplo, el vector de salida es: [0,2, 0,7, 0,1]
5. Los elementos del vector representan las probabilidades de las clases 0, 1 y 2. El segundo valor es el más alto, por lo que el modelo predice que la especie del pingüino es 1 (Gentoo).

¿Cómo aprende una red neuronal?

Los pesos de una red neuronal son fundamentales para calcular los valores previstos de las etiquetas. Durante el proceso de entrenamiento, el modelo aprende los pesos que darán lugar a las predicciones más precisas. Vamos a explorar el proceso de entrenamiento con un poco más de detalle para comprender cómo tiene lugar este aprendizaje.

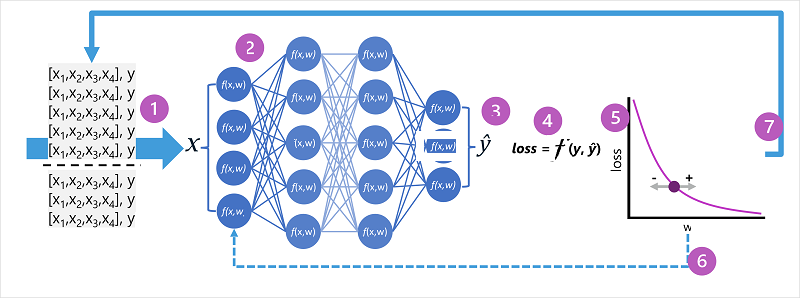
1. Se definen los conjuntos de datos de entrenamiento y validación, y las características de entrenamiento se introducen en la capa de entrada.
2. Las neuronas de cada capa de la red aplican sus pesos (que inicialmente se asignan aleatoriamente) y alimentan los datos a través de la red.
3. La capa de salida genera un vector que contiene los valores calculados para ŷ. Por ejemplo, una salida para una predicción de la clase de pingüino podría ser [0.3. 0.1. 0.6].
4. Se usa una función de pérdida para comparar los valores previstos de ŷ con los valores yconocidos y agregar la diferencia (que se conoce como pérdida). Por ejemplo, si la clase conocida para el caso que devolvió la salida en el paso anterior es Chinstrap, el valor y debe ser [0,0, 0,0, 1,0]. La diferencia absoluta entre este y el vector ŷ es [0,3, 0,1, 0,4]. En realidad, la función de pérdida calcula la varianza agregada para varios casos y la resume como un único valor de pérdida.
5. Dado que toda la red es esencialmente una gran función anidada, una función de optimización puede utilizar el cálculo diferencial para evaluar la influencia de cada peso de la red en la pérdida, y determinar cómo podrían ajustarse (hacia arriba o hacia abajo) para reducir la cantidad de pérdida global. La técnica de optimización específica puede variar, pero normalmente implica un enfoque de descenso de gradiente en el que cada peso aumenta o disminuye para minimizar la pérdida.
6. Los cambios en los pesos se vuelven a aplicar a las capas de la red, reemplazando los valores usados anteriormente.
7. El proceso se repite en varias iteraciones (conocidas como épocas) hasta que se minimiza la pérdida y el modelo predice con una precisión aceptable.

Nota:

Aunque es más fácil pensar que cada caso de los datos de entrenamiento pasa por la red de uno en uno, en realidad los datos se procesan por lotes en matrices y se procesan mediante cálculos algebraicos lineales. Por este motivo, el entrenamiento de red neuronal se realiza mejor en equipos con unidades de procesamiento gráfico (GPU) optimizadas para la manipulación de vectores y matrices.