Clasificación multiclase
La clasificación multiclase se usa para predecir a qué clases posibles pertenece una observación. Como técnica de aprendizaje automático supervisado, sigue el mismo proceso iterativo de entrenamiento, validación y evaluación que la regresión y la clasificación binaria, en el que se mantiene un subconjunto de los datos de entrenamiento para validar el modelo entrenado.
Ejemplo: clasificación multiclase
Los algoritmos de clasificación multiclase se usan para calcular valores de probabilidad para varias etiquetas de clase, lo que permite a un modelo predecir la clase más probable para una observación determinada.
Ahora se verá un ejemplo con varias observaciones de pingüinos, en el que se registra la longitud de las alas (x) de cada pingüino. Para cada observación, los datos incluyen la especie del pingüino (y), que se codifica de la siguiente manera:
- 0: Adelia
- 1: Papúa
- 2: Barbijo
Nota:
Como en los ejemplos anteriores de este módulo, en un escenario real se incluirían varios valores de característica (x). Aquí se usará una sola característica para simplificar las cosas.
 |
 |
|---|---|
| Longitud de las alas (x) | Especie (y) |
| 167 | 0 |
| 172 | 0 |
| 225 | 2 |
| 197 | 1 |
| 189 | 1 |
| 232 | 2 |
| 158 | 0 |
Entrenamiento de un modelo de clasificación multiclase
Para entrenar un modelo de clasificación multiclase, es necesario usar un algoritmo para ajustar los datos de entrenamiento a una función que calcule un valor de probabilidad para cada clase posible. Para ello puede usar dos tipos de algoritmo:
- Algoritmos Uno frente a todos (OvR)
- Algoritmos multinomiales
Algoritmos Uno frente a todos (OvR)
Los algoritmos de tipo Uno frente a todos entrenan una función de clasificación binaria para cada clase, y en cada una se calcula la probabilidad de que la observación sea un ejemplo de la clase de destino. Cada función calcula la probabilidad de que la observación sea una clase específica en comparación con cualquier otra clase. Para el modelo de clasificación de especies de pingüinos, el algoritmo básicamente crearía tres funciones de clasificación binaria:
- f0(x) = P(y=0 | x)
- f1(x) = P(y=1 | x)
- f2(x) = P(y=2 | x)
Cada algoritmo genera una función sigmoide que calcula un valor de probabilidad entre 0,0 y 1,0. Un modelo entrenado con este tipo de algoritmo predice la clase para la función que genera la salida de probabilidad más alta.
Algoritmos multinomiales
Como enfoque alternativo, se puede usar un algoritmo multinomial, que crea una única función que devuelve una salida multivalor. La salida es un vector (una matriz de valores) que contiene la distribución de probabilidad para todas las clases posibles, con una puntuación de probabilidad para cada clase que, cuando se totaliza, suma hasta 1,0:
f(x) =[P(y=0|x), P(y=1|x), P(y=2|x)]
Un ejemplo de este tipo de función es softmax, que podría generar una salida como la del ejemplo siguiente:
[0.2, 0.3, 0.5]
Los elementos del vector representan las probabilidades de las clases 0, 1 y 2 respectivamente; por tanto, en este caso, la clase con la probabilidad más alta es 2.
Independientemente del tipo de algoritmo que se use, el modelo utiliza la función resultante para determinar la clase más probable para un conjunto determinado de características (x) y predice la etiqueta de clase correspondiente (y).
Evaluación de un modelo de clasificación multiclase
Puede evaluar un clasificador multiclase si calcula las métricas de clasificación binaria para cada clase individual. Como alternativa, puede calcular las métricas agregadas que tienen en cuenta todas las clases.
Imagine que ha validado el clasificador multiclase y ha obtenido los siguientes resultados:
| Longitud de las alas (x) | Especies reales (y) | Especies predichas (ŷ) |
|---|---|---|
| 165 | 0 | 0 |
| 171 | 0 | 0 |
| 205 | 2 | 1 |
| 195 | 1 | 1 |
| 183 | 1 | 1 |
| 221 | 2 | 2 |
| 214 | 2 | 2 |
La matriz de confusión de un clasificador multiclase es similar a la de un clasificador binario, salvo que muestra el número de predicciones para cada combinación de las etiquetas de clase predicha (ŷ) y real (y):
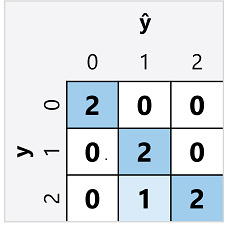
A partir de esta matriz de confusión, se pueden determinar las métricas de cada clase individual de la siguiente manera:
| Clase | TP | TN | FP | FN | Exactitud | Recuperación | Precisión | Puntuación F1 |
|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 5 | 0 | 0 | 1,0 | 1,0 | 1,0 | 1,0 |
| 1 | 2 | 4 | 1 | 0 | 0,86 | 1.0 | 0,67 | 0.8 |
| 2 | 2 | 4 | 0 | 1 | 0,86 | 0,67 | 1.0 | 0.8 |
Para calcular las métricas de exactitud y coincidencia generales, use el total de las métricas TP, TN, FP t FN:
- Exactitud general = (13+6)÷(13+6+1+1) = 0,90
- Coincidencia general = 6÷(6+1) = 0,86
- Precisión general = 6÷(6+1) = 0,86
La puntuación general F1 se calcula con las métricas de precisión y coincidencia generales:
- Puntuación general F1 = (2x0,86x0,86)÷(0,86+0,86) = 0,86