Clasificación binaria
La clasificación, como la regresión, es una técnica de aprendizaje automático supervisado y, por tanto, sigue el mismo proceso iterativo de entrenamiento, validación y evaluación de modelos. En lugar de calcular valores numéricos como un modelo de regresión, los algoritmos usados para entrenar modelos de clasificación calculan valores de probabilidad para la asignación de clases y las métricas de evaluación usadas para evaluar el rendimiento del modelo comparan las clases predichas con las clases reales.
Los algoritmos de clasificación binaria se usan para entrenar un modelo que predice una de las dos etiquetas posibles para una sola clase. Esencialmente, predecir verdadero o falso. En la mayoría de los escenarios reales, las observaciones de datos usadas para entrenar y validar el modelo consisten en valores de características múltiples (x) y un valor y que es 1 o 0.
Ejemplo: clasificación binaria
Para comprender cómo funciona la clasificación binaria, echemos un vistazo a un ejemplo simplificado que usa una sola característica (x) para predecir si la etiqueta y es 1 o 0. En este ejemplo, usaremos el nivel de glucosa en sangre de un paciente para predecir si el paciente tiene diabetes o no. Estos son los datos con los que entrenaremos el modelo:
 |
 |
|---|---|
| Glucosa en sangre (x) | ¿Diabético? (y) |
| 67 | 0 |
| 103 | 1 |
| 114 | 1 |
| 72 | 0 |
| 116 | 1 |
| 65 | 0 |
Entrenamiento de un modelo de clasificación binaria
Para entrenar el modelo, usaremos un algoritmo para ajustar los datos de entrenamiento a una función que calcula la probabilidad de que la etiqueta de clase sea verdadera (en otras palabras, que el paciente tenga diabetes). La probabilidad se mide como un valor entre 0,0 y 1,0, de modo que la probabilidad total de todas las clases posibles es 1,0. Así, por ejemplo, si la probabilidad de que un paciente tenga diabetes es de 0,7, existe una probabilidad correspondiente de 0,3 de que el paciente no sea diabético.
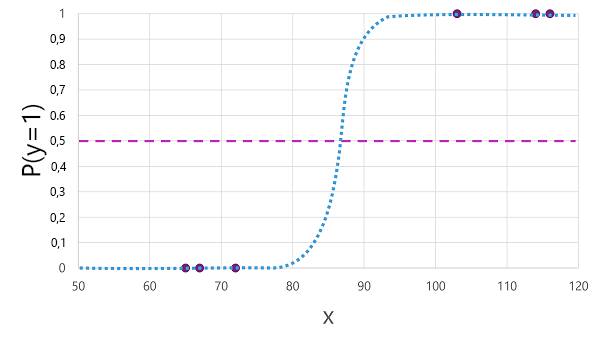
Hay muchos algoritmos que se pueden usar para la clasificación binaria, como la regresión logística, que deriva una sigmoide (en forma de S) con valores entre 0,0 y 1,0, de esta manera:
Nota:
A pesar de su nombre, en el aprendizaje automático la regresión logística se usa para la clasificación, no para la regresión. El punto importante es la naturaleza logística de la función que genera, que describe una curva en forma S entre un valor inferior y superior (0,0 y 1,0 cuando se usa para la clasificación binaria).
La función producida por el algoritmo describe la probabilidad de que y sea verdadero (y=1) para un valor dado de x. Matemáticamente, puede expresar la función de la siguiente manera:
f(x) = P(y=1 | x)
Para tres de las seis observaciones de los datos de entrenamiento, sabemos que y es definitivamente verdadero, por lo que la probabilidad para esas observaciones de que y=1 es 1,0 y para las otras tres, sabemos que y es definitivamente falso, por lo que la probabilidad de que y=1 es 0,0. La curva en forma de S describe la distribución de probabilidad, de modo que al trazar un valor de x sobre la línea se identifica la probabilidad correspondiente de que y sea 1.
El diagrama también incluye una línea horizontal para indicar el umbral en el que un modelo basado en esta función predecirá verdadero (1) o falso (0). El umbral se encuentra en el punto medio de y (P(y) = 0,5). Para cualquier valor en este punto o por encima, el modelo predecirá verdadero (1); mientras que para cualquier valor por debajo de este punto predecirá falso (0). Por ejemplo, para un paciente con un nivel de glucosa en sangre de 90, la función daría como resultado un valor de probabilidad de 0,9. Dado que 0,9 es mayor que el umbral de 0,5, el modelo predeciría true (1): es decir, se predice que el paciente tiene diabetes.
Evaluación de un modelo de clasificación binaria
Al igual que con la regresión, al entrenar un modelo de clasificación binaria, se mantiene un subconjunto aleatorio de datos con el que validar el modelo entrenado. Supongamos que retenemos los siguientes datos para validar nuestro clasificador de diabetes:
| Glucosa en sangre (x) | ¿Diabético? (y) |
|---|---|
| 66 | 0 |
| 107 | 1 |
| 112 | 1 |
| 71 | 0 |
| 87 | 1 |
| 89 | 1 |
La aplicación de la función logística que derivamos anteriormente a los valores de x da como resultado el siguiente gráfico.
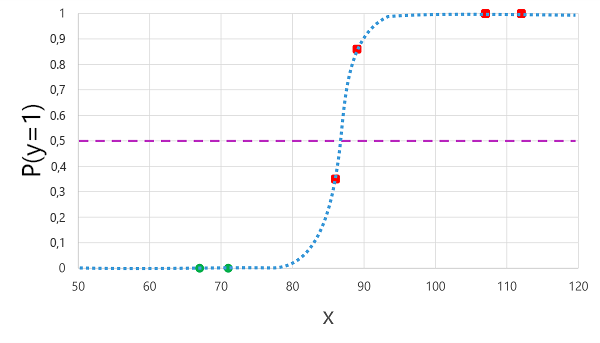
En función de si la probabilidad calculada por la función está por encima o por debajo del umbral, el modelo genera una etiqueta predicha de 1 o 0 para cada observación. A continuación, podemos comparar las etiquetas de clase predichas (ŷ) con las etiquetas de clase reales (y), como se muestra aquí:
| Glucosa en sangre (x) | Diagnóstico real de diabetes (y) | Diagnóstico de diabetes predicho (ŷ) |
|---|---|---|
| 66 | 0 | 0 |
| 107 | 1 | 1 |
| 112 | 1 | 1 |
| 71 | 0 | 0 |
| 87 | 1 | 0 |
| 89 | 1 | 1 |
Métricas de evaluación de clasificación binaria
El primer paso para calcular las métricas de evaluación para un modelo de clasificación binaria suele ser crear una matriz del número de predicciones correctas e incorrectas para cada etiqueta de clase posible:
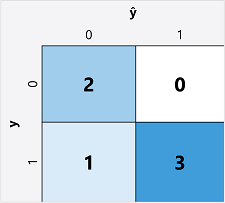
Esta visualización se denomina matriz de confusión y muestra los totales de predicción donde:
- ŷ=0 e y=0: Verdaderos negativos (TN por sus siglas en inglés)
- ŷ=1 e y=0: Falsos positivos (FP por sus siglas en inglés)
- ŷ=0 e y=1: Falsos negativos (FN por sus siglas en inglés)
- ŷ=1 e y=1: Verdaderos positivos (TP por sus siglas en inglés)
La disposición de la matriz de confusión es tal que las predicciones correctas (verdaderas) se muestran en una línea diagonal de la parte superior izquierda a la derecha. A menudo, la intensidad del color se usa para indicar el número de predicciones en cada celda, por lo que un vistazo rápido a un modelo que predice bien debe revelar una tendencia diagonal profundamente sombreada.
Precisión
La métrica más sencilla que se puede calcular a partir de la matriz de confusión es la precisión: la proporción de predicciones que el modelo acertó. La precisión se calcula como:
(TN+TP) ÷ (TN+FN+FP+TP)
En el caso de nuestro ejemplo de diabetes, el cálculo es:
(2+3) ÷ (2+1+0+3)
= 5 ÷ 6
= 0,83
Por lo tanto, para nuestros datos de validación, el modelo de clasificación de diabetes produjo predicciones correctas el 83 % del tiempo.
La precisión podría parecer inicialmente una buena métrica para evaluar un modelo, pero tenga en cuenta esto. Supongamos que el 11 % de la población tiene diabetes. Podría crear un modelo que siempre prediga 0 y lograría una precisión del 89 %, aunque no intente diferenciar entre pacientes mediante la evaluación de sus características. Lo que realmente necesitamos es una comprensión más profunda de cómo funciona el modelo en la predicción de 1 para casos positivos y 0 para casos negativos.
Coincidencia
Coincidencia es una métrica que mide la proporción de casos positivos que el modelo identificó correctamente. En otras palabras, en comparación con el número de pacientes que tienen diabetes, ¿cuántos predijo el modelo que tenían diabetes?
La fórmula para la coincidencia es:
TP ÷ (TP+FN)
Para nuestro ejemplo de diabetes:
3 ÷ (3+1)
= 3 ÷ 4
= 0,75
Así pues, nuestro modelo identificó correctamente como diabéticos al 75 % de los pacientes.
Precisión
Precisión es una métrica similar a la coincidencia, pero mide la proporción de casos positivos predichos en los que la etiqueta verdadera es realmente positiva. En otras palabras, ¿qué proporción de los pacientes predichos por el modelo como diabéticos tienen realmente diabetes?
La fórmula de precisión es:
TP ÷ (TP+FP)
Para nuestro ejemplo de diabetes:
3 ÷ (3+0)
= 3 ÷ 3
= 1,0
Así pues, el 100 % de los pacientes que nuestro modelo predijo que tienen diabetes, efectivamente la tienen.
Puntuación F1
Puntuación F1 es una métrica global que combina coincidencia y precisión. La fórmula de la puntuación F1 es:
(2 x precisión x coincidencia) ÷ (precisión + coincidencia)
Para nuestro ejemplo de diabetes:
(2 x 1,0 x 0,75) ÷ (1,0 + 0,75)
= 1,5 ÷ 1,75
= 0,86
Área bajo la curva (AUC)
Otro nombre para la coincidencia es la tasa de verdaderos positivos (TPR), y existe una métrica equivalente llamada tasa de falsos positivos (FPR) que se calcula como FP÷(FP+TN). Ya sabemos que la TPR de nuestro modelo cuando usamos un umbral de 0,5 es de 0,75, y podemos usar la fórmula de la TPR para calcular un valor de 0÷2 = 0.
Por supuesto, si cambiáramos el umbral a partir del cual el modelo predice verdadero (1), afectaría al número de predicciones positivas y negativas; y, por tanto, cambiarían las métricas TPR y FPR. Estas métricas suelen usarse para evaluar un modelo trazando una curva característica del operador receptor (ROC) que compara la TPR y la FPR para cada valor de umbral posible entre 0,0 y 1,0:
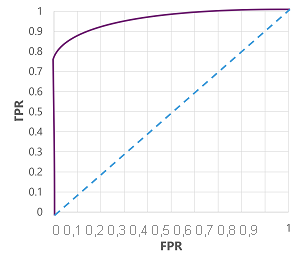
La curva ROC de un modelo perfecto subiría directamente hasta el eje de TPR a la izquierda y después cruzaría el eje de FPR en la parte superior. Dado que el área de trazado de la curva mide 1x1, el área debajo de esta curva perfecta sería 1,0 (lo que significa que el modelo acierta el 100 % del tiempo). Por el contrario, una línea diagonal desde abajo a la izquierda hasta arriba a la derecha representa los resultados que se obtendrían adivinando al azar una etiqueta binaria; produciendo un área bajo la curva de 0,5. En otras palabras, dadas dos etiquetas de clase posibles, podría esperar adivinar correctamente el 50 % del tiempo.
En el caso de nuestro modelo de diabetes, se produce la curva anterior, y la métrica área bajo la curva (AUC) es de 0,875. Dado que el AUC es superior a 0,5, podemos concluir que el modelo funciona mejor al predecir si un paciente tiene diabetes o no que al adivinar aleatoriamente.