¿Qué es la superposición en la computación cuántica?
Si el gato de la unidad anterior fuera un gato cuántico, el estado de este y el sistema de la caja sería el mismo: la suma de las seis posiciones distintas del gato cuántico con respecto a la caja, ponderada por la probabilidad de encontrar el gato cuántico en esa posición. La única diferencia es que el gato clásico puede estar en una (y solo una) de seis posiciones posibles, mientras que el gato cuántico puede estar en las seis posiciones al mismo tiempo.
En el mundo clásico, los objetos solo pueden estar en un estado a la vez. Sin embargo, en el mundo cuántico, las partículas cuánticas pueden estar en varios estados al mismo tiempo. Este fenómeno se denomina superposición.
Por desgracia, en la computación cuántica nadie usa gatos cuánticos, sino cúbits. La palabra "cúbit" significa "bit cuántico". Al igual que en la computación clásica, donde la unidad básica de información es el bit, en la computación cuántica la unidad básica de información es el cúbit. Y al igual que el bit puede tomar dos valores posibles, 0 y 1, un cúbit es cualquier partícula cuántica que pueda estar en dos estados posibles. Por ejemplo, un cúbit podría ser un fotón, que se puede polarizar en dos direcciones, o un electrón, que puede estar en dos niveles de energía.
¿Cómo puede representar la superposición en un cúbit? ¿Qué probabilidad hay de encontrar un cúbit en un estado determinado?
¿Cómo puede representar la superposición en un cúbit?
Un cúbit es una partícula cuántica que tiene dos posiciones posibles o estados. De forma análoga al bit clásico, los estados cuánticos de un cúbit se denominan $0$ y $1$. Un cúbit puede estar en el estado $0$, en el estado $1$ y en cualquier superposición de ambos estados. ¿Cómo puede representar esta superposición?
Imagine que dibuja un círculo y unos ejes vertical y horizontal tales que el punto medio es el centro del círculo. El estado $0$ se coloca en el punto superior del eje vertical y el estado $1$, en el punto inferior.
¿Cómo podría describir esta representación? Podría decir que el estado $0$ es una flecha o un vector, que apunta hacia arriba, y el estado $1$ es un vector que apunta hacia abajo. Por lo tanto, un bit clásico sería un vector que apunta hacia arriba o hacia abajo, pero nunca en otra dirección.
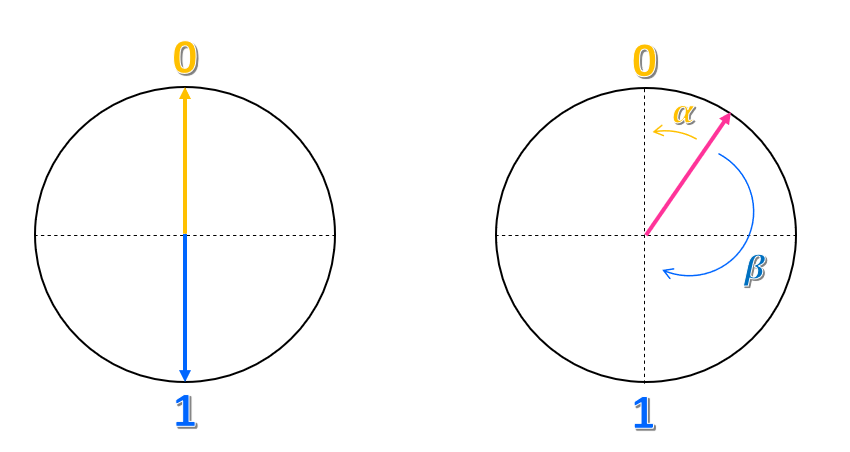
¿Qué hay de cualquier otro punto del círculo? ¿Cómo puede representar ese estado? Al igual que las coordenadas de un plano, podría intentar representarlo como una combinación de los dos estados $0$ y $1$. Por ejemplo, podría tomar lo cerca que está el vector del estado $0$ y llamar a este ángulo $\alpha$, y lo cerca que está del estado $1$ y llamar a este ángulo $\beta$. Podríamos representar el estado como $\alpha 0 + \beta 1 $. Por lo tanto, el estado es una superposición de los estados $0$ y $1$.
Al igual que el ejemplo del gato y la caja, el estado global de un cúbit es la suma de los estados individuales, $0$ y $1$, ponderados por la probabilidad de encontrar el cúbit en ese estado, $\alpha$ y $\beta $.
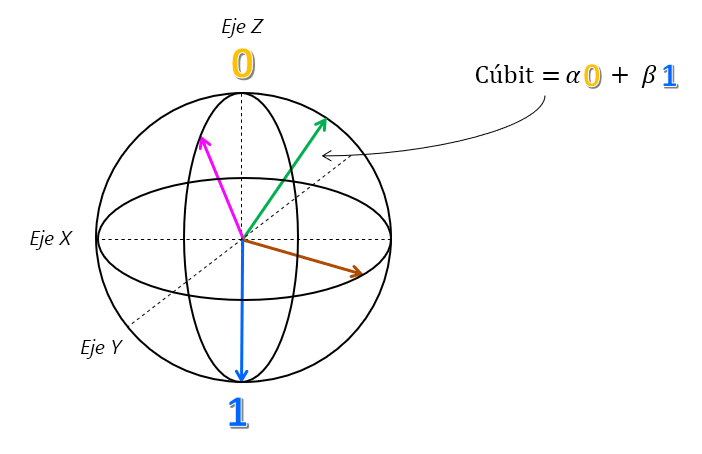
Esta representación de un cúbit es realmente precisa y se conoce como la esfera de Bloch.
Sugerencia
La esfera de Bloch es una herramienta eficaz, ya que las operaciones que podemos realizar en un cúbit pueden representarse como rotaciones en torno a uno de los ejes cardinales. Aunque es muy tentador pensar en un cálculo cuántico como en una secuencia de rotaciones, es un reto utilizar esa noción para diseñar y describir algoritmos. Q# alivia este problema proporcionando un lenguaje para describir estas rotaciones.
¿Cuál es la probabilidad de encontrar un cúbit en un estado?
Al igual que el ejemplo del gato y la caja de la unidad anterior, el estado global de un cúbit es la suma de los estados individuales, $0$ y $1$, ponderados por la probabilidad de encontrar el cúbit en ese estado, $\alpha$ y $\beta $. Los números $\alpha$ y $\beta$ representan lo "cerca" que está el estado del cúbit de los estados $0$ y $1$, respectivamente. Por lo tanto, ¿son $\alpha$ y $\beta$ la probabilidad de encontrar el cúbit en el estado $0$ o $1$? No exactamente.
Los números $\alpha$ y $\beta$ son amplitudes de probabilidad para cada estado. Sus valores absolutos, por ejemplo $|\alpha|^2$ proporcionan las probabilidades correspondientes. Por ejemplo, la probabilidad de observar el estado $0$ es $|\alpha|^2$, y la probabilidad de observar el estado $1$ es $|\beta|^2$.
Los números $\alpha$ y $\beta$ pueden ser números positivos, negativos o incluso complejos. Sin embargo, en una superposición cuántica válida, todas las probabilidades deben sumar uno: $|\alpha|^2+|\beta|^2=1$. Esta restricción se conoce como condición de normalización. Puede pensar en la condición de normalización como el hecho de que siempre obtiene un resultado al medir, de modo que las probabilidades de medir cada resultado posible deben sumar uno.