Ejercicio: Creación de un entrelazamiento cuántico con Q#
En la unidad anterior, ha aprendido sobre el concepto de entrelazamiento cuántico y los estados de Bell.
Ahora, vamos a crear un entrelazamiento cuántico mediante Q# y Quantum Development Kit de Azure. Para crear entrelazamiento, debe aplicar dos operaciones cuánticas: la puerta Hadamard y la puerta Controlled-NOT (CNOT).
Operación Controlled-NOT (CNOT)
Cuando dos cúbits están entrelazados, el estado de un cúbit depende del estado del otro cúbit. Por lo tanto, para entrelazar dos cúbits, necesita una operación que actúe en ambos cúbits al mismo tiempo. Esto se denomina operación de varios cúbits.
Para crear un entrelazamiento cuántico, necesita la operación multiqubit CNOT , que significa Controlled-NOT. Esta operación toma dos cúbits como entrada, una actúa como cúbit de control y la otra es el target cúbit. La operación CNOT invierte el estado del segundo cúbit (el cúbit target) si, y solo si, el estado del primer cúbit (el cúbit de control) es $|1\rangle$.
| Entrada | Salida |
|---|---|
| $\ket{00}$ | $\ket{00}$ |
| $\ket{01}$ | $\ket{01}$ |
| $\ket{10}$ | $\ket{11}$ |
| $\ket{11}$ | $\ket{10}$ |
En Q#, la CNOT operación actúa en una matriz de dos cúbits y voltea el segundo cúbit si el primer cúbit es One.
Entrelazamiento con una operación CNOT
Al aplicar la operación Hadamard, H, y la operación Controlled-NOT, CNOT, puede transformar dos cúbits en el estado $|00\rangle$ al estado Bell $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.
Así es como funciona:
Tome dos cúbits en el estado $|00\rangle$. El primer cúbit es el cúbit de control y el segundo cúbit es el target cúbit.
Cree un estado de superposición solo en el cúbit de control aplicando $H$.
$$H |0_c\rangle={2}}\frac{1}{\sqrt{(|0_c\rangle+|1_c)\rangle$$
Sugerencia
Los subíndices ${}_c$ y ${}_t$ especifican el control y target los cúbits.
Aplique el $operador CNOT$ al cúbit de control, que se encuentra en un estado de superposición y el target cúbit, que se encuentra en el estado $|0_t\rangle$.
$$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c}+\ket{1_c)\ket{0}_t= } CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}+|\ket{1_c 0_t})=\frac{$${1}{\sqrt=$$2}(CNOT \ket{0_c 0_t} + CNOT \ket{1_c 0_t})$$\frac{1}{\sqrt$$==2}(\ket{0_c 0_t}+\ket{1_c 1_t)}$$
Creación de un nuevo archivo Q#
- Abra Visual Studio Code.
- Seleccione Archivo > Nuevo archivo de texto y guárdelo como Main.qs.
- Seleccione Ver> - Paleta de comandos y escriba Q#: Establezca el targetperfil de QIR de Azure Quantum. Presione ENTRAR.
- Seleccione Q#: Sin restricciones.
Crear el estado de Campana $\ket{\phi^+}$
Comencemos creando el estado $\ket{\phide Campana ^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.
En primer lugar, debe importar el espacio de nombres
Microsoft.Quantum.Diagnosticsde la biblioteca Estándar, que contiene la funciónDumpMachine. Esta función muestra el estado actual de los cúbits. Copie y pegue el siguiente código Q# en el archivo Main.qs.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;Sugerencia
También puede importar la biblioteca Estándar sustituyendo
Microsoft.QuantumporStd. Por ejemplo,import Std.Diagnostics.*es equivalente aimport Microsoft.Quantum.Diagnostics.*.Cree la operación
Mainque devuelve dos valores de tipoResult, que son los resultados de medición de los cúbits.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { // Your code goes here }Dentro de la operación
Main, usted asigna dos cúbits,q1yq2, que se entrelazarán.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); }Aplique la puerta Hadamard,
H, al primer cúbit,q1, para colocarla en un estado de superposición. A continuación, entrelace los dos cúbits mediante la operaciónCNOT.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); CNOT(q1, q2); }Use la función
DumpMachinepara mostrar el estado actual de los cúbits. Esto no es lo mismo que medir los cúbits.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); CNOT(q1, q2); DumpMachine(); }Mida los cúbits mediante la operación
My almacene los resultados enm1ym2. A continuación, use la operaciónResetpara restablecer los cúbits. En Q#, siempre debe restablecer los cúbits al estado $|0\rangle$.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); CNOT(q1, q2); DumpMachine(); let (m1, m2) = (M(q1), M(q2)); Reset(q1); Reset(q2); }Por último, devuelva los resultados de medición de los cúbits con la instrucción
return. El archivo Main.qs debe tener este aspecto:import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); CNOT(q1, q2); DumpMachine(); let (m1, m2) = (M(q1), M(q2)); Reset(q1); Reset(q2); return (m1, m2); }Para ejecutar el programa en el simulador integrado, haga clic en Ejecutar encima de la operación
Maino presione Ctrl+F5. La salida aparecerá en la consola de depuración.Los resultados de la medición se correlacionan, por lo que al final del programa se obtiene un resultado de
(Zero, Zero)o(One, One)con la misma probabilidad.Para visualizar el diagrama del circuito, haga clic en Circuito en la lista de comandos encima de la operación
Main. El diagrama del circuito muestra la puerta Hadamard aplicada al primer cúbit y la puerta CNOT aplicada a ambos cúbits.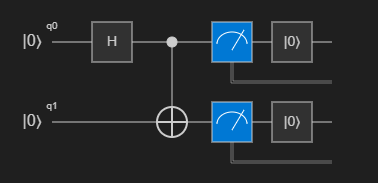
Crear otros estados de Bell
Para crear otros estados de Bell, debe aplicar operaciones adicionales de Pauli $X$ y $Z$ a los cúbits.
Por ejemplo, para crear el estado $\ket{\phide Bell ^-}=\frac1{\sqrt2}(|00-11|\rangle\rangle)$, puede aplicar la operación Pauli $Z$ al cúbit de control después de aplicar la puerta Hadamard. La $operación Z$ voltea el estado $\ket{+}$ a $\ket{-}$.
Sugerencia
Los estados $\frac{{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ y $\frac{1}{\sqrt{{2}}(|0\rangle -|1\rangle)$ también se conocen como $\ket{+}$ y $\ket{{-}$, respectivamente.
Así es como funciona:
Tome dos cúbits en el estado $|00\rangle$.
Cree un estado de superposición solo en el cúbit de control aplicando $H$.
$$H |0_c\frac{\rangle={1}{\sqrt{2}}(|0_c\rangle+1_c\rangle)= \ket{+_c|}$$
Aplique la $operación Z$ al cúbit de control.
$$Z \frac{{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)=\frac{1}{\sqrt{{2}}(|0_c-1_c|\rangle\rangle)_c=\ket{{-}$$
Aplique el $operador CNOT$ al cúbit de control y al target cúbit, que se encuentra en el estado $|0_t\rangle$.
$$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c-1_c}\ket{})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t-1_c 0_t}}|\ket{){1}{\sqrt$$=\frac{=$$2}(CNOT \ket{0_c 0_t} - CNOT \ket{1_c 0_t})$$\frac{1}{\sqrt=$$=2}(\ket{0_c 0_t-1_c 1_t)}\ket{}$$
Del mismo modo, Bell indica $\ket{\psi^+}$ y $\ket{\psi^-}$ se pueden crear aplicando las operaciones Pauli $X$ y $Z$ a los cúbits.
- El estado $\ket{\pside Campana ^+}=\frac1{\sqrt2}(|01\rangle+|10\rangle)$ se puede crear aplicando la operación Pauli $X$ al target cúbit después de aplicar la puerta hadamard.
- El estado $\ket{\psibell ^-}=\frac1{\sqrt2}(|01-10\rangle\rangle|)$ se puede crear aplicando el Pauli $Z$ al cúbit de control y el Pauli $X$ al target cúbit después de aplicar la puerta hadamard.
Crear el estado de Bell $\ket{\phi^+}$ en Q#
Modifique el Q# código para crear el estado de $\ket{\phiBell ^-}$. El archivo Main.qs debe tener este aspecto:
import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); Z(q1); // Apply the Pauli Z operation to the control qubit CNOT(q1, q2); DumpMachine(); let (m1, m2) = (M(q1), M(q2)); Reset(q1); Reset(q2); return (m1, m2); }Para ejecutar el programa en el simulador integrado, haga clic en Ejecutar encima de la operación
Maino presione Ctrl+F5. La salida aparecerá en la consola de depuración.Para visualizar el diagrama del circuito, haga clic en Circuito en la lista de comandos encima de la operación
Main. El diagrama del circuito muestra la puerta Hadamard aplicada al primer cúbit, la puerta de Pauli $Z$ aplicada al primer cúbit y la puerta CNOT aplicada a ambos cúbits.
En la siguiente unidad, aprenderá a usar el entrelazamiento para teletransportar información cuántica.