Visualización de gráficos en cuadernos
La visualización de datos es un aspecto clave de la exploración de datos. Implica presentar datos en un formato gráfico, lo que hace que los datos complejos sean más comprensibles y utilizables.
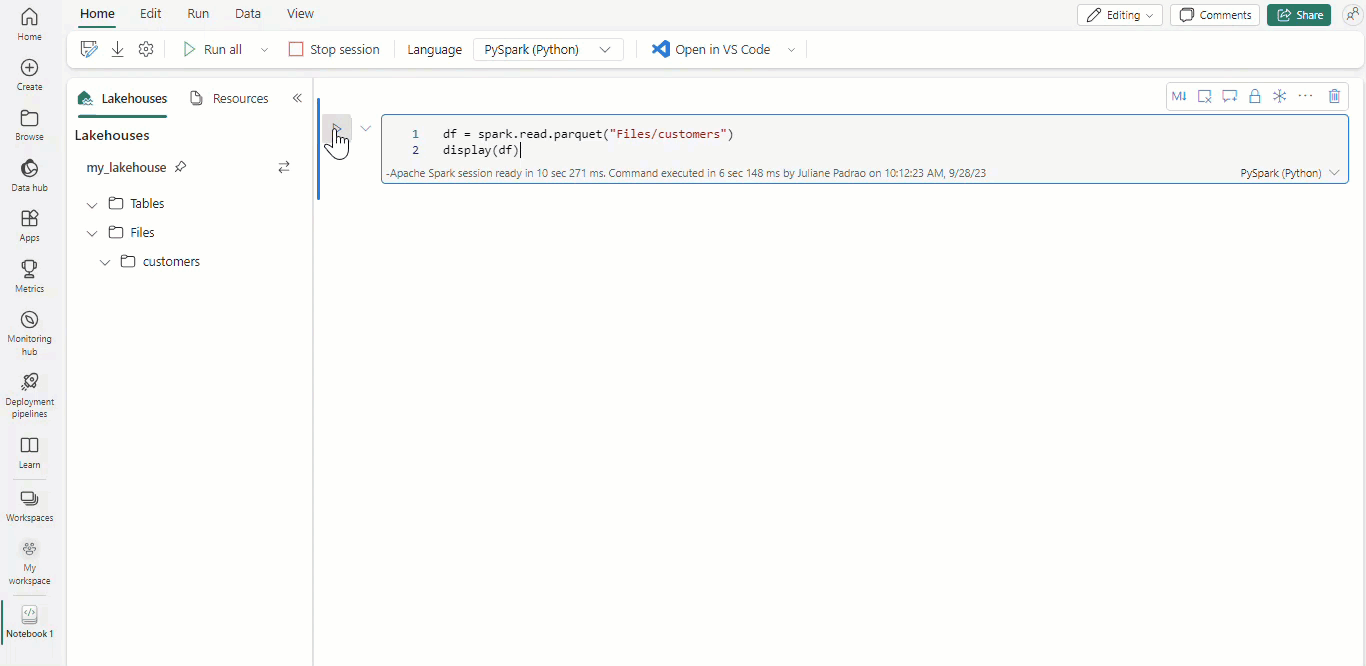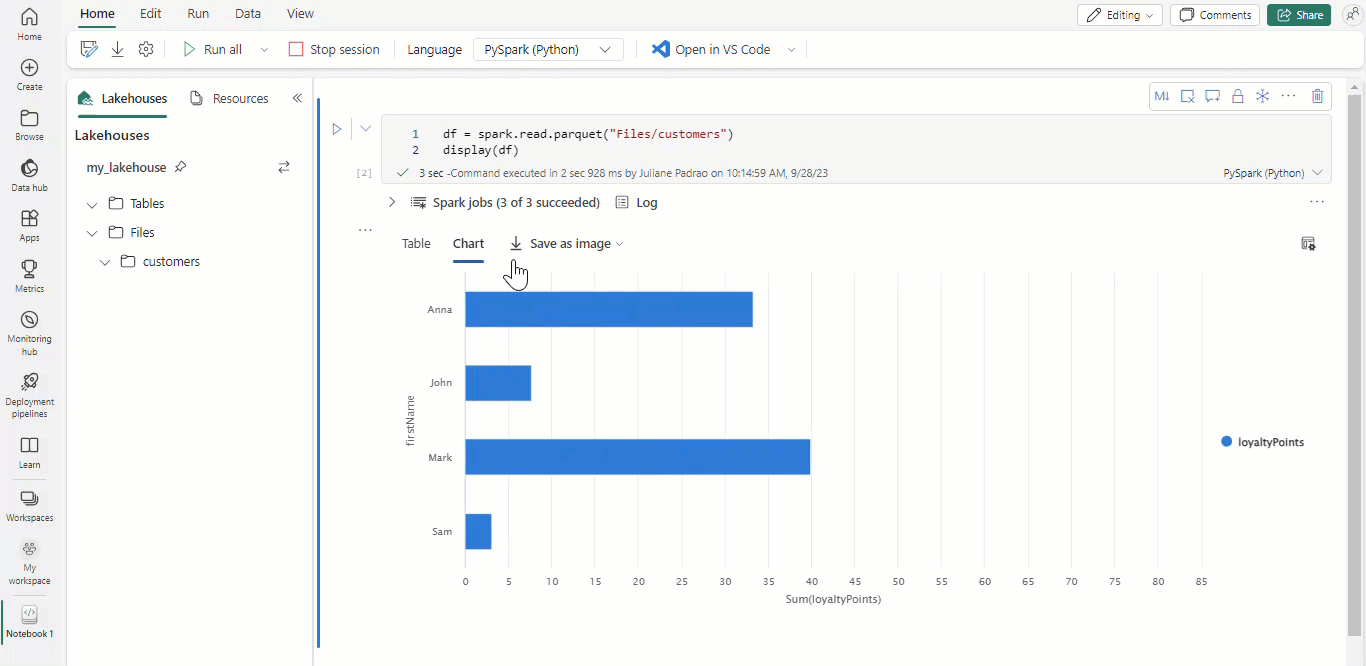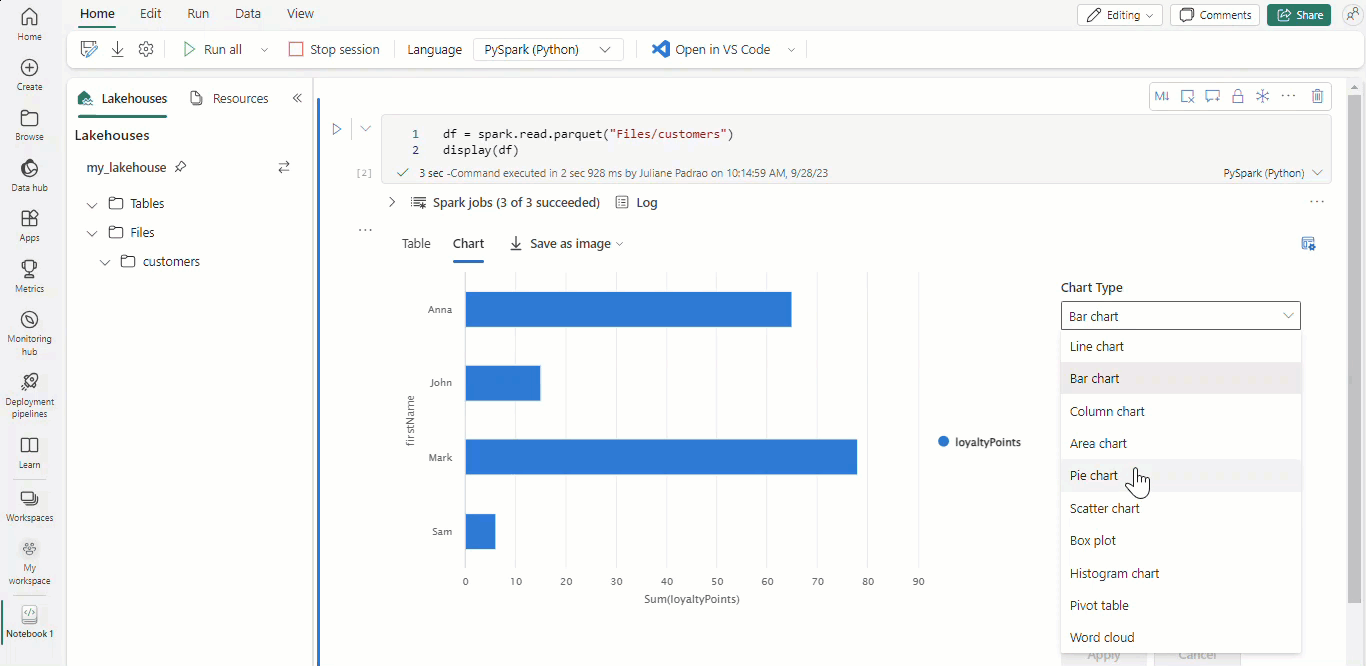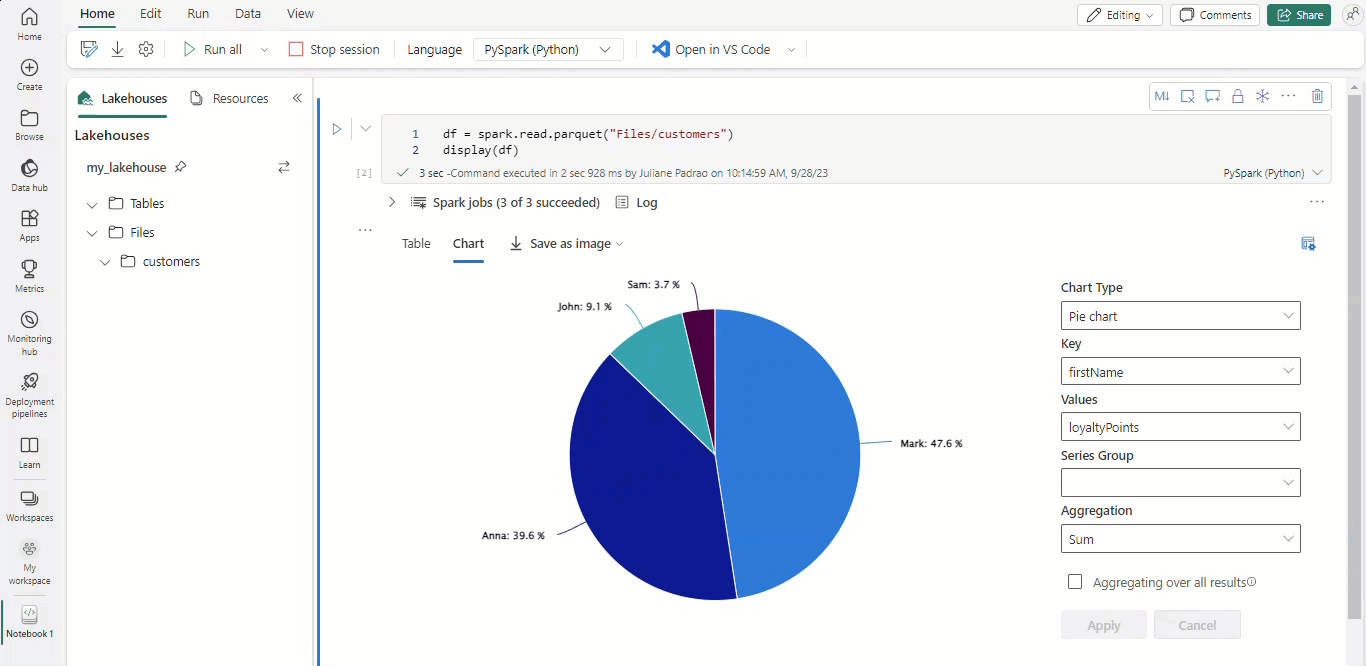
Con los cuadernos de Microsoft Fabric y los dataframes de Apache Spark, los resultados tabulares se presentan automáticamente como gráficos sin necesidad de codificación adicional.
Sugerencia
También se pueden usar bibliotecas de código abierto como matplotlib y plotly entre otras para mejorar la experiencia de exploración de datos.
Comprensión de las variables numéricas y categóricas
En el caso de las variables categóricas, es importante comprender las diferentes categorías o niveles de la variable. Esto implica identificar cuántas observaciones hay en cada categoría, lo que se conoce como recuentos o frecuencias. Además, comprender qué proporción o porcentaje de las observaciones representa cada categoría es fundamental.
Cuando se trata de variables numéricas, es necesario tener en cuenta varios aspectos. La tendencia central de la variable, que puede ser la media, la mediana o el modo, proporciona un resumen de la variable.
Las medidas de dispersión, como el rango, el rango intercuartil (IQR), la desviación estándar o la varianza proporcionan información sobre la propagación de la variable. Por último, comprender la distribución de la variable es clave. Esto implica determinar si la variable se distribuye normalmente o sigue alguna otra distribución e identifica los valores atípicos.
A menudo se conocen como estadísticas de resumen de variables numéricas y categóricas.
Estadísticas de resumen
Las estadísticas de resumen están disponibles para los dataframes de Apache Spark cuando se usa el parámetro summary=True.
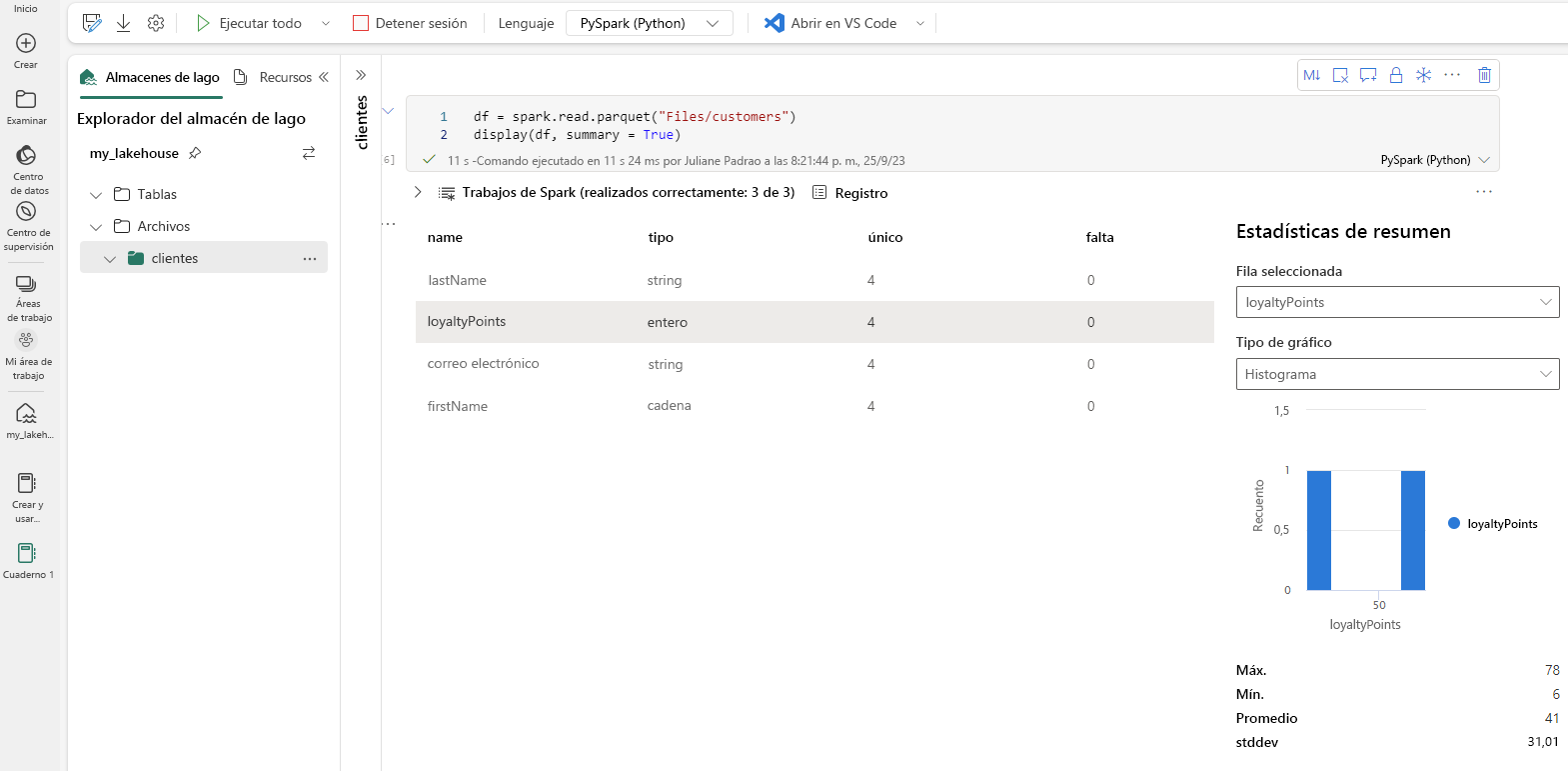
Como alternativa, puede generar las estadísticas de resumen mediante Python.
import pandas as pd
df = pd.DataFrame({
'Height_in_cm': [170, 180, 175, 185, 178],
'Weight_in_kg': [65, 75, 70, 80, 72],
'Age_in_years': [25, 30, 28, 35, 32]
})
desc_stats = df.describe()
print(desc_stats)
Análisis univariante
El análisis univariante es la forma más sencilla de análisis de datos donde los datos que se analizan contienen solo una variable. El propósito principal del análisis univariante es describir los datos y buscar patrones en ellos.
Estos son trazados comunes que se usan para realizar análisis univariantes.
Histogramas: Se usa para mostrar la frecuencia de cada categoría de una variable continua. Pueden ayudar a identificar la tendencia central, la forma y la propagación de los datos.
Diagramas de cajas: Se usa para mostrar el rango, el rango intercuartil (IQR), la mediana y los valores atípicos potenciales de una variable numérica.
Gráficos de barras: Son similares a los histogramas, pero normalmente se usan para variables categóricas. Cada barra representa una categoría y la altura o longitud de la barra corresponde a su frecuencia o proporción.
El código siguiente crea un diagrama de cajas y un histograma mediante Python.
import numpy as np
import matplotlib.pyplot as plt
# Let's assume these are the heights of a group in inches
heights_in_inches = [63, 64, 66, 67, 68, 69, 71, 72, 73, 55, 75]
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
# Boxplot
axs[0].boxplot(heights_in_inches, whis=0.5)
axs[0].set_title('Box plot of heights')
# Histogram
bins = range(min(heights_in_inches), max(heights_in_inches) + 5, 5)
axs[1].hist(heights_in_inches, bins=bins, alpha=0.5)
axs[1].set_title('Frequency distribution of heights')
axs[1].set_xlabel('Height (in)')
axs[1].set_ylabel('Frequency')
plt.tight_layout()
plt.show()
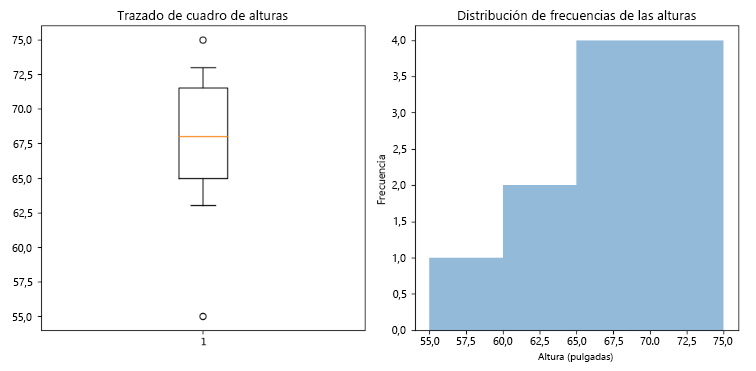
Estas son algunas conclusiones que podemos extraer de los resultados.
- En el diagrama de cajas, la distribución de alturas está sesgada a la izquierda, lo que significa que hay muchas personas con alturas significativamente por debajo de la media.
- Hay dos valores atípicos potenciales: 55 pulgadas (4'7") y 75 pulgadas (6'3"). Estos valores son inferiores y superiores al resto de puntos de datos.
- La distribución de alturas es aproximadamente simétrica alrededor de la mediana, suponiendo que los valores atípicos no sesguen significativamente la distribución.
Análisis bivariante y multivariante
El análisis bivariante y multivariante ayuda a comprender las relaciones y las interacciones entre diferentes variables de un conjunto de datos y a menudo se presentan mediante gráficos de dispersión, matrices de correlación o tabulaciones cruzadas.
Gráficos de dispersión
El código siguiente usa la función scatter() de matplotlib para crear el gráfico de dispersión. Se especifica house_sizes para el eje X y house_prices para el eje Y.
import matplotlib.pyplot as plt
import numpy as np
# Sample data
np.random.seed(0) # for reproducibility
house_sizes = np.random.randint(1000, 3000, size=50) # Size of houses in square feet
house_prices = house_sizes * 100 + np.random.normal(0, 20000, size=50) # Price of houses in dollars
# Create scatter plot
plt.scatter(house_sizes, house_prices)
# Set plot title and labels
plt.title('House Prices vs Size')
plt.xlabel('Size (sqt)')
plt.ylabel('Price ($)')
# Display the plot
plt.show()
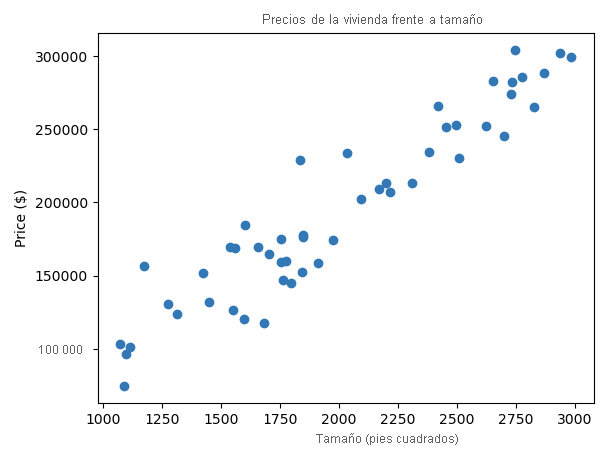
En este gráfico de dispersión, cada punto representa una casa. Verá que a medida que aumenta el tamaño de la casa (moverse a la derecha a lo largo del eje X), el precio también tiende a aumentar (moverse hacia arriba a lo largo del eje Y).
Este tipo de análisis nos ayuda a comprender cómo afectan los cambios en las variables dependientes a la variable de destino. Al analizar las relaciones entre estas variables, podemos realizar predicciones sobre la variable de destino en función de los valores de las variables dependientes.
Además, este análisis puede ayudar a identificar qué variables dependientes tienen un impacto significativo en la variable de destino. Esto es útil para la selección de características en los modelos de aprendizaje automático, donde el objetivo es usar las características más relevantes para predecir el destino.
Diagrama de líneas
El siguiente script de Python usa la biblioteca matplotlib para crear un diagrama de líneas de precios de casas simulados durante un período de tres años. Genera una lista de fechas mensuales de 2020 a 2022 y una lista correspondiente de precios de casas, que comienzan desde $200.000 y aumentan cada mes con cierta aleatoriedad.
El eje X del diagrama está creado para mostrar fechas en formato "Año-Mes" y establecer el intervalo de tics del eje X en cada seis meses.
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
import random
import matplotlib.dates as mdates
# Generate monthly dates from 2020 to 2022
dates = [datetime(2020, 1, 1) + timedelta(days=30*i) for i in range(36)]
# Generate corresponding house prices with some randomness
prices = [200000 + 5000*i + random.randint(-5000, 5000) for i in range(36)]
plt.figure(figsize=(10,5))
# Plot data
plt.plot(dates, prices)
# Format x-axis to display dates
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
plt.gca().xaxis.set_major_locator(mdates.MonthLocator(interval=6)) # set interval to 6 months
plt.gcf().autofmt_xdate() # Rotation
# Set plot title and labels
plt.title('House Prices Over Years')
plt.xlabel('Year-Month')
plt.ylabel('House Price ($)')
# Show the plot
plt.show()
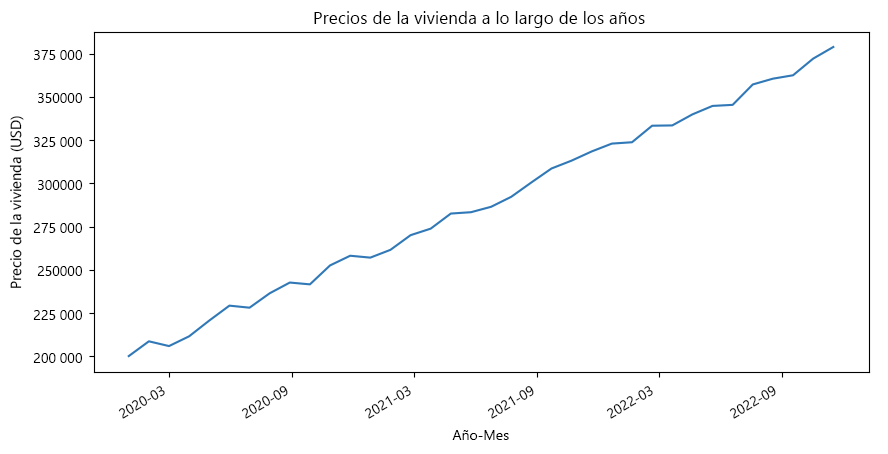
Los diagramas de línea son fáciles de entender y leer. Proporcionan una visión general clara y de alto nivel de la progresión de los datos a lo largo del tiempo, por lo que son una opción popular para los datos de series temporales.
Diagrama por pares
Un diagrama por pares puede ser útil cuando se desea visualizar la relación entre varias variables a la vez.
import seaborn as sns
import pandas as pd
# Sample data
data = {
'Size': [1000, 2000, 3000, 1500, 1200],
'Bedrooms': [2, 4, 3, 2, 1],
'Age': [5, 10, 2, 6, 4],
'Price': [200000, 400000, 350000, 220000, 150000]
}
df = pd.DataFrame(data)
# Create a pair plot
sns.pairplot(df)
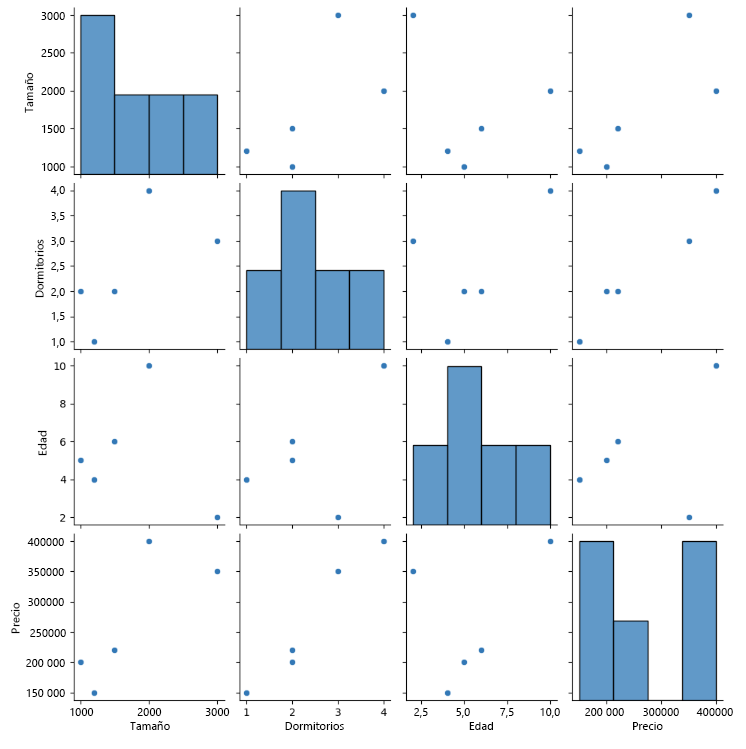
Esto crea una cuadrícula de trazados donde cada característica se traza en todas las demás características. En la diagonal hay histogramas que muestran la distribución de cada característica. Los trazados fuera de diagonal son gráficos de dispersión que muestran la relación entre dos características.
Este tipo de visualización puede ayudarnos a comprender cómo se relacionan las diferentes características entre sí y podría usarse para informar a las decisiones sobre la compra o venta de casas.