Descripción de la distribución de datos
Comprender la distribución de los datos es esencial para el análisis de datos, la visualización y la creación de modelos eficaces.
Si un conjunto de datos tiene una distribución sesgada, significa que los puntos de datos no se distribuyen uniformemente y tienden a inclinarse más hacia la derecha o hacia la izquierda. Esto puede provocar que un modelo prediga inexactamente los puntos de datos de grupos infrarrepresentados o se optimice en función de una métrica inapropiada.
La importancia de la distribución de datos
A continuación se muestran áreas clave en las que comprender la distribución de los datos puede mejorar la precisión de los modelos de aprendizaje automático.
| Paso | Descripción |
|---|---|
| Análisis exploratorio de datos (EDA) | Comprender la distribución de datos facilita la exploración de un nuevo conjunto de datos y la búsqueda de patrones. |
| Preprocesamiento de datos | Algunas técnicas de preprocesamiento, como la normalización o la estandarización, se usan para hacer que los datos se distribuyan con más normalidad, que es una suposición común en muchos modelos. |
| Selección de modelos | Los diferentes modelos hacen diferentes suposiciones sobre la distribución de los datos. Por ejemplo, algunos modelos asumen que los datos se distribuyen normalmente y que pueden no funcionar bien si se infringe esta suposición. |
| Mejora del rendimiento del modelo | Transformar la variable de destino para reducir la asimetría puede linealizar el destino, lo que resulta útil para muchos modelos. Esto puede reducir el intervalo del error y mejorar potencialmente el rendimiento del modelo. |
| Relevancia del modelo | Una vez implementado un modelo en producción, es importante que siga siendo relevante en el contexto de los datos más recientes. Si hay una asimetría de datos, es decir, los cambios de distribución de datos en producción de lo que se usó durante el entrenamiento, el modelo puede salirse del contexto. |
Comprender la distribución de datos puede mejorar el proceso de creación de modelos. Le permite establecer suposiciones más precisas mediante la identificación del promedio, la propagación y el intervalo de una variable aleatoria en las características y el destino.
Vamos a explorar algunos de los tipos de distribución de datos más comunes, como las distribuciones normales, binomiales y uniformes.
Distribución normal
Una distribución normal se representa mediante dos parámetros: la media y la desviación estándar. La media indica dónde se centra la curva de campana y la desviación estándar indica la propagación de la distribución.
Veamos un ejemplo de una característica distribuida normal. El código siguiente genera los datos para la característica var con fines de demostración.
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
# Set the mean and standard deviation
mu, sigma = 0, 0.1
# Generate a normally distributed variable
var = np.random.normal(mu, sigma, 1000)
# Create a histogram of the variable using seaborn's histplot
sns.histplot(var, bins=30, kde=True)
# Add title and labels
plt.title('Histogram of Normally Distributed Variable')
plt.xlabel('Value')
plt.ylabel('Frequency')
# Show the plot
plt.show()
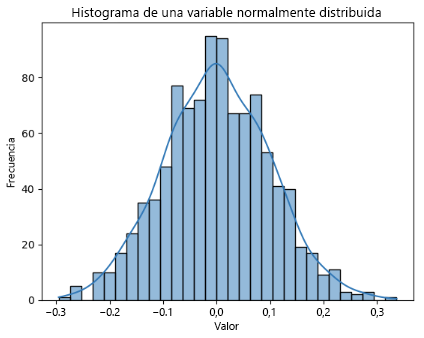
Observe que la característica var se distribuye normalmente, donde se espera que la media y la mediana (percentil 50 %) sean más o menos iguales. En distribuciones sesgadas, la media tiende a inclinarse hacia la cola más pesada.
Sin embargo, estas son comprobaciones heurísticas y la determinación real se realizan mediante pruebas estadísticas específicas como Shapiro-Wilk o Kolmogorov-Smirnov para la normalidad.
Distribución binomial
Supongamos que desea comprender cómo de bien se observa una característica determinada en un grupo de pingüinos.
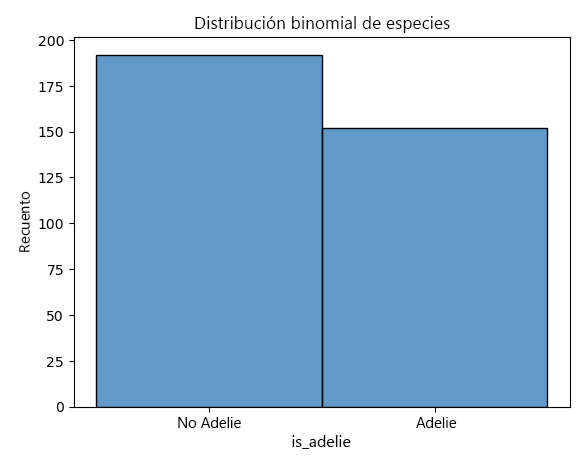
Decide examinar un conjunto de datos de 200 pingüinos para ver si son de la especie Adelie. Se trata de un problema de distribución binomial porque hay dos posibles resultados (Adelie o no Adelie), un número fijo de ensayos (200 pingüinos) y cada ensayo es independiente de los otros.
Tras analizar el conjunto de datos, se observa que 150 pingüinos son de la especie Adelie.
Saber que los datos siguen una distribución binomial le permite realizar predicciones sobre futuros conjuntos de datos o grupos de pingüinos. Por ejemplo, si estudia otro grupo de 200 pingüinos, puede esperar que alrededor de 150 sean de la especie Adelie.
El siguiente código de Python traza un histograma de la variable binomial is_adelie. El argumento discrete=True de sns.histplot garantiza que los intervalos se tratan como intervalos discretos. Esto significa que cada barra del histograma corresponde exactamente a una categoría o valor booleano, lo que facilita la interpretación del trazado.
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
# Load the Penguins dataset from seaborn
penguins = sns.load_dataset('penguins')
# Create a binomial variable for 'species'
penguins['is_adelie'] = np.where(penguins['species'] == 'Adelie', 1, 0)
# Plot the distribution of 'is_adelie'
sns.histplot(data=penguins, x='is_adelie', bins=2, discrete=True)
plt.title('Binomial Distribution of Species')
plt.xticks([0, 1], ['Not Adelie', 'Adelie'])
plt.show()
Distribución uniforme
Una distribución uniforme, también conocida como distribución rectangular, es un tipo de distribución de probabilidad en la que todos los resultados son igualmente probables. Cada intervalo de la misma longitud en la compatibilidad de la distribución tiene la misma probabilidad.
import numpy as np
import matplotlib.pyplot as plt
# Generate a uniform distribution
uniform_data = np.random.uniform(-1, 1, 1000)
# Plot the distribution
plt.hist(uniform_data, bins=20, density=True)
plt.title('Uniform Distribution')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()
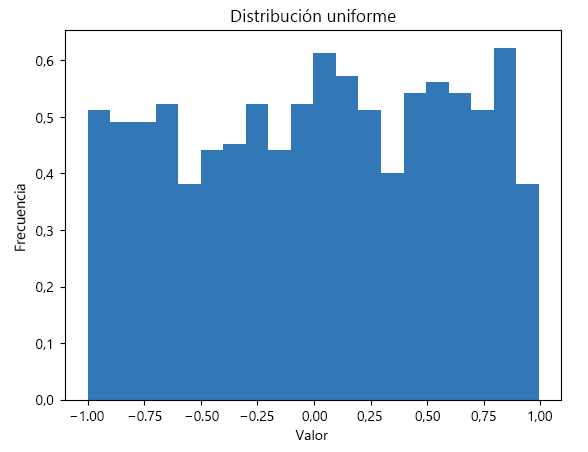
En este código, la función np.random.uniform genera 1000 números aleatorios distribuidos uniformemente entre -1 y 1. El argumento bins=30 especifica que los datos deben dividirse en 30 cubos y density=True garantiza que el histograma se normalice para formar una densidad de probabilidad. Esto significa que el área debajo del histograma se integra en 1, lo que resulta útil al comparar distribuciones.
Nota:
Es probable que obtenga resultados diferentes si ejecuta el código varias veces. La idea básica de la aleatoriedad es que es impredecible y cada vez que muestrea, puede obtener resultados diferentes.
Puede controlar este proceso estableciendo un valor de inicialización con np.random.seed. Esto es muy útil para probar y depurar en la fase de creación de modelos, ya que permite reproducir los mismos resultados.