Imágenes y procesamiento de imágenes
Antes de explorar el procesamiento de imágenes y otras posibilidades de la visión por ordenador, conviene considerar qué es realmente una imagen en el contexto de los datos para un programa informático.
Imágenes como matrices de píxel
En un equipo, una imagen es una matriz de valores numéricos de píxeles. Por ejemplo, considere la siguiente matriz:
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 255 255 255 0 0
0 0 255 255 255 0 0
0 0 255 255 255 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
La matriz consta de siete filas y siete columnas, que representan los valores de píxel de una imagen de 7x7 píxeles (que se conoce como la resolución de la imagen). Cada píxel tiene un valor comprendido entre 0 (negro) y 255 (blanco); los valores entre estos límites representan tonos de gris. La imagen representada por esta matriz es similar a la siguiente imagen (magnificada):

La matriz de valores de píxeles de esta imagen es bidimensional (representa filas y columnas, o coordenadas x e y) y define un único rectángulo de valores de píxeles. Una sola capa de valores de píxeles como esta representa una imagen de escala de grises. En realidad, la mayoría de las imágenes digitales son multidimensionales y constan de tres capas (conocidas como canales) que representan los tonos de color rojo, verde y azul (RGB). Por ejemplo, podríamos representar una imagen a color definiendo tres canales de valores de pixel que creen la misma forma cuadrada que el ejemplo anterior en escala de grises:
Red:
150 150 150 150 150 150 150
150 150 150 150 150 150 150
150 150 255 255 255 150 150
150 150 255 255 255 150 150
150 150 255 255 255 150 150
150 150 150 150 150 150 150
150 150 150 150 150 150 150
Green:
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 255 255 255 0 0
0 0 255 255 255 0 0
0 0 255 255 255 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
Blue:
255 255 255 255 255 255 255
255 255 255 255 255 255 255
255 255 0 0 0 255 255
255 255 0 0 0 255 255
255 255 0 0 0 255 255
255 255 255 255 255 255 255
255 255 255 255 255 255 255
Esta es la imagen resultante:

Los cuadrados púrpuras se representan mediante la combinación:
Red: 150
Green: 0
Blue: 255
Los cuadrados amarillos del centro se representan mediante la combinación:
Red: 255
Green: 255
Blue: 0
Uso de filtros para procesar imágenes
Una manera común de realizar tareas de procesamiento de imágenes es aplicar filtros que modifican los valores de píxel de la imagen para crear un efecto visual. Un filtro se define mediante una o varias matrices de valores de píxel, denominados kernels de filtro. Por ejemplo, podría definir el filtro con un kernel 3x3 como se muestra en este ejemplo:
-1 -1 -1
-1 8 -1
-1 -1 -1
A continuación, el kernel se convoluciona a través de la imagen, calculando una suma ponderada para cada revisión de 3x3 píxeles y asignando el resultado a una nueva imagen. Es más fácil entender cómo funciona el filtrado explorando un ejemplo paso a paso.
Empecemos con la imagen en escala de grises que exploramos anteriormente:
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 255 255 255 0 0
0 0 255 255 255 0 0
0 0 255 255 255 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
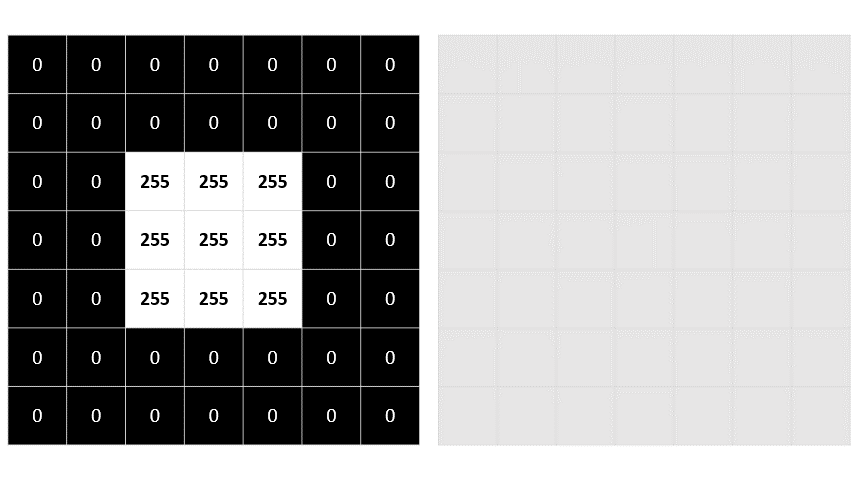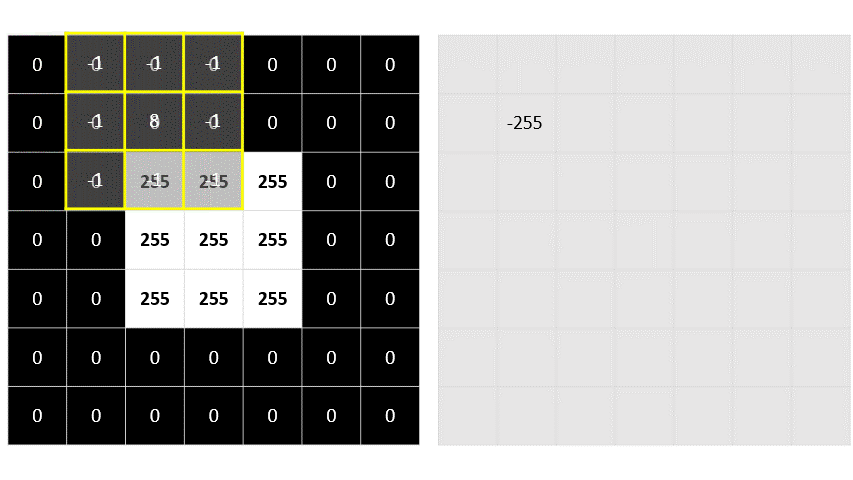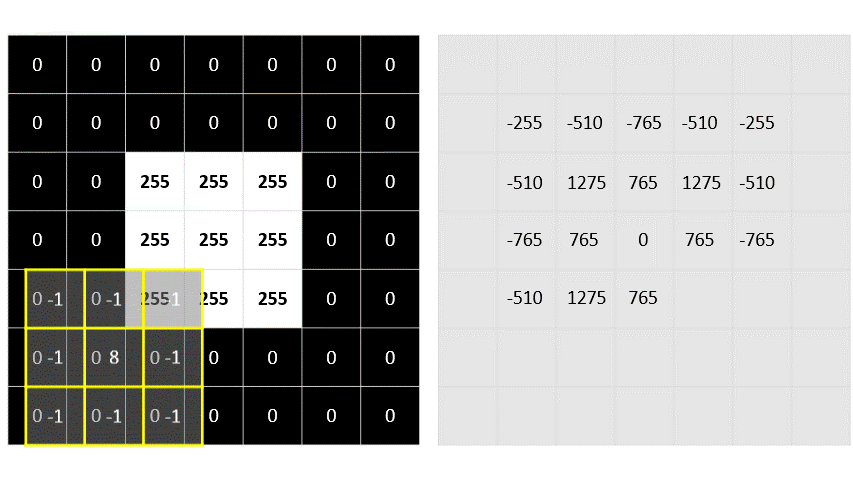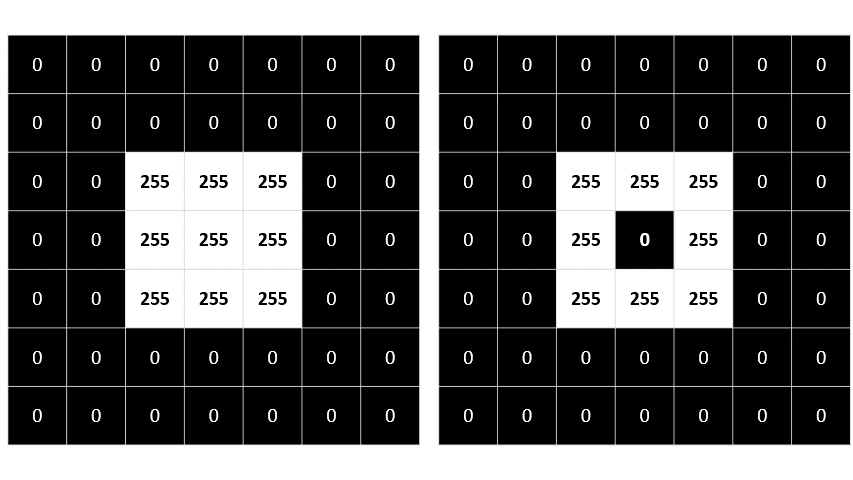
En primer lugar, aplicamos el kernel del filtro a la revisión superior izquierda de la imagen, multiplicando el valor de cada píxel por el valor de peso correspondiente en el kernel y agregando los resultados:
(0 x -1) + (0 x -1) + (0 x -1) +
(0 x -1) + (0 x 8) + (0 x -1) +
(0 x -1) + (0 x -1) + (255 x -1) = -255
El resultado (-255) se convierte en el primer valor de una nueva matriz. A continuación, movemos el kernel del filtro un píxel hacia la derecha y repetimos la operación:
(0 x -1) + (0 x -1) + (0 x -1) +
(0 x -1) + (0 x 8) + (0 x -1) +
(0 x -1) + (255 x -1) + (255 x -1) = -510
De nuevo, el resultado se agrega a la nueva matriz, que ahora contiene dos valores:
-255 -510
El proceso se repite hasta que el filtro se ha convolucionado en toda la imagen, como se muestra en esta animación:
El filtro se convoluciona a través de la imagen, calculando una nueva matriz de valores. Algunos de los valores pueden estar fuera del intervalo de valores de 0 a 255 píxeles, por lo que los valores se ajustan para ajustarse a ese intervalo. Debido a la forma del filtro, no se calcula el borde exterior de los píxeles, por lo que se aplica un valor de relleno (normalmente 0). La matriz resultante representa una nueva imagen en la que el filtro ha transformado la imagen original. En este caso, el filtro ha tenido el efecto de resaltar los bordes de las formas de la imagen.
Para ver más claramente el efecto del filtro, aquí tiene un ejemplo del mismo filtro aplicado a una imagen real:
| Imagen original | Imagen filtrada |
|---|---|
 |
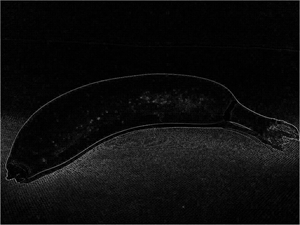 |
Debido a que el filtro se convoluciona a través de la imagen, este tipo de manipulación de la imagen se conoce a menudo como filtrado convolucional. El filtro usado en este ejemplo es un tipo determinado de filtro (denominado filtro laplace) que resalta los bordes de los objetos de una imagen. Hay muchos otros tipos de filtros que se pueden usar para crear desenfoques, dar nitidez, invertir el color y otros efectos.