Tres maneras de dibujar un arco
Obtenga información sobre cómo usar SkiaSharp para definir arcos de tres maneras diferentes
Un arco es una curva en la circunferencia de una elipse, como las partes redondeadas de este signo infinito:
A pesar de la simplicidad de esa definición, no hay forma de definir una función de dibujo de arco que satisfaga todas las necesidades y, por lo tanto, no hay consenso entre los sistemas gráficos de la mejor manera de dibujar un arco. Por este motivo, la clase SKPath no se restringe solo a un enfoque.
SKPath define un método de AddArc, cinco métodos de ArcTo diferentes y dos métodos de RArcTo relativos. Estos métodos se dividen en tres categorías, que representan tres enfoques muy diferentes para especificar un arco. La que usa depende de la información disponible para definir el arco y de cómo encaja este arco con los otros gráficos que está dibujando.
El arco angular
El enfoque de arco angular para dibujar arcos requiere que especifique un rectángulo que enlaza una elipse. El arco de la circunferencia de esta elipse se indica mediante ángulos desde el centro de la elipse que indican el principio del arco y su longitud. Dos métodos diferentes dibujan arcos angulares. Estos son el método AddArc y el método ArcTo:
public void AddArc (SKRect oval, Single startAngle, Single sweepAngle)
public void ArcTo (SKRect oval, Single startAngle, Single sweepAngle, Boolean forceMoveTo)
Estos métodos son idénticos a los métodos Android AddArc y [ArcTo]xref:Android.Graphics.Path.ArcTo*). El método AddArc de iOS es similar, pero está restringido a los arcos de la circunferencia de un círculo en lugar de generalizado a una elipse.
Ambos métodos comienzan con un valor de SKRect que define tanto la ubicación como el tamaño de una elipse:
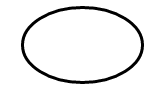
El arco forma parte de la circunferencia de esta elipse.
El argumento startAngle es un ángulo en sentido de las agujas del reloj en grados relativo a una línea horizontal dibujada desde el centro de la elipse a la derecha. El argumento sweepAngle es relativo al startAngle. Estos son startAngle y sweepAngle valores de 60 y 100 grados, respectivamente:
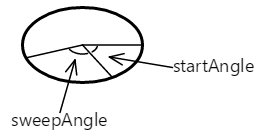
El arco comienza en el ángulo inicial. Su longitud se rige por el ángulo de barrido. El arco se muestra aquí en rojo:
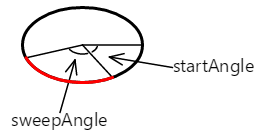
La curva agregada al trazado con el método AddArc o ArcTo es simplemente esa parte de la circunferencia de la elipse:

Los argumentos startAngle o sweepAngle pueden ser negativos: el arco es el sentido de las agujas del reloj para los valores positivos de sweepAngle y en sentido contrario para los valores negativos.
Sin embargo, AddArc no define un contorno cerrado. Si llama a LineTo después de AddArc, se dibuja una línea desde el final del arco hasta el punto del método LineTo y lo mismo es verdadero de ArcTo.
AddArc inicia automáticamente un nuevo contorno y es funcionalmente equivalente a una llamada a ArcTo con un argumento final de true:
path.ArcTo (oval, startAngle, sweepAngle, true);
Ese último argumento se denomina forceMoveTo, y provoca eficazmente una llamada MoveTo al principio del arco. Eso comienza un nuevo contorno. No es el caso con un último argumento de false:
path.ArcTo (oval, startAngle, sweepAngle, false);
Esta versión de ArcTo dibuja una línea desde la posición actual hasta el principio del arco. Esto significa que el arco puede estar en algún lugar en medio de un contorno mayor.
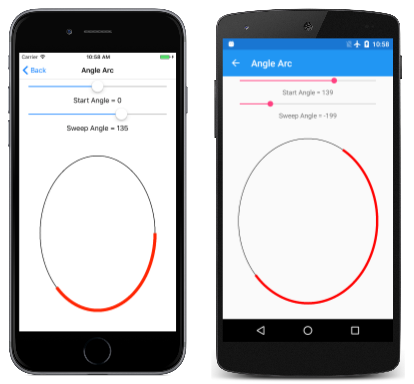
La página Arco angular permite usar dos controles deslizantes para especificar los ángulos de inicio y barrido. El archivo XAML crea una instancia de dos elementos Slider y un SKCanvasView. El controlador PaintCanvas del archivo AngleArcPage.xaml.cs dibuja el óvalo y el arco mediante dos objetos SKPaint definidos como campos:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
SKRect rect = new SKRect(100, 100, info.Width - 100, info.Height - 100);
float startAngle = (float)startAngleSlider.Value;
float sweepAngle = (float)sweepAngleSlider.Value;
canvas.DrawOval(rect, outlinePaint);
using (SKPath path = new SKPath())
{
path.AddArc(rect, startAngle, sweepAngle);
canvas.DrawPath(path, arcPaint);
}
}
Como puede ver, tanto el ángulo inicial como el ángulo de barrido pueden asumir valores negativos:
Este método para generar un arco es algorítmicamente el más simple y es fácil derivar las ecuaciones paramétricas que describen el arco. Conocer el tamaño y la ubicación de la elipse, y los ángulos de inicio y barrido, los puntos inicial y final del arco se pueden calcular mediante trigonometría simple:
x = oval.MidX + (oval.Width / 2) * cos(angle)
y = oval.MidY + (oval.Height / 2) * sin(angle)
El valor de angle es startAngle o startAngle + sweepAngle.
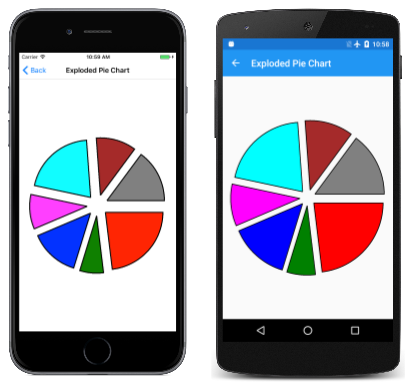
El uso de dos ángulos para definir un arco es el mejor para los casos en los que conoce la longitud angular del arco que desea dibujar, por ejemplo, para crear un gráfico circular. La página del Gráfico circular ampliado lo demuestra. La clase ExplodedPieChartPage usa una clase interna para definir algunos datos y colores fabricados:
class ChartData
{
public ChartData(int value, SKColor color)
{
Value = value;
Color = color;
}
public int Value { private set; get; }
public SKColor Color { private set; get; }
}
ChartData[] chartData =
{
new ChartData(45, SKColors.Red),
new ChartData(13, SKColors.Green),
new ChartData(27, SKColors.Blue),
new ChartData(19, SKColors.Magenta),
new ChartData(40, SKColors.Cyan),
new ChartData(22, SKColors.Brown),
new ChartData(29, SKColors.Gray)
};
El controlador PaintSurface recorre primero los elementos para calcular un número de totalValues. A partir de eso, puede determinar el tamaño de cada elemento como la fracción del total y convertirlo en un ángulo:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
int totalValues = 0;
foreach (ChartData item in chartData)
{
totalValues += item.Value;
}
SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
float explodeOffset = 50;
float radius = Math.Min(info.Width / 2, info.Height / 2) - 2 * explodeOffset;
SKRect rect = new SKRect(center.X - radius, center.Y - radius,
center.X + radius, center.Y + radius);
float startAngle = 0;
foreach (ChartData item in chartData)
{
float sweepAngle = 360f * item.Value / totalValues;
using (SKPath path = new SKPath())
using (SKPaint fillPaint = new SKPaint())
using (SKPaint outlinePaint = new SKPaint())
{
path.MoveTo(center);
path.ArcTo(rect, startAngle, sweepAngle, false);
path.Close();
fillPaint.Style = SKPaintStyle.Fill;
fillPaint.Color = item.Color;
outlinePaint.Style = SKPaintStyle.Stroke;
outlinePaint.StrokeWidth = 5;
outlinePaint.Color = SKColors.Black;
// Calculate "explode" transform
float angle = startAngle + 0.5f * sweepAngle;
float x = explodeOffset * (float)Math.Cos(Math.PI * angle / 180);
float y = explodeOffset * (float)Math.Sin(Math.PI * angle / 180);
canvas.Save();
canvas.Translate(x, y);
// Fill and stroke the path
canvas.DrawPath(path, fillPaint);
canvas.DrawPath(path, outlinePaint);
canvas.Restore();
}
startAngle += sweepAngle;
}
}
Se crea un nuevo objeto SKPath para cada segmento circular. La ruta de acceso consta de una línea desde el centro y, a continuación, un ArcTo para dibujar el arco y otra línea hacia atrás al centro resulta de la llamada Close. Este programa muestra segmentos circulares "explotados" moviéndolos todos fuera del centro en 50 píxeles. Esa tarea requiere un vector en la dirección del punto medio del ángulo de barrido para cada segmento:
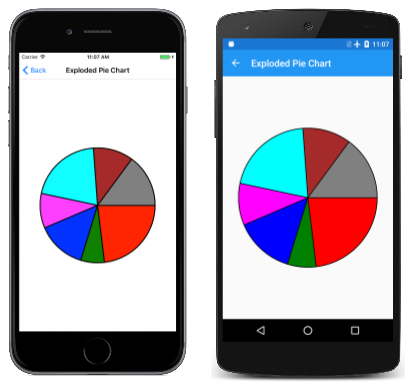
Para ver lo que parece sin la "explosión", simplemente comente la llamada Translate:
El arco tangente
El segundo tipo de arco admitido por SKPath es el arco tangente, denominado porque el arco es la circunferencia de un círculo que es tangente a dos líneas conectadas.
Se agrega un arco tangente a una ruta de acceso con una llamada al método ArcTo con dos parámetros SKPoint o la sobrecarga de ArcTo con parámetros de Single independientes para los puntos:
public void ArcTo (SKPoint point1, SKPoint point2, Single radius)
public void ArcTo (Single x1, Single y1, Single x2, Single y2, Single radius)
Este método ArcTo es similar a la función PostScript arct (página 532) y al método AddArcToPoint de iOS.
El método ArcTo implica tres puntos:
- El punto actual del contorno o el punto (0, 0) si no se ha llamado a
MoveTo - El primer argumento de punto para el método
ArcTo, denominado punto de esquina - El segundo argumento de punto para
ArcTo, denominado punto de destino:

Estos tres puntos definen dos líneas conectadas:
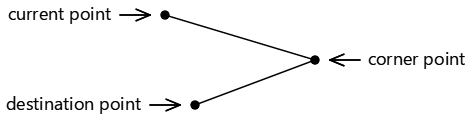
Si los tres puntos son colineales, es decir, si se encuentran en la misma línea recta, no se dibujará ningún arco.
El método ArcTo también incluye un parámetro radius. Esto define el radio de un círculo:

El arco tangente no se generaliza para una elipse.
Si las dos líneas se encuentran en cualquier ángulo, ese círculo se puede insertar entre esas líneas para que sea tangente a ambas líneas:
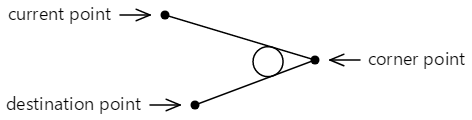
La curva que se agrega al contorno no toca ninguno de los puntos especificados en el método ArcTo. Consta de una línea recta desde el punto actual hasta el primer punto tangente, y un arco que termina en el segundo punto tangente, que se muestra aquí en rojo:
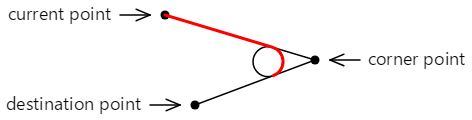
Esta es la línea recta final y el arco que se agrega al contorno:

El contorno puede continuar desde el segundo punto tangente.
La página Arco tangente le permite experimentar con el arco tangente. Esta es la primera de varias páginas que derivan de InteractivePage, que define algunos objetos SKPaint útiles y realiza TouchPoint procesamiento:
public class InteractivePage : ContentPage
{
protected SKCanvasView baseCanvasView;
protected TouchPoint[] touchPoints;
protected SKPaint strokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
StrokeWidth = 3
};
protected SKPaint redStrokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Red,
StrokeWidth = 15
};
protected SKPaint dottedStrokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
StrokeWidth = 3,
PathEffect = SKPathEffect.CreateDash(new float[] { 7, 7 }, 0)
};
protected void OnTouchEffectAction(object sender, TouchActionEventArgs args)
{
bool touchPointMoved = false;
foreach (TouchPoint touchPoint in touchPoints)
{
float scale = baseCanvasView.CanvasSize.Width / (float)baseCanvasView.Width;
SKPoint point = new SKPoint(scale * (float)args.Location.X,
scale * (float)args.Location.Y);
touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
}
if (touchPointMoved)
{
baseCanvasView.InvalidateSurface();
}
}
}
La clase TangentArcPage deriva de InteractivePage. El constructor del archivo TangentArcPage.xaml.cs es responsable de crear instancias e inicializar la matriz touchPoints y establecer baseCanvasView (en InteractivePage) en el objeto SKCanvasView creado en la instancia del archivo TangentArcPage.xaml:
public partial class TangentArcPage : InteractivePage
{
public TangentArcPage()
{
touchPoints = new TouchPoint[3];
for (int i = 0; i < 3; i++)
{
TouchPoint touchPoint = new TouchPoint
{
Center = new SKPoint(i == 0 ? 100 : 500,
i != 2 ? 100 : 500)
};
touchPoints[i] = touchPoint;
}
InitializeComponent();
baseCanvasView = canvasView;
radiusSlider.Value = 100;
}
void sliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
...
}
El controlador PaintSurface usa el método ArcTo para dibujar el arco en función de los puntos táctiles y un Slider, pero también calcula de forma algorítmica el círculo en el que se basa el ángulo:
public partial class TangentArcPage : InteractivePage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw the two lines that meet at an angle
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.LineTo(touchPoints[1].Center);
path.LineTo(touchPoints[2].Center);
canvas.DrawPath(path, dottedStrokePaint);
}
// Draw the circle that the arc wraps around
float radius = (float)radiusSlider.Value;
SKPoint v1 = Normalize(touchPoints[0].Center - touchPoints[1].Center);
SKPoint v2 = Normalize(touchPoints[2].Center - touchPoints[1].Center);
double dotProduct = v1.X * v2.X + v1.Y * v2.Y;
double angleBetween = Math.Acos(dotProduct);
float hypotenuse = radius / (float)Math.Sin(angleBetween / 2);
SKPoint vMid = Normalize(new SKPoint((v1.X + v2.X) / 2, (v1.Y + v2.Y) / 2));
SKPoint center = new SKPoint(touchPoints[1].Center.X + vMid.X * hypotenuse,
touchPoints[1].Center.Y + vMid.Y * hypotenuse);
canvas.DrawCircle(center.X, center.Y, radius, this.strokePaint);
// Draw the tangent arc
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.ArcTo(touchPoints[1].Center, touchPoints[2].Center, radius);
canvas.DrawPath(path, redStrokePaint);
}
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
// Vector methods
SKPoint Normalize(SKPoint v)
{
float magnitude = Magnitude(v);
return new SKPoint(v.X / magnitude, v.Y / magnitude);
}
float Magnitude(SKPoint v)
{
return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
}
}
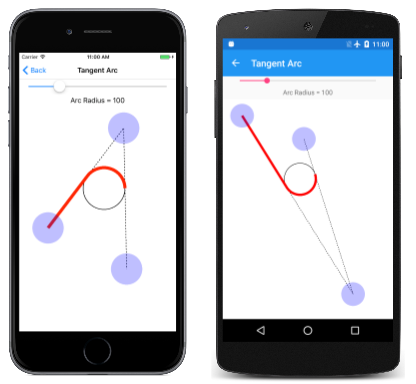
Esta es la página de Arco tangente que se ejecuta:
El arco tangente es ideal para crear esquinas redondeadas, como un rectángulo redondeado. Dado que SKPath ya incluye un método AddRoundedRect, la página Heptágono redondeado muestra cómo usar ArcTo para redondear las esquinas de un polígono de siete lados. (El código se generaliza para cualquier polígono normal).
El controlador PaintSurface de la clase RoundedHeptagonPage contiene un bucle for para calcular las coordenadas de los siete vértices del heptágono y un segundo para calcular los puntos intermedios de los siete lados de estos vértices. A continuación, estos puntos intermedios se usan para construir la ruta de acceso:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
float cornerRadius = 100;
int numVertices = 7;
float radius = 0.45f * Math.Min(info.Width, info.Height);
SKPoint[] vertices = new SKPoint[numVertices];
SKPoint[] midPoints = new SKPoint[numVertices];
double vertexAngle = -0.5f * Math.PI; // straight up
// Coordinates of the vertices of the polygon
for (int vertex = 0; vertex < numVertices; vertex++)
{
vertices[vertex] = new SKPoint(radius * (float)Math.Cos(vertexAngle),
radius * (float)Math.Sin(vertexAngle));
vertexAngle += 2 * Math.PI / numVertices;
}
// Coordinates of the midpoints of the sides connecting the vertices
for (int vertex = 0; vertex < numVertices; vertex++)
{
int prevVertex = (vertex + numVertices - 1) % numVertices;
midPoints[vertex] = new SKPoint((vertices[prevVertex].X + vertices[vertex].X) / 2,
(vertices[prevVertex].Y + vertices[vertex].Y) / 2);
}
// Create the path
using (SKPath path = new SKPath())
{
// Begin at the first midpoint
path.MoveTo(midPoints[0]);
for (int vertex = 0; vertex < numVertices; vertex++)
{
SKPoint nextMidPoint = midPoints[(vertex + 1) % numVertices];
// Draws a line from the current point, and then the arc
path.ArcTo(vertices[vertex], nextMidPoint, cornerRadius);
// Connect the arc with the next midpoint
path.LineTo(nextMidPoint);
}
path.Close();
// Render the path in the center of the screen
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Blue;
paint.StrokeWidth = 10;
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.DrawPath(path, paint);
}
}
}
Esta es la ejecución del programa:
El arco elíptico
El arco elíptico se agrega a una ruta de acceso con una llamada al método ArcTo que tiene dos parámetros SKPoint o la sobrecarga de ArcTo con coordenadas X e Y independientes:
public void ArcTo (SKPoint r, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, SKPoint xy)
public void ArcTo (Single rx, Single ry, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, Single x, Single y)
El arco elíptico es coherente con el arco elíptico incluido en los gráficos vectoriales escalables (SVG) y la clase ArcSegment de la Plataforma universal de Windows.
Estos métodos ArcTo dibujan un arco entre dos puntos, que son el punto actual del contorno, y el último parámetro al método ArcTo (el parámetro xy o los parámetros x y y independientes):

El primer parámetro de punto para el método ArcTo (r, o rx y ry) no es un punto en absoluto, sino que especifica los radios horizontales y verticales de una elipse;
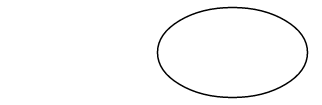
El parámetro xAxisRotate es el número de grados en sentido de las agujas del reloj para girar esta elipse:

Si esta elipse inclinada se coloca para que toque los dos puntos, los puntos están conectados por dos arcos diferentes:
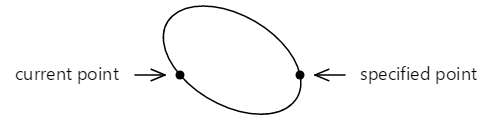
Estos dos arcos se pueden distinguir de dos maneras: el arco superior es mayor que el arco inferior y, a medida que el arco se dibuja de izquierda a derecha, el arco superior se dibuja en una dirección en sentido de las agujas del reloj mientras que el arco inferior se dibuja en una dirección en sentido contrario a las agujas del reloj.
También es posible ajustar la elipse entre los dos puntos de otra manera:
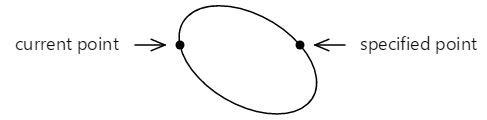
Ahora hay un arco más pequeño en la parte superior que se dibuja en el sentido de las agujas del reloj y un arco más grande en la parte inferior que se dibuja en sentido contrario a las agujas del reloj.
Por lo tanto, estos dos puntos se pueden conectar mediante un arco definido por la elipse inclinada en un total de cuatro maneras:

Estos cuatro arcos se distinguen por las cuatro combinaciones de los argumentos de tipo de enumeración SKPathArcSize y SKPathDirection para el método ArcTo:
- rojo: SKPathArcSize.Large y SKPathDirection.Clockwise
- verde: SKPathArcSize.Small y SKPathDirection.Clockwise
- blue: SKPathArcSize.Small y SKPathDirection.CounterClockwise
- magenta: SKPathArcSize.Large y SKPathDirection.CounterClockwise
Si la elipse inclinada no es lo suficientemente grande como para caber entre los dos puntos, se escala uniformemente hasta que es lo suficientemente grande. Solo dos arcos únicos conectan los dos puntos en ese caso. Se pueden distinguir con el parámetro SKPathDirection.
Aunque este enfoque para definir un arco suena complejo en primer lugar, es el único enfoque que permite definir un arco con una elipse girada, y a menudo es el enfoque más sencillo cuando se necesitan integrar arcos con otras partes del contorno.
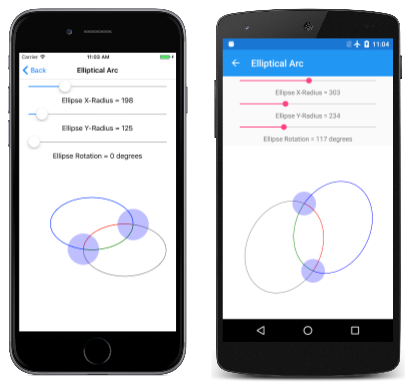
La página Arco elíptico permite establecer interactivamente los dos puntos y el tamaño y la rotación de la elipse. La clase EllipticalArcPage deriva de InteractivePage y el controlador PaintSurface del archivo de código subyacente EllipticalArcPage.xaml.cs dibuja los cuatro arcos:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPath path = new SKPath())
{
int colorIndex = 0;
SKPoint ellipseSize = new SKPoint((float)xRadiusSlider.Value,
(float)yRadiusSlider.Value);
float rotation = (float)rotationSlider.Value;
foreach (SKPathArcSize arcSize in Enum.GetValues(typeof(SKPathArcSize)))
foreach (SKPathDirection direction in Enum.GetValues(typeof(SKPathDirection)))
{
path.MoveTo(touchPoints[0].Center);
path.ArcTo(ellipseSize, rotation,
arcSize, direction,
touchPoints[1].Center);
strokePaint.Color = colors[colorIndex++];
canvas.DrawPath(path, strokePaint);
path.Reset();
}
}
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
Aquí se está ejecutando:
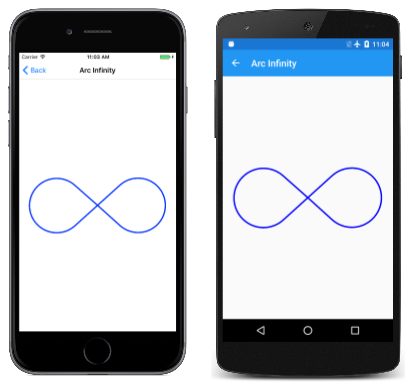
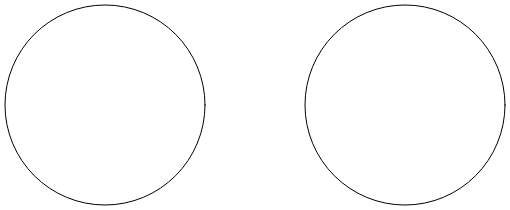
La página Arc infinito usa el arco elíptico para dibujar un signo infinito. El signo infinito se basa en dos círculos con radios de 100 unidades separadas por 100 unidades:
Dos líneas cruzando entre sí son tangentes a ambos círculos:
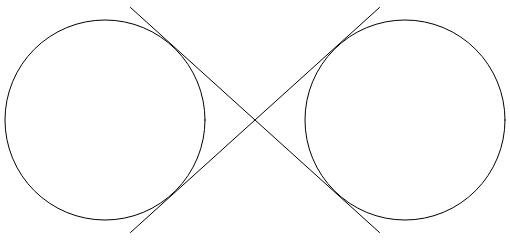
El signo infinito es una combinación de partes de estos círculos y las dos líneas. Para usar el arco elíptico para dibujar el signo infinito, se deben determinar las coordenadas en las que las dos líneas son tangentes a los círculos.
Construya un rectángulo derecho en uno de los círculos:
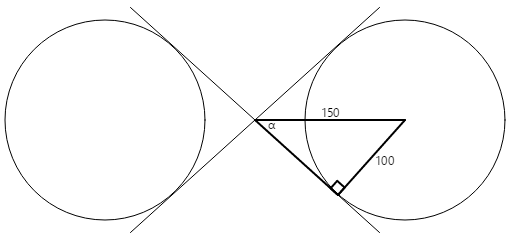
El radio del círculo es de 100 unidades y la hipotenusa del triángulo es de 150 unidades, por lo que el ángulo α es el arcoseno (seno inverso) de 100 dividido entre 150 o 41,8 grados. La longitud del otro lado del triángulo es 150 veces el coseno de 41,8 grados, o 112, que también se puede calcular mediante el Teorema de Pitágoras.
Las coordenadas del punto tangente se pueden calcular mediante esta información:
x = 112·cos(41.8) = 83
y = 112·sin(41.8) = 75
Los cuatro puntos tangentes son todos los necesarios para dibujar un signo infinito centrado en el punto (0, 0) con radios de círculo de 100:
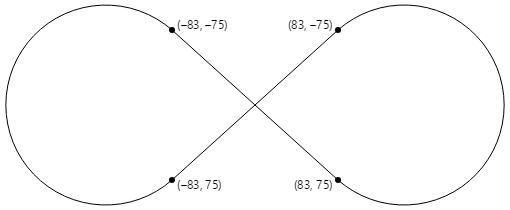
El controlador PaintSurface de la clase ArcInfinityPage coloca el signo infinito para que el punto (0, 0) se coloque en el centro de la página y escale la ruta de acceso al tamaño de pantalla:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPath path = new SKPath())
{
path.LineTo(83, 75);
path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.CounterClockwise, 83, -75);
path.LineTo(-83, 75);
path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.Clockwise, -83, -75);
path.Close();
// Use path.TightBounds for coordinates without control points
SKRect pathBounds = path.Bounds;
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(Math.Min(info.Width / pathBounds.Width,
info.Height / pathBounds.Height));
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Blue;
paint.StrokeWidth = 5;
canvas.DrawPath(path, paint);
}
}
}
El código usa la propiedad Bounds de SKPath para determinar las dimensiones del seno infinito para escalarla al tamaño del lienzo:
El resultado parece un poco pequeño, lo que sugiere que la propiedad Bounds de SKPath informa de un tamaño mayor que la ruta de acceso.
Internamente, Skia aproxima el arco utilizando múltiples curvas cuadráticas de Bézier. Estas curvas (como verá en la sección siguiente) contienen puntos de control que rigen cómo se dibuja la curva, pero no forman parte de la curva representada. La propiedad Bounds incluye esos puntos de control.
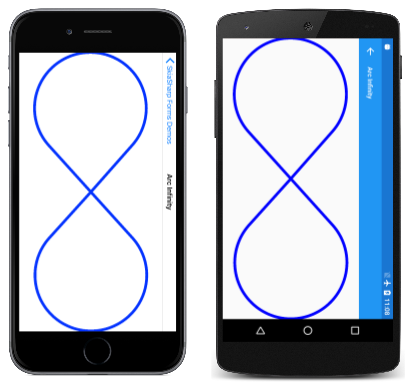
Para obtener un ajuste más ajustado, use la propiedad TightBounds, que excluye los puntos de control. Este es el programa que se ejecuta en modo horizontal y usa la propiedad TightBounds para obtener los límites de ruta de acceso:
Aunque las conexiones entre los arcos y las líneas rectas son matemáticamente suaves, el cambio de arco a línea recta podría parecer un poco abrupto. Se presenta un signo infinito mejor en el siguiente artículo sobre Tres tipos de curvas Bézier.