3.1.8.1.4 DWT
Each tile component (Y, Cb, Cr) is individually transformed by a 2-D DWT using a 5/3 wavelet basis. The filter coefficients used for both of the lifting-based implementations are presented in the following figure.
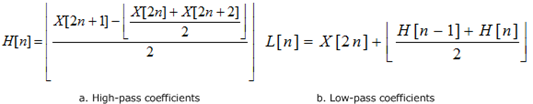
Figure 6: Lifting equations for the DWT
Filtering at the boundary is done by mirroring the input coefficients. For example, if there are eight input coefficients:
-
[0, 1, 2, 3, 4, 5, 6, 7]
then, after mirroring, the coefficients get logically extended as follows:
-
[…, 7, 6, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, 6, 7, 6, 5, 4, 3, 2, 1, 0, …]
Use this logical extension when filtering at boundaries where coefficients are required before or after the first and last available coefficient.
For each level of decomposition, we first perform the DWT in the vertical direction, followed by the DWT in the horizontal direction. After the first level of decomposition, there are 4 sub-bands: LL1, LH1, HL1, HH1. For each successive level of decomposition, the LL sub-band of the previous level is used as the input. Each tile component undergoes three levels of decomposition. This results in 10 sub-bands per component. LH1, HL1, and HH1 contain the highest frequency bands present in the image tile, while LL3 contains the lowest frequency band.
The three-level DWT decomposition is illustrated in the following figure.
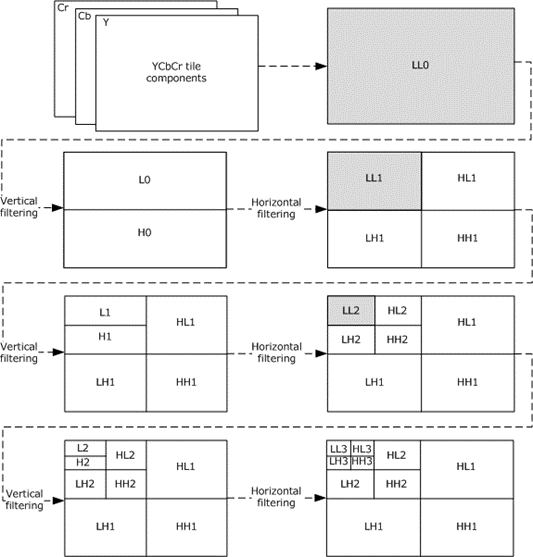
Figure 7: Three-level DWT decomposition