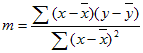Método WorksheetFunction.LinEst (Excel)
Calcula las estadísticas de una línea mediante el método de mínimos cuadrados para calcular una línea recta que mejor se adapte a los datos y devuelve una matriz que describe la línea. Como esta función devuelve una matriz de valores, debe especificarse como una fórmula de matriz.
Sintaxis
expresión. LinEst (Arg1, Arg2, Arg3, Arg4)
Expresión Variable que representa un objeto WorksheetFunction .
Parameters
| Nombre | Obligatorio/opcional | Tipo de datos | Descripción |
|---|---|---|---|
| Arg1 | Obligatorio | Variant | Known_y: el conjunto de valores y que ya conoce en la relación y = mx + b. |
| Arg2 | Opcional | Variant | Valores conocidos de x: conjunto opcional de valores de x que se conocen en la relación y = mx+b. |
| Arg3 | Opcional | Variant | Constante: un valor lógico que especifica si se fuerza la constante b para que sea igual a 0. |
| Arg4 | Opcional | Variant | Estadística: valor lógico que especifica si se van a devolver estadísticas de regresión adicionales. |
Valor devuelto
Variant
Comentarios
La ecuación de la línea es y = mx + b o y = m1x1 + m2x2 + ... + b (si hay varios intervalos de valores x), donde el valor y dependiente es una función de los valores x independientes. Los valores de m son coeficientes que corresponden a cada valor de x y b es un valor constante. Tenga en cuenta que y, x y m pueden ser vectores. La matriz que LinEst devuelve es {mn,mn-1,...,m1,b}. LinEst también puede devolver estadísticas de regresión adicionales.
Si la matriz known_y está en una sola columna, cada columna de known_x se interpreta como una variable independiente.
Si la matriz known_y está en una sola fila, cada fila de known_x se interpreta como una variable independiente.
La matriz de valores conocidos de x puede incluir uno o varios conjuntos de variables. Si solo se usa una variable, los valores conocidos de y y de x pueden ser rangos de cualquier forma, siempre y cuando tengan las mismas dimensiones. Si se usa más de una variable, los valores conocidos de y deben ser un vector (es decir, un rango con un alto de una fila o un ancho de una columna).
Si se omite el de known_x, se supone que es la matriz {1,2,3,...} que tiene el mismo tamaño que known_y.
Si const es True o se omite, b se calcula normalmente.
Si const es False, b se establece en 0 y los valores m se ajustan para ajustarse
y = mxa .Si stats es True, LinEst devuelve las estadísticas de regresión adicionales, por lo que la matriz devuelta es
{mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}.Si stats es False o se omite, LinEst devuelve solo los coeficientes m y la constante b.
Las estadísticas de regresión adicionales son las siguientes:
| Estadística de regresión | Descripción |
|---|---|
| se1,se2,...,sen | Valores de error típicos para los coeficientes m1,m2,...,mn. |
| Seb | Valor de error estándar de la constante b (seb = #N/A cuando const es False). |
| R2 | Coeficiente de determinación. Compara los valores de y previstos y reales y asigna un valor de 0 a 1. Si es 1, hay una correlación perfecta en el ejemplo: no hay ninguna diferencia entre el valor y estimado y el valor y real. En el otro extremo, si el coeficiente de determinación es 0, la ecuación de regresión no sirve para predecir el valor de y. |
| Sey | Error típico para el valor previsto de y. |
| F | La estadística F o el valor observado por F. Use la estadística F para determinar si la relación observada entre las variables dependientes e independientes se produce por casualidad. |
| Df | Grados de libertad. Utilice los grados de libertad para hallar valores críticos de F en una tabla estadística. Compare los valores que encuentra en la tabla con la estadística F devuelta por LinEst para determinar un nivel de confianza para el modelo. |
| ssreg | Suma de regresión de cuadrados. |
| ssresid | Suma residual de cuadrados. |
En la siguiente ilustración se muestra el orden en que se devuelven las estadísticas de regresión adicionales.
Puede describir cualquier línea recta con la pendiente y la intersección Y: Slope (m). Para encontrar la pendiente de una línea, a menudo escrita como m, tome dos puntos en la línea, (x1,y1) y (x2,y2); la pendiente es igual a (y2 - y1)/(x2 - x1). Y-intercept (b): la intersección y de una línea, a menudo escrita como b, es el valor de y en el punto donde la línea cruza el eje Y. La ecuación de una línea recta es y = mx + b. Después de conocer los valores de m y b, puede calcular cualquier punto de la línea conectando el valor y o x a esa ecuación. Se puede utilizar también la función TREND.
Cuando solo tiene una variable x independiente, puede obtener los valores de pendiente e intersección Y directamente mediante las fórmulas siguientes:
- Pendiente:
=INDEX(LINEST(known_y's,known_x's),1) - Interceptación Y:
=INDEX(LINEST(known_y's,known_x's),2)
La precisión de la línea calculada por LinEst depende del grado de dispersión de los datos. Cuantos más lineales sean los datos, más preciso será el modelo LinEst . LinEst usa el método de mínimos cuadrados para determinar el mejor ajuste para los datos. Cuando solo tiene una variable x independiente, los cálculos de m y b se basan en las fórmulas siguientes:
donde x e y son medios de ejemplo, es decir, x = AVERAGE (x conocidos) e y = AVERAGE(known_y).
Las funciones de ajuste de línea y curva LinEst y LogEst pueden calcular la mejor línea recta o curva exponencial que se adapte a los datos. Sin embargo, tendrá que decidir cuál de los dos resultados se adapta mejor a los datos. Puede calcular TREND(known_y's,known_x's) para una línea recta o GROWTH(known_y's, known_x's) para una curva exponencial. Estas funciones, sin el argumento de valores nuevos de x, devuelven una matriz de valores y previstos a lo largo de la línea o curva en los puntos de datos reales. A continuación, puede comparar los valores previstos con los valores reales. Puede ser conveniente dibujarlos en un gráfico para poder compararlos visualmente.
En el análisis de regresión, Microsoft Excel calcula para cada punto la diferencia al cuadrado entre el valor y estimado para ese punto y su valor y real. La suma de estas diferencias al cuadrado se denomina suma residual de los cuadrados, ssresid. A continuación, Excel calcula la suma total de cuadrados, sstotal. Cuando el valor constante es TRUE o se omite, la suma total de los cuadrados es la suma de las diferencias al cuadrado entre los valores de y reales y la media de los valores de y. Cuando el valor constante es FALSE, la suma total de los cuadrados es la suma de los cuadrados de los valores de y reales (sin restar el valor medio de y de cada valor de y). A continuación, se puede encontrar la suma de regresión de cuadrados, ssreg, en ssreg = sstotal - ssresid. Cuanto menor sea la suma residual de cuadrados, en comparación con la suma total de cuadrados, mayor será el valor del coeficiente de determinación, r2, que es un indicador del grado en que la ecuación resultante del análisis de regresión explica la relación entre las variables; r2 es igual a ssreg/sstotal.
En algunos casos, una o varias de las columnas X (supongamos que Y y X están en columnas) pueden no tener ningún valor predictivo adicional en presencia de las otras columnas X. En otras palabras, la eliminación de una o varias columnas X podría dar lugar a valores Y predichos que sean igualmente precisos. En ese caso, estas columnas X redundantes deben omitirse del modelo de regresión. Este fenómeno se denomina colinearidad porque cualquier columna X redundante se puede expresar como una suma de múltiplos de las columnas X no redundantes. LinEst comprueba si hay colinearidad y quita las columnas X redundantes del modelo de regresión cuando las identifica. Las columnas X eliminadas se pueden reconocer en la salida LinEst como que tienen 0 coeficientes, así como 0 se.
- Si una o varias columnas se quitan como redundantes, df se ve afectado porque df depende del número de columnas X que se usan realmente con fines predictivos. Si df se cambia porque se quitan las columnas X redundantes, los valores de sey y F también se ven afectados.
- La colinearidad debe ser relativamente rara en la práctica. Sin embargo, un caso en el que es más probable que surja es cuando algunas columnas X contienen solo 0 y 1 como indicadores de si un sujeto de un experimento es o no miembro de un grupo determinado. Si const = TRUE o se omite, LinEst inserta eficazmente una columna X adicional de los 1 para modelar la interceptación. Si tiene una columna con un 1 para cada sujeto si es varón, o 0 si no, y también tiene una columna con un 1 para cada sujeto si es mujer, o 0 si no, esta última columna es redundante porque las entradas en ella se pueden obtener de restar la entrada en la columna de indicador masculino de la entrada en la columna adicional de los 1 agregados por LinEst.
- df se calcula de la siguiente manera cuando no se quita ninguna columna X del modelo debido a la colinearidad: si hay k columnas de known_x y const = TRUE o omitidas,
df = n - k - 1. Si const = FALSE,df = n - k. En ambos casos, cada columna X se quita debido a que la colinealidad aumenta en 1 el valor de df.
Las fórmulas que devuelven matrices deben escribirse como fórmulas de matriz.
- Cuando especifique como argumento una constante matricial, como valores conocidos de x, utilice comas para separar los valores de una misma fila y signos de punto y coma para separar las filas. Los caracteres separadores pueden ser diferentes según la configuración local definida en Configuración regional y de idioma en el Panel de control.
- Tenga en cuenta que los valores de y previstos por la ecuación de regresión puede que no sean válidos si quedan fuera del rango de los valores de y utilizados para determinar la ecuación.
El algoritmo subyacente usado en la función LinEst es diferente del algoritmo subyacente usado en las funciones Slope e Intercept . La diferencia entre estos algoritmos puede producir resultados distintos cuando los datos son indeterminados y colineales. Por ejemplo, si los puntos de datos del argumento de valores conocidos de y son 0 y los puntos de datos del argumento de valores conocidos de x son 1:
- LinEst devuelve un valor de 0. El algoritmo LinEst está diseñado para devolver resultados razonables para los datos collinear y, en este caso, se puede encontrar al menos una respuesta.
- Pendiente e interceptación devuelven un #DIV/0! Error. El algoritmo Slope e Intercept está diseñado para buscar una respuesta y, en este caso, puede haber más de una respuesta.
Soporte técnico y comentarios
¿Tiene preguntas o comentarios sobre VBA para Office o esta documentación? Vea Soporte técnico y comentarios sobre VBA para Office para obtener ayuda sobre las formas en las que puede recibir soporte técnico y enviar comentarios.