Resultados de los modelos de aprendizaje automático
Este artículo analiza las matrices de confusión, los problemas de clasificación y la precisión en los modelos de aprendizaje automático (ML). El propósito es mejorar su conocimiento de la precisión en los resultados de la predicción de ML. El público objetivo incluye ingenieros, analistas y gerentes que desean desarrollar sus conocimientos y habilidades en ciencia de datos.
Matriz de confusión
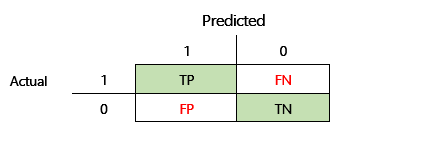
Una vez que se entrena un problema de ML supervisado en un conjunto de datos históricos, se prueba mediante el uso de datos que se retienen del proceso de entrenamiento. De esta forma, puede comparar las predicciones del modelo entrenado con los valores reales. La matriz de confusión proporciona un medio para evaluar el éxito de un problema de clasificación y dónde se cometen errores (es decir, dónde se vuelve "confuso").
Por ejemplo, su objetivo es predecir si una mascota es un perro o un gato, basándose en algunos atributos físicos y de comportamiento. Si tiene un conjunto de datos de prueba que contiene 30 perros y 20 gatos, la matriz de confusión puede parecerse a la siguiente ilustración.
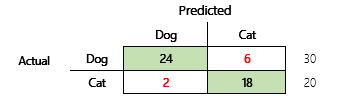
Los números de las celdas verdes representan predicciones correctas. Como puede ver, el modelo predijo correctamente un porcentaje más alto de gatos reales. La precisión general del modelo es fácil de calcular. En este caso, es 42 ÷ 50, o sea 0,84.
Clasificadores de clases múltiples en una matriz de confusión
La mayoría de las discusiones sobre la matriz de confusión se centran en clasificadores binarios, como en el ejemplo anterior. Este caso es un caso especial en el que se pueden considerar otras métricas, como la sensibilidad y la recuperación.
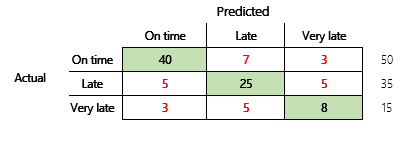
A continuación, consideraremos un problema de clasificación para un escenario financiero que tiene tres estados. El modelo predice si la factura de un cliente se pagará a tiempo, tarde o muy tarde. Por ejemplo, de 100 facturas de prueba, 50 se pagan a tiempo, 35 se pagan con retraso y 15 se pagan con mucho retraso. En este caso, un modelo puede producir una matriz de confusión similar a la siguiente ilustración.
 ]
]
Una matriz de confusión proporciona mucha más información que una simple métrica de precisión. Sin embargo, pese a ello es relativamente fácil de entender. Una matriz de confusión le dice si tiene un conjunto de datos equilibrado donde las clases de salida tienen recuentos similares. Para el escenario de clases múltiples, le indica lo desacertada que podría ser una predicción cuando las clases de salida son ordinales, como en el ejemplo anterior sobre pagos de clientes.
Precisión del modelo
Las diferentes métricas de precisión tienen la ventaja de cuantificar la calidad del modelo.
Debido a que la precisión es una métrica fácil de entender, es un buen punto de partida para explicar un modelo a otras personas, especialmente a los usuarios del modelo que no son científicos de datos. No se requieren conocimientos de estadística para comprender la precisión del modelo. Cuando se dispone de una matriz de confusión, proporciona más información sobre el rendimiento del modelo.
Sin embargo, para una comprensión más profunda, deben tenerse en cuenta varios desafíos asociados con la precisión. La utilidad de la métrica depende del contexto del problema. Una pregunta que surge a menudo en relación con el rendimiento del modelo es: "¿Qué tan bueno es el modelo?" Sin embargo, la respuesta a esta pregunta no es necesariamente sencilla. Considere la siguiente matriz de confusión (modelo 2).
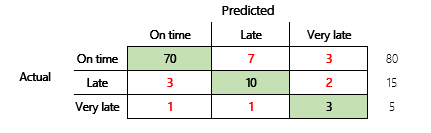
Un cálculo rápido muestra que la precisión de este modelo es (70 + 10 + 3) ÷ 100, o sea 0,83. En la superficie, este resultado parece mejor que el resultado del modelo multiclase anterior (modelo 1), que tiene una precisión de 0,73. ¿Pero es mejor?
Para comenzar a abordar esta pregunta, considere la precisión de una suposición ingenua. Para un problema de clasificación, una simple suposición siempre predecirá la clase más común. Para el modelo 1, esa suposición será "en el momento" y producirá una precisión de 0,50. La suposición para el modelo 2 será también "en el momento" y producirá una precisión de 0,80. Debido a que el modelo 1 mejora la suposición ingenua en 0,73 - 0,50 = 0,23, mientras que el modelo 2 mejora la suposición ingenua en 0,83 - 0,80 = 0,03, el modelo 1 es un modelo mejor, aunque tiene una precisión menor. El cálculo revela que la evaluación eficaz de la calidad de un modelo requiere más contexto que el valor de la precisión.
Otro aspecto que cabe destacar. Considere un escenario en el que se utiliza una prueba médica para detectar una enfermedad en un paciente. Este problema es un problema de clasificación binaria donde un resultado positivo indica que el paciente tiene la enfermedad. En este escenario, debe pensar en el impacto de los siguientes errores:
- Falsos positivos, donde la prueba dice que una paciente tiene la enfermedad, pero en realidad no la tiene.
- Falsos negativos, donde la prueba dice que una paciente no tiene la enfermedad, pero en realidad la tiene.
Obviamente, ambos tipos de error son indeseables, pero ¿cuál es peor? De nuevo, depende. En el caso de una enfermedad potencialmente mortal que requiere un tratamiento rápido, la minimización de los falsos negativos (con suerte, seguida de pruebas adicionales) tiene prioridad. En otras situaciones menos críticas, los creadores del modelo pueden minimizar los falsos positivos. En cualquier caso, una conclusión razonable es que, para determinar de forma eficaz la calidad de un modelo, debe tener más información de la que proporciona una métrica de precisión.
Recomendaciones
La precisión es una herramienta importante para comunicarse con expertos en el dominio que no están familiarizados con las estadísticas. Sin embargo, para que la información sea útil, es fundamental que se proporcione un contexto adicional junto con el valor de precisión.
Para el escenario de predicción de pagos, puede establecer un objetivo para el modelo de ML que incluya factores en diferentes comportamientos de pago. El objetivo es que el modelo mejore una suposición ingenua al reducir el número de respuestas incorrectas en al menos un 50 por ciento. En otras palabras, desea una precisión objetivo que divida la diferencia entre la precisión de una suposición ingenua y el 100 por ciento.
La siguiente tabla resume este principio para las matrices de confusión en este artículo.
| Modelo | Suposición ingenua | Destino | Precisión del modelo | ¿Se alcanzó el objetivo? |
|---|---|---|---|---|
| Modelo 1 | 0.50 | 0.75 | 0.73 | Casi. Este modelo mejora significativamente la suposición. |
| Modelo 2 | 0.80 | 0.90 | 0.83 | Nº Se requiere una mejora. |
Precisión de clasificación F1
La consideración final en este artículo es una medida más avanzada del rendimiento de clasificación ML, que se conoce como precisión F1.
Antes de poder definir la precisión F1, se deben introducir dos métricas adicionales: precisión y recuperación. La precisión indica cuántas del número total de predicciones que se especifican como positivas se asignaron correctamente. Esta métrica también se conoce como valor predictivo positivo. Recuperación es el número total de casos positivos reales que se predijeron correctamente. Esta métrica también se conoce como sensibilidad.
En la matriz de confusión de la ilustración anterior, estas métricas se calculan de la siguiente manera:
- Precisión = TP ÷ (TP + FP)
- Recuperación = TP ÷ (TP + FN)
La medida F1 combina precisión y recuperación. El resultado es la media armónica de los dos valores. Se calcula de la siguiente manera:
- F1 = 2 × (Precisión × Recuperación) ÷ (Precisión + Recuperación)
Veamos un ejemplo concreto. Anteriormente en este artículo, hubo un ejemplo de un modelo que predijo si un animal era un perro o un gato. Aquí se repite la ilustración.
Estos son los resultados si se utiliza "Perro" como respuesta positiva.
- Precisión = 24 ÷ (24 + 2) = 0,9231
- Recuperación = 24 ÷ (24 + 6) = 0,8
- F1 = 2 × (0,9231 × 0,8) ÷ (0,9231 + 0,8) = 0,8572
Como puede ver, el valor F1 está entre los valores de precisión y recuperación.
Aunque la precisión de F1 no es tan fácil de entender, agrega matices al número de precisión básico. También puede ayudar con conjuntos de datos no equilibrados, como se mostrará en la siguiente discusión.
La sección Precisión del modelo de este artículo comparó las siguientes dos matrices de confusión. Aunque el primer modelo tenía una precisión menor, se consideró un modelo más útil porque mostró más mejoras que la suposición predeterminada de un pago puntual.


Veamos cómo se comparan estos dos modelos cuando se usa la puntuación F1. La puntuación F1 tiene en cuenta la precisión y la recuperación de cada estado, y el cálculo macro F1 luego promedia la puntuación F1 en todos los estados para determinar una puntuación F1 general. Hay otras variantes de F1, pero es de mayor interés considerar la versión macro, dada la misma consideración que se le da a los tres estados.
Para simplificar los cálculos, se crearon matrices de ejemplo para comparar los valores reales y previstos. Estas matrices utilizaron la biblioteca de métricas de sklearn en Python para calcular los valores. Este es el resultado.
| Modelo | Suposición ingenua | Precisión | Macro F1 |
|---|---|---|---|
| Modelo 1 | 0.5 | 0.73 | 0.67 |
| Modelo 2 | 0.80 | 0.83 | 0.66 |
Para obtener más detalles sobre cómo funciona este cálculo, aquí está el informe de clasificación sklearn.metrics para el modelo 1. Los tres estados, "Puntual", "Tarde" y "Muy tarde", están representados por las filas etiquetadas como 1, 2 y 3, respectivamente. El promedio macro es simplemente el promedio de la columna "f1-score".
| precisión | recuperación | f1-score | |
|---|---|---|---|
| 1 | 0.83 | 0.80 | 0.82 |
| 2 | 0.68 | 0.71 | 0.69 |
| 3 | 0.50 | 0.50 | 0.50 |
Como muestran estos resultados, los dos modelos tienen puntuaciones de precisión macro F1 casi idénticas. En este y muchos otros casos, la precisión F1 proporciona un mejor indicador de la capacidad de un modelo. En cuanto a la precisión, la interpretación de los resultados requiere que comprenda qué es lo más importante a considerar en el modelo.