Clase System.Drawing.Drawing2D.Matrix
En este artículo se proporcionan comentarios adicionales a la documentación de referencia de esta API.
La Matrix clase encapsula una matriz afín de 3 a 3 que representa una transformación geométrica.
En GDI+, puede almacenar una transformación affine en un Matrix objeto . Dado que la tercera columna de una matriz que representa una transformación afín siempre es (0, 0, 1), solo se especifican los seis números de las dos primeras columnas al construir un objeto Matrix. La instrucción Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) construye la matriz que se muestra en la ilustración siguiente.
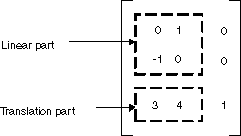
Nota:
En .NET 6 y versiones posteriores, el paquete System.Drawing.Common, que incluye este tipo, solo se admite en sistemas operativos Windows. El uso de este tipo en aplicaciones multiplataforma provoca advertencias en tiempo de compilación y excepciones en tiempo de ejecución. Para obtener más información, consulte System.Drawing.Common only supported on Windows (Solo se admite System.Drawing.Common en Windows).
Transformaciones compuestas
Una transformación compuesta es una secuencia de transformaciones, una seguida de la otra. Tenga en cuenta las matrices y las transformaciones en la lista siguiente:
| Matriz | Transformación |
|---|---|
| Matrix A | Girar 90 grados |
| Matrix B | Escalado por un factor de 2 en la dirección x |
| Matrix C | Trasladar 3 unidades en la dirección y |
Si comienza con el punto (2, 1) - representado por la matriz [2 1 1] y multiplicado por A, después B, C, el punto (2, 1) se somete a las tres transformaciones en el orden enumerado.
[2 1 1]ABC = [-2 5 1]
En lugar de almacenar las tres partes de la transformación compuesta en tres matrices independientes, puede multiplicar A, B y C juntas para obtener una sola matriz de 3×3 que almacena toda la transformación compuesta. Tenemos ABC = D. A continuación, un punto multiplicado por D da el mismo resultado que un punto multiplicado por A, después B y C.
[2 1 1]D = [-2 5 1]
En la ilustración siguiente se muestran las matrices A, B, C y D.
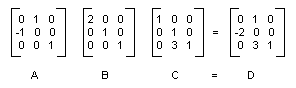
El hecho de que la matriz de una transformación compuesta se pueda formar multiplicando las matrices de transformación individuales significa que cualquier secuencia de transformaciones afines se puede almacenar en un solo objeto Matrix.
Precaución
El orden de una transformación compuesta es importante. En general, girar, luego escalar y después trasladar no es lo mismo que escalar, luego girar y después trasladar. Del mismo modo, el orden de multiplicación de matriz es importante. En general, ABC no es lo mismo que BAC.
La clase Matrix proporciona varios métodos para crear una transformación compuesta: Multiply, Rotate, RotateAt, Scale, Shear y Translate. En el ejemplo siguiente se crea la matriz de una transformación compuesta que gira primero 30 grados y luego se escala por un factor de 2 en la dirección y; por último, se traslada 5 unidades en la dirección x:
Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);
Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)
