Curvas spline cardinales en GDI+
Una curva spline cardinal es una secuencia de curvas individuales unidas para formar una curva mayor. La curva spline se especifica mediante una matriz de puntos y un parámetro de tensión. Una curva spline cardinal pasa sin problemas a través de cada punto de la matriz; no hay esquinas en ángulo ni ningún cambio brusco en la tensión de la curva. En la ilustración siguiente se muestra un conjunto de puntos y una curva spline cardinal que pasa por cada punto del conjunto.
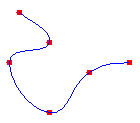
Curvas splines físicas y matemáticas
Una curva spline física es una pieza fina de madera u otro material flexible. Antes de la llegada de curvas spline matemáticas, los diseñadores usaron curvas spline físicas para dibujar las curvas. Un diseñador colocaría la curva spline en un trozo de papel y la anclaría a un conjunto determinado de puntos. Después, podría crear una curva dibujando a lo largo de la spline con un lápiz o un bolígrafo. Un conjunto determinado de puntos podría producir varias de curvas, dependiendo de las propiedades de la curva spline física. Por ejemplo, una curva spline con una alta resistencia al doblado produciría una curva diferente a una curva spline extremadamente flexible.
Las fórmulas de las curvas spline matemáticas se basan en las propiedades de las barras flexibles, por lo que las curvas producidas por curvas spline matemáticas son similares a las curvas que una vez se produjeron mediante curvas spline físicas. Al igual que las curvas spline físicas de diferentes tensiones producirán diferentes curvas a través de un conjunto determinado de puntos, las curvas spline matemáticas con valores diferentes para el parámetro de tensión producirán diferentes curvas a través de un conjunto determinado de puntos. En la ilustración siguiente se muestran cuatro curvas spline cardinales que pasan por el mismo conjunto de puntos. Se muestra la tensión para cada curva spline. Una tensión de 0 corresponde a la tensión física infinita, que fuerza a la curva a tomar el camino más corto (líneas rectas) entre puntos. Una tensión de 1 no corresponde a ninguna tensión física, lo que permite que la curva spline tome el camino de la curva mínima total. Con valores de tensión mayores que 1, la curva se comporta como un muelle comprimido, empujado para tomar un trazado más largo.
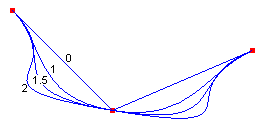
Las cuatro curvas spline de la ilustración anterior comparten la misma línea tangente en el punto inicial. La tangente es la línea dibujada desde el punto inicial hasta el siguiente punto a lo largo de la curva. Del mismo modo, la tangente compartida en el punto final es la línea dibujada desde el punto final hasta el punto anterior de la curva.
Para dibujar una curva spline cardinal, necesita una instancia de la clase Graphics, un Pen y una matriz de objetos Point. La instancia de la clase Graphics proporciona el método DrawCurve, que dibuja la curva spline, y Pen almacena los atributos de la curva spline, como el ancho de línea y el color. La matriz de objetos Point almacena los puntos por los que pasará la curva. En el ejemplo de código siguiente se muestra cómo dibujar una curva spline cardinal que pasa por los puntos de myPointArray. El tercer parámetro es la tensión.
myGraphics.DrawCurve(myPen, myPointArray, 1.5f);
myGraphics.DrawCurve(myPen, myPointArray, 1.5F)
Consulte también
.NET Desktop feedback
