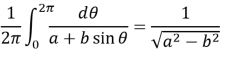Converting Microsoft Equation Editor Objects to OfficeMath
As discussed in the post Editing equations created using the Microsoft Equation Editor, the Microsoft Equation Editor 3.0 (MEE) was removed from Office installations because it has security problems and no maintenance. Microsoft doesn’t have access to the MEE source code and MEE’s author, Design Science, doesn’t maintain it, instead offering the more powerful, upward-compatible MathType program. Provided the MT Extra font is installed, MEE OLE objects display correctly, but they cannot be edited unless the user installs MathType or converts them to Office native math zones (OfficeMath). This post describes the conversion facility that ships with Office 365. The feature sets of MEE, MathType and OfficeMath are compared in the post Equation-Editor OfficeMath Feature Comparison and Other Office Math Editing Facilities. The converter can convert most MEE and MathType OLE objects to OfficeMath. Some equation objects cannot be converted, e.g., long division, since OfficeMath doesn’t have a counterpart. First, let’s see how the converter works in PowerPoint, Excel, and Word, then let’s check out the functions a program can call to perform conversions, and lastly, let’s interpret an MEE “Equation Native” binary data stream. Please let us know your thoughts via Send A Smile with #MEEConverter in the text.
File Format Prerequisite
Conversion to OfficeMath is only enabled for program modes that support the OMML (Office Math Markup Language) file format. If a file is opened in “Compatibility Mode”, equation objects in the file may not be directly convertible to OfficeMath. Word added OMML support in Word 2007 and PowerPoint and Excel added it in Office 2010. The old doc, ppt, and xls file formats do not support OMML. To convert equation objects in such files, first save them as the corresponding docx, pptx, and xlsx files using the Save As menu option. Then you can click on an equation object and get a menu/dialog that offers “Convert Equation to Office Math” and an option to “Apply to all equations”.
Office Equation Object Conversion
PowerPoint displays OLE objects on a slide wherever you put them. The objects are not embedded in the text of text boxes and hence don’t flow with text. For example, if you line up an equation object with text in a text box and change the text size, the text moves, but the equation object doesn’t move since it’s not part of the text. This differs from Word, for which OLE objects are embedded in the text and therefore flow with text changes.
The equation-editor converter converts OLE objects to native math (OfficeMath) text. To put the OfficeMath for a converted object onto a PowerPoint slide, the OfficeMath is stored in its own OfficeArt text box, which has the same dimensions as the original OLE object. People often position a set of equation objects to lay out equations nicely. Ideally all these objects would end up properly aligned in a single text box. But that’s a tricky recognition task and it isn’t handled by the converter. Users may want to do some cutting and pasting to get optimal results. The same approach is used for converting MEE objects in Excel.
In Word, equation objects are embedded in the text and the corresponding OfficeMath text replaces the objects in that text. So, equation conversion in Word doesn’t have object/text alignment problems, although line and page breaks may change due to the use of different fonts. OfficeMath requires a math font for characters supported by a math font, while MEE and MathType use a collection of non-math fonts that can be customized by the user.
Text Size of Converted Equations
The MEE object Equation-Native binary data (described in later sections) includes relative font sizes but doesn’t provide an overall default font size. For example, if you resize an equation object in PowerPoint, the Equation-Native binary data doesn’t change nor do the text sizes in the Windows metafile used to display the object. If the converted math text is too large for its text box, PowerPoint decreases the font size to fit. In any event, the converted math text typically has a different size from that in the original OLE object.
Fixups
There are two kinds of fixups performed by the converter: 1) those handling differences in the math models as described in Integrands, Summands, and Math Function Arguments and Subscript and Superscript Bases, and 2) those dealing with equation object errors that don’t affect the object display significantly but change the display of the converted math text. For example, in OfficeMath, empty numerators, denominators, subscripts, superscripts, etc., display the place-holder character ⬚. Since the OLE objects don’t display such a character, the converter fixes up equations by removing empty subscripts and converting left subscripts with no bases into normal (right) subscripts. Similarly, if a math function name like “min” doesn’t have an argument, the converter treats the function name as ordinary text, rather than as a function-apply object with an empty base. In testing PowerPoint presentations, we found many such errors including an extreme case of an MEE subscript object with a subscript consisting of a “pile” of four empty lines. The converted math text shows a column (equation array) of four ⬚’s although the original object shows nothing. It seems reasonable to have the user delete errors that are that complicated. MEE and MathType use the deprecated codes U+2329 and U+232A for the wide-angle brackets ⟨ (U+27E8) and ⟩ (U+27E9), respectively. The converter replaces the former pair by the latter pair. It also changes the upper limit construction for ≝ into the single character (U+225D).
APIs
Now things get more technical. The converter is implemented as part of RichEdit and uses the same TOM interfaces as the UnicodeMath/LaTeX/speech/braille build up/down facilities. The Office RichEdit dll (riched20.dll) exports three conversion functions: ConvertEquationFromStorage() converts the object given by an IStorage interface, ConvertEquationFromOleStream() converts the object given by the OLESTREAM Get() method (prototype defined in ole2.h), and ConvertEquationFromStdVector() converts the equation binary data in the “Equation Native” stream. These functions don’t call operating-system OLE functions; hence they can be used on all major platforms. The prototypes for the functions are
HRESULT ConvertEquationFromOleStream(
ITextRange2 * prg,
ITextStrings2 * pstrs,
OLESTREAM * poleStream, // OLE stream to read from
BYTE bVersion) // Design Science MathType version #
HRESULT ConvertEquationFromStorage(
ITextRange2 * prg, // Range for inserting result
ITextStrings2 * pstrs, // Rich-text string stack
IStorage * pstg) // IStorage for OLE math object
HRESULT ConvertEquationFromStdVector(
ITextRange2 * prg,
ITextStrings2 * pstrs,
std::vector<BYTE> & EquationNative, // "Equation Native" binary stream
BYTE bVersion) // Design Science version # (3-EE3, 5-MathType)
The interface ITextStrings2 is defined in the Office tom.h (eventually it’ll be in the Windows tom.h) and derives from ITextStrings. It adds the method
ITextStrings2::Rotate(LONG iString)
ITextStrings2::Rotate(-2) reorders the Design Science N-ary arguments to put the naryand (integrand, summand, …) third instead of first. ITextStrings2::Rotate(-1) is the same as ITextStrings::Swap() and swaps the top two strings. If the Type argument of ITextStrings::EncodeFunction() has the tomTeXStyleIsTextColor flag set, the TeXStyle argument has the text color instead of the TeXStyle. The TeXStyle isn't used by the converter since it’s implied by context (although it is stored in the OLE object binary data).
ConvertEquationFromStorage() calls IStorage::OpenStream(L”Equation Native”, …) to retrieve the Design Science OLE object’s “Equation Native” stream and then calls the converter to create the corresponding native math zones.
ConvertEquationFromOleStream() reads a Design Science object's compound file format, defragments it, retrieves the “Equation Native” stream, and calls the converter to create the corresponding math zones.
ConvertEquationFromStdVector() converts the "Equation Native" binary stream to a built-up Office math zone. This function is handy for unit tests. Enter with the EquationNative std::vector<BYTE> starting with the byte following the two "Equation Native" stream headers. The “Equation Native” binary format is illustrated in the next section.
Equation Native Stream
The Design Science OLE object "Equation Native" stream contains the MTEF binary data for a MathType or MEE object. The MTEF data consists of a 28-byte equation-OLE header, a version header (5 bytes for MEE and 12 bytes for MathType) followed by the records for the equation. Container records (rcdLINE, rcdTMPL, rcdPILE, rcdMATRIX) can contain other records including themselves and are terminated by the end record rcdEND. For full documentation, see MathType's Equation Format (MTEF) in the MathType SDK (https://www.dessci.com/en/reference/sdk/).
The following table illustrates the Equation Editor 3.0 binary records for the equation
The two headers in the Equation-Native stream are omitted. Putting the binary into a std::vector<BYTE> and passing it to ConvertEquationFromStdVector(), you insert this equation into the text. Be sure to convert the ASCII hex characters to binary, two per byte with no intervening spaces. Note that the integrand precedes the integral limits. In OfficeMath, the integrand follows the limits, hence the need for ITextStrings2::Rotate().
| binary | meaning |
|
|
Comments
- Anonymous
September 03, 2018
Informative