Exercise - Create quantum entanglement with Q#

Completed

In the previous unit, you learned about the concept of quantum entanglement and Bell states.

Now, let's create quantum entanglement using Q# and the Azure Quantum Development Kit. To create entanglement, you need to apply two quantum operations: the Hadamard gate and the Controlled-NOT (CNOT) gate.

The Controlled-NOT (CNOT) operation

When two qubits are entangled, the state of one qubit is dependent on the state of the other qubit. Therefore, to entangle two qubits you need an operation that acts on both qubits at the same time. This is called a multiqubit operation.

To create quantum entanglement, you need the multiqubit CNOT operation, which stands for Controlled-NOT. This operation takes two qubits as input, one acts as control qubit and the other is the target qubit. The CNOT operation flips the state of the second qubit (the target qubit) if, and only if, the state of the first qubit (the control qubit) is $|1\rangle$.

Input	Output
$\ket{00}$	$\ket{00}$
$\ket{01}$	$\ket{01}$
$\ket{10}$	$\ket{11}$
$\ket{11}$	$\ket{10}$

In Q#, the CNOT operation acts on an array of two qubits, and it flips the second qubit if the first qubit is One.

Entanglement with a CNOT operation

By applying the Hadamard, H, operation and the Controlled-NOT, CNOT, operation, you can transform two qubits in the state $|00\rangle$ to the Bell state $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.

Here's how it works:

1. Take two qubits in the state $|00\rangle$. The first qubit is the control qubit and the second qubit is the target qubit.

2. Create a superposition state only in the control qubit by applying $H$.

   $$H |0_c\rangle= \frac{1}{\sqrt{2}}(|0_c\rangle+|1_c\rangle)$$

   Tip

   The subscripts ${}_c$ and ${}_t$ specify the control and target qubits.

3. Apply the $CNOT$ operator to the control qubit, which is in a superposition state, and the target qubit, which is in the state $|0_t\rangle$.

   $$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c}+\ket{1_c})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}+|\ket{1_c 0_t})= $$ $$ =\frac{1}{\sqrt2}(CNOT \ket{0_c 0_t} + CNOT \ket{1_c 0_t})= $$ $$= \frac{1}{\sqrt2}(\ket{0_c 0_t}+\ket{1_c 1_t})$$

Create a new Q# file

1. Open Visual Studio Code.
2. Select File > New Text File and save it as Main.qs.
3. Select View -> Command Palette and type Q#: Set the Azure Quantum QIR target profile. Press Enter.
4. Select Q#: Unrestricted.

Create the Bell state $\ket{\phi^+}$

Let's start by creating the Bell state $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.

1. First, you need to import the Microsoft.Quantum.Diagnostics namespace from the Standard library, which contains the DumpMachine function. This function shows the current state of the qubits. Copy and paste the following Q# code into Main.qs file.

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   

   Tip

   You can also import the Standard library by substituting Microsoft.Quantum with Std. For example, import Std.Diagnostics.* is equivalent to import Microsoft.Quantum.Diagnostics.*.

2. Create the Main operation that returns two Result type values, which are the measurement results of the qubits.

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
       // Your code goes here
   }
   

3. Inside the Main operation, you allocate two qubits, q1 and q2, that will be entangled.

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
       use (q1, q2) = (Qubit(), Qubit());
   }
   

4. Apply the Hadamard gate, H, to the first qubit, q1, to put it in a superposition state. Then, entangle the two qubits using the CNOT operation.

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
       use (q1, q2) = (Qubit(), Qubit());
   
       H(q1);
       CNOT(q1, q2);
   }
   

5. Use the DumpMachine function to display the current state of the qubits. This is not the same as measuring the qubits.

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
       use (q1, q2) = (Qubit(), Qubit());
   
       H(q1);
       CNOT(q1, q2);
   
       DumpMachine();
   }
   

6. Measure the qubits using the M operation and store the results in m1 and m2. Then, use the Reset operation to reset the qubits. In Q#, you must always reset the qubits to the $|0\rangle$ state.

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
   
       use (q1, q2) = (Qubit(), Qubit());
   
       H(q1);
       CNOT(q1, q2);
       DumpMachine();
   
       let (m1, m2) = (M(q1), M(q2));
       Reset(q1);
       Reset(q2);
   
   }
   

7. Finally, return the measurement results of the qubits with the return statement. Your Main.qs file should look like this:

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
       use (q1, q2) = (Qubit(), Qubit());
   
       H(q1);
       CNOT(q1, q2);
   
       DumpMachine();
   
       let (m1, m2) = (M(q1), M(q2));
       Reset(q1);
       Reset(q2);
   
       return (m1, m2);
   }
   

8. To run your program on the built-in simulator, click on Run above the Main operation or press Ctrl+F5. Your output will appear in the debug console.

9. The measurement outcomes are correlated, so at the end of the program, you get a result of (Zero, Zero) or (One, One) with equal probability.

10. You can visualize the circuit diagram by clicking on Circuit from the list of commands above the Main operation. The circuit diagram shows the Hadamard gate applied to the first qubit and the CNOT gate applied to both qubits.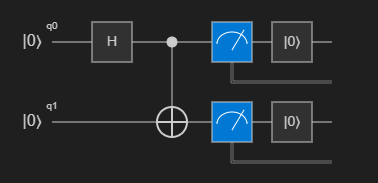

    

Create other Bell states

To create other Bell states, you need to apply additional Pauli $X$ and $Z$ operations to the qubits.

For example, to create the Bell state $\ket{\phi^-}=\frac1{\sqrt2}(|00\rangle-|11\rangle)$, you can apply the Pauli $Z$ operation to the control qubit after applying the Hadamard gate. The $Z$ operation flips the state $\ket{+}$ to $\ket{-}$.

Tip

The states $\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ and $\frac{1}{\sqrt{2}}(|0\rangle -|1\rangle)$ are also known as $\ket{+}$ and $\ket{-}$, respectively.

Here's how it works:

1. Take two qubits in the state $|00\rangle$.

2. Create a superposition state only in the control qubit by applying $H$.

   $$H |0_c\rangle= \frac{1}{\sqrt{2}}(|0_c\rangle+|1_c\rangle) = \ket{+}_c$$

3. Apply the $Z$ operation to the control qubit.

   $$Z \frac{1}{\sqrt{2}}(|0_c\rangle+|1_c\rangle)= \frac{1}{\sqrt{2}}(|0_c\rangle-|1_c\rangle)= \ket{-}_c$$

4. Apply the $CNOT$ operator to the control qubit and the target qubit, which is in the state $|0_t\rangle$.

   $$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c}-\ket{1_c})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}-|\ket{1_c 0_t})= $$ $$ =\frac{1}{\sqrt2}(CNOT \ket{0_c 0_t} - CNOT \ket{1_c 0_t})= $$ $$= \frac{1}{\sqrt2}(\ket{0_c 0_t}-\ket{1_c 1_t})$$

Similarly, Bell states $\ket{\psi^+}$ and $\ket{\psi^-}$ can be created by applying the Pauli $X$ and $Z$ operations to the qubits.

• The Bell state $\ket{\psi^+}=\frac1{\sqrt2}(|01\rangle+|10\rangle)$ can be created by applying the Pauli $X$ operation to the target qubit after applying the Hadamard gate.
• The Bell state $\ket{\psi^-}=\frac1{\sqrt2}(|01\rangle-|10\rangle)$ can be created by applying the Pauli $Z$ to the control qubit and the Pauli $X$ to the target qubit after applying the Hadamard gate.

Create the Bell state $\ket{\phi^-}$ in Q#

1. Modify the Q# code to create the Bell state $\ket{\phi^-}$. Your Main.qs file should look like this:

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
       use (q1, q2) = (Qubit(), Qubit());
   
       H(q1);
       Z(q1); // Apply the Pauli Z operation to the control qubit
       CNOT(q1, q2);
   
       DumpMachine();
   
       let (m1, m2) = (M(q1), M(q2));
       Reset(q1);
       Reset(q2);
   
       return (m1, m2);
   }
   

2. To run your program on the built-in simulator, click on Run above the Main operation or press Ctrl+F5. Your output will appear in the debug console.

3. You can visualize the circuit diagram by clicking on Circuit from the list of commands above the Main operation. The circuit diagram shows the Hadamard gate applied to the first qubit, the Pauli $Z$ gate applied to the first qubit, and the CNOT gate applied to both qubits.

In the next unit, you'll learn how to use entanglement to teleport quantum information.