IIR Filter

Article
05/06/2019

Important

Support for Machine Learning Studio (classic) will end on 31 August 2024. We recommend you transition to Azure Machine Learning by that date.

Beginning 1 December 2021, you will not be able to create new Machine Learning Studio (classic) resources. Through 31 August 2024, you can continue to use the existing Machine Learning Studio (classic) resources.

See information on moving machine learning projects from ML Studio (classic) to Azure Machine Learning.
Learn more about Azure Machine Learning.

ML Studio (classic) documentation is being retired and may not be updated in the future.

Creates an infinite impulse response filter for signal processing

Category: Data Transformation / Filter

Note

Applies to: Machine Learning Studio (classic) only

Similar drag-and-drop modules are available in Azure Machine Learning designer.

Module overview

This article describes how to use the IIR Filter module in Machine Learning Studio (classic), to create an infinite impulse response (IIR) filter.

Filters are an important tool in digital signal processing, and are used to improve the results of image or voice recognition. In general, a filter is a transfer function that takes an input signal and creates an output signal based on the filter characteristics. For more general information about the user of filters in digital signal processing, see Filter.

An IIR filter is a particular type of filter; typical uses of an IIR filter would be to simplify cyclical data that includes random noise over a steadily increasing or decreasing trend. The IIR filter you cretae with this module defines a set of constants (or coefficients) that alter the signal that is passed through. The word infinite in the name refers to the feedback between the outputs and the series values.

After you have defined a filter that meets your needs, you can apply the filter to data by connecting a dataset and the filter to the Apply Filter module.

Tip

A filter is a transfer function that takes an input signal and creates an output signal based on the filter characteristics. For more general information about the user of filters in digital signal processing, see Filter.

After you have defined a filter that meets your needs, you can apply the filter to data by connecting a dataset and the filter to the Apply Filter module.

Tip

Need to filter data from a dataset or remove missing values? Use these modules instead:

Clean Missing Data: Use this module to remove missing values or replace missing values with placeholders.
Partition and Sample: Use this module to divide or filter your dataset by criteria such as a range of dates, a specific value, or regular expressions.
Clip Values: Use this module to set a range and keep only the values within that range.

How to configure IIR Filter

Add the IIR Filter module to your experiment. You can find this module under Data Transformation, in the Filter category.
For Order, type an integer value that defines the number of active elements used to affect the filter's response. The order of the filter represents the length of the filter window.

For an IIR filter, the minimum order is 4.
For Filter kind, choose the algorithm that is used to compute filter coefficients. The filter kind designates the mathematical transfer function that controls frequency response and frequency suppression. Machine Learning supports these kinds of filters commonly used in digital signal processing:

Butterworth: A Butterworth filter is also called a maximally flat magnitude filter because it constrains the response (change in signal) in the passband and the stopband.

Chebyshev Type 1: Chebyshev filters are intended to minimize the errors between the idealized and the actual filter characteristics over the range of the filter. Type 1 Chebyshev filters leave more ripple in the passband.

Chebyshev Type 2: Type 2 Chebyshev filters have the same general characteristics as Type 1 Chebyshev filters, but they leave more ripple in the stopband.
For Filter type, select an option that defines how the filter will affect the values in the input signal. You can specify that the filter exclude values above or below a cutoff point, or specify that the filter either reject or pass through values in a specified frequency range.

LowPass: Allows low frequency values (below the cutoff value) to pass and attenuates other values.

HighPass: Allows high frequency values (above the cutoff value) to pass and attenuates other values.

Bandpass: Allows signals in the range that is specified by the low and high cutoff values to pass and attenuates other values.

BandStop: Allows signals outside the range specified by the low and high cutoff values to pass and attenuates values within the range.
Specify the high or low cutoff values, or both, as a value between 0 and 1, representing a normalized frequency. For High cutoff, type a value that represents the upper frequency boundary. For Low cutoff, type a value that represents the lower frequency boundary.
For Ripple, specify the amount of ripple to tolerate when you define your filter. Ripple refers to a small variation that occurs periodically. Ripple is usually considered an unwanted effect, but you can compensate for ripple by adjusting other filter parameters, such as the filter length. Not all filters produce ripple.
Add the Apply Filter module to your experiment, and connect the filter you designed, and the dataset containg the values you want to modify.

Use the column selector to specify which columns of the dataset to which the filter should be applied. By default, the Apply Filter module will use the filter for all selected numeric columns.
Run the experiment to apply the transformation.

Note

The IIR Filter module does not provide the option to create an indicator column. Column values are always transformed in place.

Examples

For examples of how filters are used in machine learning, see this experiment in the Azure AI Gallery:

Filters: This experiment demonstrates all filter types, using an engineered waveform dataset.

Technical Notes

This section contains implementation details, tips, and answers to frequently asked questions.

Implementation details

An IIR filter returns feed forward and feed backward coefficients, which are represented by way of a transfer function. Here is an example representation:

transfer function for IIR filters

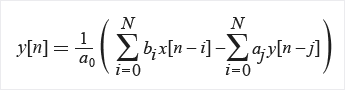
Where:

N: filter order
bi: feed forward filter coefficients
ai: feed backward filter coefficients
x[n]: the input signal
y[n]: the output signal

Module parameters

Name	Range	Type	Default	Description
Order	[4;13]	Integer	5	Specify the filter order
Filter kind	Any	IIRFilterKind		Select the kind of IIR filter to create
Filter type	Any	FilterType		Select the filter band type
Low cutoff	[double.Epsilon;.9999999]	Float	0.3	Set the low cutoff value
High cutoff	[double.Epsilon;.9999999]	Float	0.7	Set the high cutoff value
Ripple	>=0.0	Float	0.5	Specify the amount of ripple in the filter

Output

Name	Type	Description
Filter	IFilter interface	Filter implementation

Exceptions

Exception	Description
NotInRangeValue	Exception occurs if parameter is not in range.

For a list of errors specific to Studio (classic) modules, see Machine Learning Error codes.

For a list of API exceptions, see Machine Learning REST API Error Codes.

Share via